разное к тоэ / РГР 222
.docСАРАТОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра «Электротехника и электроника»
Расчетная работа №2
«Электрические цепи синусоидального тока»
Выполнил: студент 2 курса
Группы РТС-22 Харитонова М.А.
Проверил: Осипова С.В.
Саратов 2006г.
Номер схемы -6, числовой вариант – 2.
С
L2
Числовые данные параметров схемы:
|
f, Гц |
E1, B |
E2, B |
α, рад |
R1, Ом |
R2, Ом |
R3, Ом |
L1, мГн |
L2, мГн |
L3, мГн |
С1, мкФ |
С2, мкФ |
С3, мкФ |
К12 |
К23 |
К31 |
|
50 |
100 |
200 |
|
6 |
4 |
4 |
30 |
50 |
20 |
200 |
300 |
300 |
0,6 |
0,8 |
0,0 |
Задания.
Ι. Считая, что индуктивная связь отсутствует (М=0):
-
На основании законов Кирхгофа составить в общем виде систему уравнений для расчета токов во всех ветвях цепи, записав ее:
а) в дифференциальной форме;
б) в символической форме.
-
Методом контурных токов рассчитать токи во всех ветвях схемы.
-
Проверить правильность полученных в пункте 2 значений токов, используя законы Кирхгофа.
-
Построить топографическую диаграмму цепи, совмещенную с векторной диаграммой токов (при построении потенциал точки а принять равным нулю, точка а указана на схеме).
-
Вычислить показания ваттметра по данным пунктов 2 и 4, пользуясь:
а) формулой расчета активной мощности
однофазного тока
;
б) формулой расчета комплексной мощности.
-
Написать выражения для
,
,
.
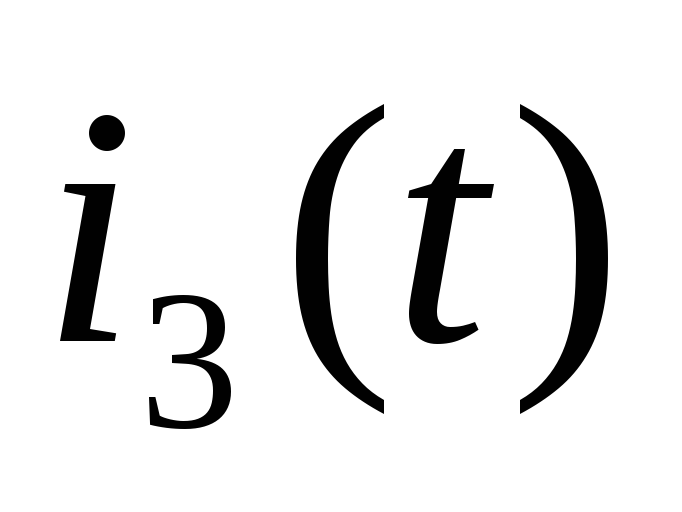II. Учитывая взаимную индуктивность катушек, составить на основании законов
Кирхгофа систему уравнений (в общем виде и с числовыми коэффициентами)
для расчета токов во всех ветвях цепи, записав ее:
а) в дифференциальной форме;
б) в символической форме.
Примечание: в расчетах допускается погрешность не более 1,5%.
Часть первая: Задание №1.
L2
C2
Начнем с определения амплитудного значения ЭДС синусоидальных токов:
B,
B.
Определим угловую частоту:
рад/с.
Запишем Е1 и Е2 в комплексной форме:
-
тригонометрическая форма:
В;
В.
-
показательная форма:
В;
В.
По первому закону Кирхгофа составляю n–1 = 2–1 = 1 уравнение:
-
в дифференциальной форме:
1:
;
-
в символической форме:
1:
.
По второму закону Кирхгофа составляю m–n+1 = 3–2+1 = 2 уравнения:
-
в дифференциальной форме:
1:
В
2:
В
-
в символической форме:
1:
В
2:
В
Задание №2.
Метод контурных токов является одним из основных методов расчета сложных электрических цепей, которым широко пользуются на практике. Этот метод заключается в том, что вместо токов в ветвях определяются на основании второго закона Кирхгофа так называемые контурные токи, замыкающиеся в контурах.
Данная цепь содержит 3 ветви. Заменим все сопротивления в каждой ветви на эквивалентные им комплексные сопротивления:
Таким образом, исходную схему можно изобразить следующим образом:
Выбираем два независимых
контура.
Задаемся положительными направлениями
обхода контуров так, как указано на схеме.
На основании второго закона Кирхгофа составляем для двух выбранных независимых контуров систему уравнений:
Решаем эту систему уравнений из двух уравнений с двумя неизвестными методом Крамер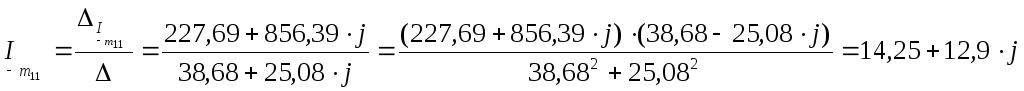а:
А,
А.
Теперь по вычисленным контурным токам
определим необходимые токи ветвей
,
,
:
-
ток первой ветви, как видно на схеме, равен контурному току
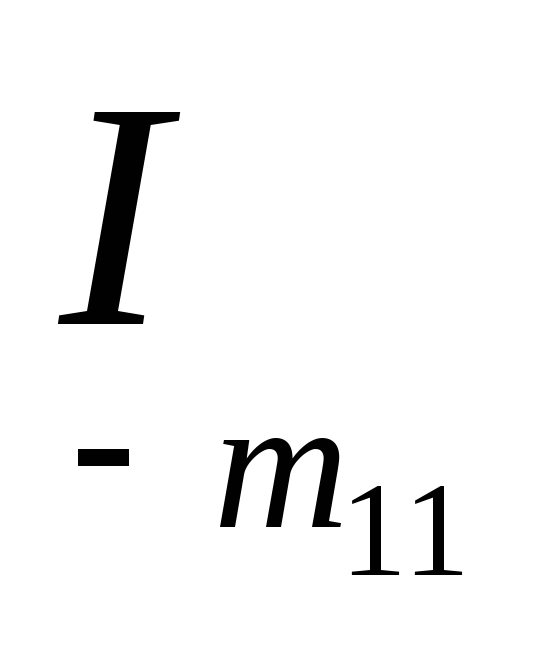(первая
ветвь входит только в контур тока
):
А;
-
ток второй ветви, по аналогии, равен контурному току
:
А;
-
ток третьей ветви равен сумме контурных токов
,
так как оба контурных тока имеют
одинаковые направления и проходят
через третью ветвь:
+
=
А.
Задание №3.
Правильность найденных в предыдущем пункте токов проверяется с помощью второго закона Кирхгофа.
В пункте 1 мы уже составили систему
уравнений для двух выбранных независимых
контуров. Подставим вычисленные токи
,
,
в данную систему. Допустимая погрешность
μ ≤ 1,5%.
1:
В
2:
В
Расчет будем вести в алгебраической
форме записи комплексного числа, поэтому
переведем
и
в
алгебраическую форму:
В,
В.
Таким образом, мы имеем:
1:
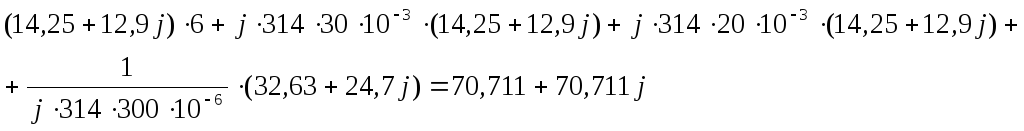
В
2:
В
Задание №4.
Топографическая (потенциальная) диаграмма – это диаграмма комплексных потенциалов, причем каждой ее точке соответствует определенная точка в электрической схеме.
Топографическая диаграмма позволяет весьма просто находить напряжения между любыми двумя точками цепи: действующее значение и фаза искомого напряжения определяются прямой, соединяющей соответствующие точки топографической диаграммы.
Из условия потенциал точки а, указанной в схеме, принять равным нулю. При определении потенциалов точек следует помнить, что в пассивном элементе ток направлен от точки с большим потенциалом к точке с меньшим потенциалом. Имеем следующее:
В
В
В
В
В
В
В
В
В
В
В
