разное к тоэ / Курсовой1

Министерство Образования Российской Федерации

Саратовский государственный технический университет

Балаковский институт техники, технологии и управления

Расчетно-графическая работа по предмету:

«Теоретические основы электротехники»

Выполнил:

студент группы УИТ-32

Бнатов М.А.

Проверил:

Зайцев А.В.

Балаково 2005

Дано:

R₁= 4 Ом Е₁= 25 В

R₂= 11 Ом Е₂= 4,5 В

R₃= 5 Ом I_к1= 0 А

R₄= 12 Ом I_к2= 0,5 А

R₅= 7 Ом

R₆= 8 Ом

Нулевой потенциал – потенциал узла а.

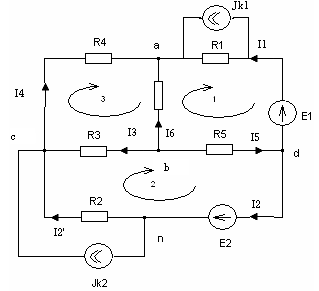
I. Проводим анализ схемы – число узлов (n=5), источник тока J_k2 = 0, поэтому его не рисуем; число ветвей (m=8), число ветвей с источником тока (m_J=1).

Произвольно расставляются действительные токи в ветвях.

1. По первому закону Кирхгоффа составляется n-1 уравнение (n- число узлов).

Узел а:

I₄+ I₁+ I₆ =0

Узел b:

I₃- I₄+ I₂+ J_k2 =0

Узел d:

I₅- I₁- I₂ =0

Узел c:

-I₃- I₅- I₆ =0

2. По второму закону Кирхгоффа составляется m-m_J –(n-1) уравнения.

Контур 1:

I₆· R₆- I₁· R₁- I₅· R₅= -E₁;

Контур 2:

I₅· R₅+ I₂· R₂- I₃· R₃= E₂;

Контур 3:

I₄· R₄- I₆· R₆+ I₃· R₃= 0.

II. Метод контурных токов (МКТ) – заключается в определении контурных токов и расчете действительных токов в ветвях через известные контурные токи. Количество контурных токов всегда равно числу уравнений, составленных по второму закону Кирхгоффа.

I₁= - I₂₂; I₁= 1,6126

I₂= I₃₃; I₂= -0,1758

I₃= I₁₁- I₃₃; I₃= -0,3754

I₄= I₁₁; I₄= -0,5512

I₅= I₃₃ - I₂₂; I₅= 1,4368

I₆= I₂₂ – I₁₁. I₆= -1,0614

I₁₁(R₃+ R₄+ R₆) - I₂₂· R₆ - I₃₃· R₅= 0;

-I₁₁·R₆ + I₂₂(R₁+ R₅+ R₆) - I₃₃· R₅= - E₁;

-I₁₁·R₃ - I₂₂· R₅ + I₃₃(R₃+ R₂+ R₅)= E₂+ E_J.

I₁₁= -0,5512; I₂₂= -1,6126; I₃₃= -0,1758.

Проверка:

-1,0614· 8- 1,6126· 4- 1,4368· 7= -25 -24,9992≈ -25;

-0,5512·12+ 1,0614· 8- 0,3754· 5= 0 -0,0002≈ 0.

III. Метод узловых потенциалов (МУП) – заключается в определении потенциалов узлов схемы и расчете токов по закону Ома для активного участка цепи. (Предварительно преобразуем источник тока в источник ЭДС).

φ_а=0.

I₁= ;

I₂= ;

I₃= ;

I₄= ;

I₅= ;

I₆= .

φ_b(g₃+ g₅+ g₆)- φ_c· g₃- φ_d· g₅= 0;

-φ_b·g₃+ φ_c(g₂+ g₃+ g₄) - φ_d· g₂= (E_J+ E₂) · g₂;

-φ_b·g₅- φ_c· g₂+ φ_d(g₁+ g₂+ g₅) = -E₁· g₁- (E_J+ E₂) · g₂;

φ_b= -8,4912; φ_с= -6,6144; φ_d= -18.5496.

IV. Баланс мощностей. В любой конкретный момент времени мощность, отдаваемая источником тока равна мощности, которая выделяется на приемниках электрической энергии (резисторах).

Р_ист.= Р_пр.

Р_пр. =

Р_ист.=

38,553≈38,557

V. Два узла: b и с.

I_A=-I_НН; I_A= -0,09;

I_К=I_НН – I_СС; I_К= 0,364;

I_М= I_СС. I_М= 0,454.

I_НН(R₃+ R₄+ R₆)- I_СС· R₃= 0;

-I_НН· R₃ + I_СС(R₂+ R₃+ R₅) = E₂+ E_J.

I_НН=0.09

I_CC=0.454

Второй закон Кирхгоффа:

По первому контуру:

-U_xx- I_М· R₅+ I_A· R₆= -E₁;

U_xx= E₁- I_М· R₅+ I_A· R₆;

U_xx= 25- 0.454 7- 0.09· 8= 21.102 В.

Определяем входное сопротивление схемы относительно зажимов выделенной ветви.

Треугольник сопротивлений R₃, R₄, R₆ преобразуем в эквивалентную звезду.

;

;

.

r_вх=R_Э

VII. Потенциальная диаграмма.

φ_а= 0;

φ_l= φ_а+R₁·I₁= 6.4504;

φ_d= φ_c- E₁= 18.5496;

φ_f= φ_d+ E₂= -14.0496;

φ_k= φ_f – R₂·I₂= -12.1158;

φ_c= φ_k+ E_J= -6.6158;

φ_а= φ_c – R₄·I₄= -6.6158+ 6.6144≈0.