разное к тоэ / Курсовая работа по ТОЭ

Задача №1 Дана электрическая цепь, в которой происходит коммутация. В цепи требуется постоянная ЭДС. Требуется определить закон изменения во времени тока после коммутации в первой из ветвей схемы или напряжения на коком либо элементе или между заданными точками схемы. Задачу следует решать двумя методами: классическим и операторным. На основании полученного аналитического выражения требуется построить график изменения искомой величины в функции времени на интервале от t=0 до . Здесь - меньший по модулю корень характеристического уравнения.

E = 50 B;

L = 1 мГн;

C = 1500 мкФ;

R₁ = 2 Ом;

R₂ = 13 Ом;

R₃ = 2 Ом;

R₄ = 3 Ом.

i-?

i₁ L R₁ R₃

i

E C

R₂ R₄

I. Классический метод

1. Для темы до коммутационного режима определяем ток через индуктивность и напряжения на емкости. Составляем схему замещения:

i₁(0_ ) L R₁ R₃

E U_c(0_ )

R₂ R₄

2. Рассчитываем принужденные составляющие искомой величины и принужденное составляющее тока через индуктивность и напряжения на емкости цепи после коммутации:

i_1пр L R₁ R₃

E U_{c пр}

i_пр

3. Находим значения свободных составляющих токов через индуктивность и напряжения на емкости:

4. Составляем характеристическое уравнение:

Lp

R₁ R₃₄

Z(p)

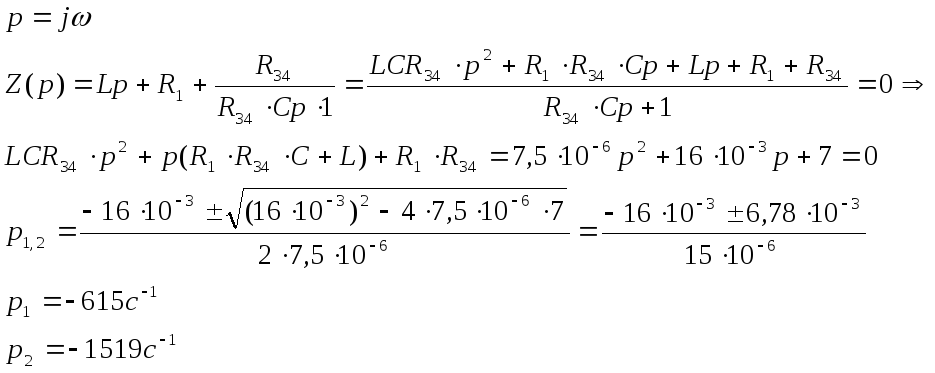
5. Решение для свободной составляющей искомой величины имеет вид:

(1)

продифференцируем решения:

(2)

при t=0

(3)

Для определения коэффициентов А₁, А₂ составим систему уравнений по закону Кирхгофа:

i_{1 св}(0) L R₁ R₃₄

i_св(0) i_{2 св}(0)

U_{c св}(0) 1/Cp

(4)

(5)

(6)

(7)

(8)

продифференцируем (4) и (7):

(9)

(10)

Из (7):

Из (4):

Из (8):

Из (10):

Из (5):

Из (9):

Подставим найденные значения в систему (3):

6. Общее решение искомой величины равно:

, т.к. i_пр=0

II. Операторный метод

1. Составляем операторную схему замещения для свободно составляющих токов и напряжений:

L p R₁ R₃₄

I_св(p) I_{2 св}(p)

I_{1 св}(p) LI_{1 св(0)} 1/Cp

U_{c св}(0)/p

2. Определим изображение искомой величины МКТ.

Составляем уравнение по МКТ:

Передем от изображения к оригиналу:

III. Построим график i(t).

В интервале t от 0 до ,

t, c	0		2	3	4
i, A	0	10,2	4,6	1,8	0,7

Задача №2 Дана электрическая схема, на входе, которой действует напряжение, изменяющиеся во времени по заданному закону U₁ (t). Определить закон изменения во времени тока впервой из ветвей схемы или напряжения на заданном участке схемы. Задачу решить с помощью интеграла Дюамеля. Искомую величину определить для всех интегралов времени.

R

i₂

U_вх C

R

U_вх

U_вх=2A-kt

A

t

t₁ t₂

1. На вход схемы подается единичная функция и рассчитывается ток i_c (t).

Ток i_c (t) будем рассчитывать как операторный метод, схема до подачи функции Хевисайда была отключена, поэтому начальные условия вихревые.

U_c (0_-)=U_c (0₊)=0

Составляем операторную схему замещения:

R a

I₂(p)

1/p 1/Cp

U_a(p) R

b

Рассчитывается сопротивление параллельного участка:

Общее сопротивление:

Находим I_c (p):

Переход от изображения к оригиналу. Решаем уравнение:

выписываем N(p)=C; N(p₁)=C

выписываем M(p)=RCp+2; (p)=RC; (p₁)=RC

Так как на вход подавалось функция Хевисайда, то ток равен:

Таким образом

2. Рассчитаем с помощью интеграла Дюамеля ток i₂(t) для различных промежуток времени. Для каждого интервала времени записывается свой интеграл Дюамеля. На заданном входном напряжении можно определить при интервала.

U_вх

U_вх=2A-kt

U_вх2=A

А

0

t₁ t₂

Записываем интеграл Дюамеля для интервала времени от 0 до t₁. этот интеграл Дюамеля справедлив для любого конкретного момента времени t лежащего в пределах от 0 до t₁.

U(0)-скачок напряжения в момент равен нулю.

С учетом обозначений интеграл Дюамеля записывается в виде:

Записываем второй интеграл Дюамеля, который работает в пределах от t₁ до t₂. можно вычислить ток, задав времени t малое в пределах от t₁ до t₂.

физически это означает, что скачка нет

После подстановки данных интеграл Дюамеля для второго участка имеет вид:

Записываем третий интеграл Дюамеля, работающий в пределах от t₂ до :

После замены:

3. Рассчитаем спектр прямоугольного импульса.

U(t)

U₀

t

Находим центральную плотность:

Переходим к модулю:

Таким образом

Построим частотную характеристику: