экзамен / 8

для составления характеристического уравнения в нем все производные от искомой величины заменяются корнем p в соответствующей степени, а сама искомая функция заменяется единицей:

.

Метод входного сопротивления (входной проводимости)

• Составляем цепь, соответствующую свободному режиму (для этого удаляем все источники электрической энергии: источники ЭДС замыкаем накоротко, ветви с источниками тока размыкаем).

• Размыкаем цепь в произвольном месте и относительно точек разрыва записываем входное комплексное сопротивление 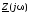, при этом комплекс емкостного сопротивления , а индуктивного .

• В полученном выражении повсеместно величину заменяем корнем p и приравниваем выражение к нулю.

• Уравнение является характеристическим уравнением.

Следует отметить, что для цепей, содержащих большое количество параллельных ветвей, удобно пользоваться методом входной проводимости. Метод состоит в том, что записывается эквивалентная комплексная проводимость между двумя произвольными узлами послекоммутационной цепи с отключёнными источниками. Далее, как и в предыдущем случае, j заменяется на р и решается уравнение .

Метод главного определителя

• Составляем цепь, соответствующую свободному режиму.

• Выбираем независимые контуры и задаем направление их контурных токов.

• Составляем главный определитель , состоящий из собственных и общих контурных комплексных сопротивлений.

• Повсеместно заменяем на p и приравниваем нулю.

• Уравнение – характеристическое уравнение

.

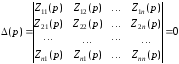R₃

Рассмотрим применение описанных способов определения корней характеристического уравнения на примере цепи второго порядка(рис. 4.4).

Метод входного сопротивления. Разорвём ветвь в цепи (рис. 4.4), содержащую емкость, и относительно точек разрыва запишем входное сопротивление

Тогда характеристическое уравнение для указанной цепи

Метод главного определителя. Выберем независимые контуры и укажем направление их обхода (рис. 4.4). Составим главный определитель, заменяя на p

.

Как видно, оба метода приводят к одному характеристическому уравнению.

Существует еще один способ, основанный на определении постоянной времени, применимый только для цепей I порядка.

Постоянной времени  цепи называют промежуток времени, за который искомая величина изменится в е раз. Время переходного процесса прямо пропорционально  и приближённо равно:

. (4.7)

Для устойчивых цепей (цепей, в которых соблюдается условие ) корни характеристического уравнения должны быть отрицательными или иметь отрицательную действительную часть. Постоянная времени для цепей I порядка связана с корнем характеристического уравнения:

. (4.8)

Причём для цепей, содержащих ёмкость, –  = R_эС, а для цепей, содержащих индуктивность, – =L/R_э, где R_э – эквивалентное сопротивление послекоммутационной цепи, вычисленное относительно зажимов единственного реактивного элемента (накопителя энергии) при удаленных источниках.