4.2.6.1. Разряд емкости на цепь rl

1. Независимые начальные условия для рассматриваемой цепи (рис. 4.15):

2. Дифференциальное уравнение цепи и корни характеристического уравнения:

;

.

Характеристическое уравнение

или . (4.11)

Корни характеристического уравнения

. (4.12)

3. Полное решение . Вид свободной составляющей и характер переходного процесса будут определяться тем, какими числами будут корни характеристического уравнения. Это зависит от соотношения между параметрами цепи, в частности, от подкоренного выражения в уравнении (4.12). Здесь возможны три варианта:

1. , где  – волновое сопротивление контура, т.е. для низкодобротных контуров Q < 0,5. При этом корни p₁ и p₂ – вещественные отрицательные разные.

2. или Q = 0,5: корни p₁ = p₂ – вещественные отрицательные равные

3. или Q > 0,5: корни p₁ и p₂ – комплексные сопряженные.

В первых двух случаях переходный процесс носит апериодический характер (напряжение на емкости u_C монотонно затухает до нуля, не меняя своей полярности); в третьем случае процесс разряда – колебательный.

. Апериодический емкости на цепь RL

Рассмотрим случай, когда p_1,2 – действительные и отрицательные, т.е. . В этом случае переходный процесс называетсяапериодическим и вид полного решения следующий:

Найдем постоянные интегрирования А₁ и А₂:

;

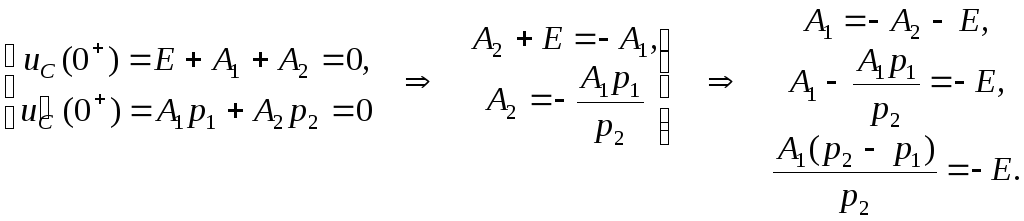
; аналогично: .

Таким образом, искомое имеет вид:

.

; .

Качественно изобразим график (рис. 4.15).

Рассмотрим начальные значения:

Получим функцию изменения тока в цепи:

.

С учетом того, что по теореме Виета ,

.

Для построения графика (рис. 4.16) проведем аналогичные изложенным выше исследования. Поскольку , первая экспонента имеет большую постоянную времени и обращается в нуль за больший промежуток времени. Так как, , , тогда

Получим функцию изменения напряжения на индуктивности

.

С учетом сказанного выше, exp1 находится в нижней полуплоскости и имеет большую постоянную времени, а exp2 находится в верхней полуплоскости и устремляется к нулю за меньший промежуток времени (рис. 4.17).

Начальные условия определяются следующим образом . Поскольку, модулиexp1, 2 отличаются на E, причем exp1(0⁺) < exp2(0⁺).

Билет№11

1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при комплексно-сопряженных корнях характеристического уравнения.

(смотри Билет10, вопрос1, часть1)

Колебательный заряд конденсатора

В случае, если корни характеристического уравнения p_1,2 комплексные сопряженные, переходный процесс имеет колебательный характер. В данном случае и подкоренное выражение отрицательное. Корни характеристического уравнения в общем случае записываются в виде

,

где  – коэффициент затухания;

–частота свободных (собственных) колебаний контура.

Между исуществует следующая связь

.

Поскольку все изложенные выше выкладки применимы и для данного случая, запишем полное решение

.

Подставив в данную формулу выражения для и, получим:

.

Определим ток в контуре

Таким образом,

.

Введем и упростим выражение, полученное для:

,

тогда, обозначив , где,

Таким образом,

.

При построении графиков следует принимать во внимание соотношение между постоянной времени экспоненты и периодом синусоидыв свободной составляющей. Рассмотрим два варианта.

1.. В данном случае возможно графическое перемножение экспонентыи синусоиды(рис. 4.18).

2. . В данном случае возможно только аналитическое определение свободной составляющей (рис. 4.19). Для этого необходимо оценить время переходного процесса, где. Далее в зависимости от необходимой точности построения графика этот промежуток времени следует разбить наn интервалов t и далее рассчитать значение искомой функции в каждый момент .

Получим общий вид системы уравнений для определения постоянных интегрирования для случая комплексных корней характеристического уравнения. Как уже было показано, полное решение запишется

.

Для определения В₁ и В₂ составим систему уравнений:

Запишем дляt = 0⁺

Таким образом, искомая система уравнений имеет вид: