2. Линейные цепи переменного тока в установившемся режиме.

Задача 2. Руководствуясь графиками синусоидально изменяющихся токов i₁ … i₅, приведенными на рисунке 2.1, определите для каждого из токов его частоту, угловую частоту, амплитуду, действующее значение, мгновенное значение при t = 0,01 с, а также начальную фазу.

Рисунок 2.1

Представьте токи, в виде

• тригонометрических функций,

• комплексной алгебраической форме записи,

• комплексной показательной форме записи.

Найдите комплексные амплитуды токов. Изобразите токи векторами комплексных действующих значений.

1. Определяем частоты токов f - частота, это количество полных колебаний в секунду или f = (2.1)

T₁ = 0,02c = f₁ = == 50 Гц (2.2)

T₂ = 0,02c = f₂ = ==50 Гц (2.3)

T₃ = 0,02c= f₃ = ==50 Гц (2.4)

T₄ = 2, определяем время одного периода, из рисунка 2.1 находим цену одного деления 1/600 сек. Период повторения синусоидального изменяющегося тока i₄ Равен 16. следовательно можно найти f₄:

f₄ = 600/16 = 37,5 Гц или (2.5)

T₅ = 0,02с = f₅ =1/T₅ = = 50 Гц (2.6)

2. Определяем угловую частоту

Угловой (циклической) частотой синусоидально изменяющейся величины тока i, называется величина ω, показывающая скорость изменения фазы во времени. Зависимость частоты тока и угловой частоты определяется из формулы f = (2.7)

ω = f∙2π (2.8)

3. Находим ω угловую частоту искомых токов

ω₁= f₁2=2=1с^-1 (2.9)

ω₂= f₂2=2=1с^-1 (2.10)

ω₃= f₃2=2=1с^-1 (2.11)

ω₄= f₄2=2==0,75с^-1 (2.12)

ω₅= f₅2=2=1с^-1 (2.13)

4. Амплитуду искомых токов определяем по графику рисунок 2.1

Im₁ = 6 A

Im₂ = 4 A

Im₃ = 4 A

Im₄ = 7 A

Im₅ = 5 A

5. Определяем действующие значения токов:

I= (2.14)

I₁= = =4,24 (2.15) I₂= = =2,82 (2.16)

I₃= = =2,82 (2.17)

I₄= ==4,94 (2.18)

I₅= 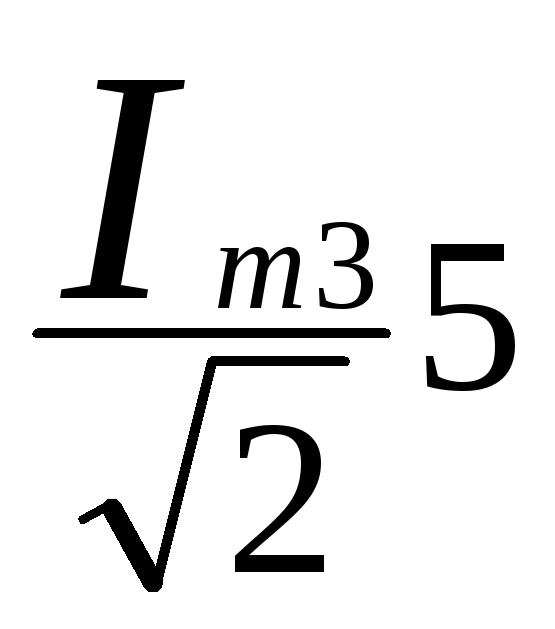==3,53 (2.19)

6. Определяем начальную фазу для каждого тока по графику на рисунке 2.1

₁= = 60⁰

₂= 0= 0⁰

₃= -= 300⁰

₄= -= 330⁰

₅= = 150⁰

7. Мгновенные значения токов при t=0,01 с можно определить графически используя рисунок 2.1 или аналитически зная формульную зависимость:

i=Imsin(ωt + ₁) (2.20)

где заданное время t = 0,01c соответствует углу 

i=Imsin(ω₁t + ₁) = 6 sin(1 + ) (2.21)

Из тригонометрии известно, что:

sin ( + ) = - sin, уравнение (2.21) примет вид:

i₁= 6 sin(1 + ) = -6sin=- =-5,196 A (2.22)

i₂=Im₂sin(ω₂t + ₂) = 4sin(+0) = 0 A (2.23)

i₃= Im₃sin(ω₃t + ₃) = 4sin(-) = 4 =3,46 A (2.24)

i₄= Im₄sin(ω₄t + ₄) = 7sin(-) = 7sin() =7sin(-) =

= 7sin()= 7sin75⁰=6,77A (2.25)

I₅= Im₅sin(ω₅t + ₅) = 5sin(-) = 5sin() =5 = 2,5 A (2.26)

8. Определены все величины синусоидальных изменяющихся токов для представления их в виде тригонометрических функций:

i₁= 6 sin(t + ) (2.27)

i₂= 4 sint (2.28)

i₃= 4 sin(t - ) (2.29)

i₄= 7 sin(t + ) (2.30)

i₅= 5 sin(t - ) (2.31)

2.1 Представление искомых токов в комплексной показательной форме записи.

Соответствие между величинами, изменяющимися синусоидально и комплексными числами установлены следующим образом:

• модуль комплексного числа принимается равным действующему значению;

• аргумент комплексного числа равен начальной фазе синусоиды.

i=Imsin(ωt + _i) I_i= I_ie^j (2.32)

İ₁=I₁ e^j1 = 4,24 e ^j (2.33)

İ ₂=I₂ e^j2 = 2,82 e ^{j0 =} 2,82 (2,34)

İ ₃=I₃ e^j3 = 2,82 e ^{- j} (2,35)

İ ₄=I₄ e^j4 = 4,94 e ^{- j} (2,36)

İ ₅=I₅e^j5 = 3,53e^{- j}(2,37)

2.2 Представление искомых токов в комплексной алгебраической форме записи.

Для решения данной задачи, используем формульную зависимость перехода от показательной формы записи к алгебраической.

Ż = Ze^j = Zcos + jZsin (2.38)

Нам также потребуются формулы приведения:

sin (180 - ) = sin (2.39)

cos(180 -) = -cos(2.40)

sin( -) = -sin(2.41)

cos( -) =cos(2.42)

İ ₁= 4,24 e ^j = 4,24 cos+ j4,24sin = 4,24cos60+ j4,24sin 60 =

= 2,12 + j3,67 (2.43)

İ ₂= 2,82 e ^j0 = 2,82 cos0+ j2,82sin0 = 2,82 (2.44)

İ ₃= 2,82 e ^{- j} = 2,82 cos^(-)+ j2,82sin^(-) = -1,41 - j2,44 (2.45)

İ ₄= 4,94 e ^{- j} = 4,94 cos^(-)+ j4,94sin^(-) = 4,27 - j2,47 (2.46)

İ ₅= 3,53 e ^{- j} = 3,53 cos^(-)+ j3,53sin^(-) = -3,06 – j1,77 (2.47)

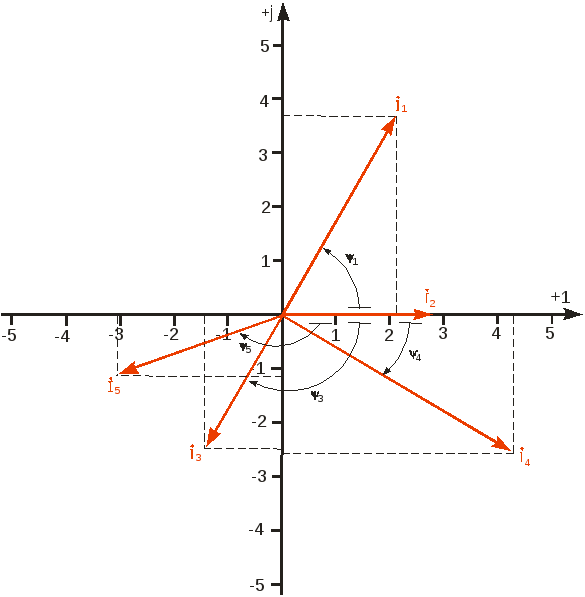
Рисунок 2.2

Задача 3

Определите токи в ветвях и напряжения на элементах цепи переменного тока частотой 50 Гц, схема которой изображена на рисунке 3.1

Расчет выполните всеми перечисленными ниже методами:

1) метод непосредственного применения законов Кирхгофа ,

2) метод наложения,

3) метод эквивалентного генератора (определите ток в одной из ветвей цепи).

Составьте баланс активной и реактивной мощностей. Определите показания амперметра. Постройте векторную диаграмму токов и напряжений. Исходные данные для решения задачи указаны в таблице 3.1

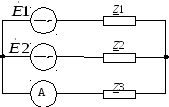
Рисунок 3.1

Таблица 3.1

Ė1 В	Ė2 В	Z 1 ОМ	Z 2 ОМ	Z 3 ОМ
48e-jπ/6	24e-jπ/3	10 – j10	6 – j8	4 - j3