МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра теоретических основ электротехники

Расчётно-графическая работа № 2

По дисциплине «Электротехника».

" Расчет электрических цепей однофазного синусоидального тока".

Выполнил: студент группы

ИСТ-212

Каримова Д.Р.

Принял:

доцент Крайнова Т.М.

УФА 2009

Задание:

R₁ =0 Ом R₂ = 24 Ом R₃ = 0 Ом

L₁ = 99 мГн L₂ = 13 мГн L₃ = 61 мГн

C₁ = 0 мкФ C₂ = 84 мкФ C₃ = 60 мкФ

E₁ = 0 B E₂ = 168 В E₃ = 42 В

φ₁ = 0 φ₂ = 273 φ₃ = 207

f = 50 Гц

 = 314 Гц

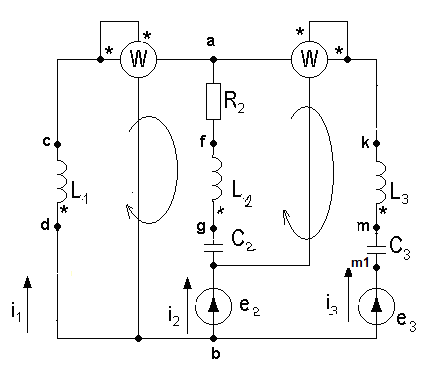
Расчетная схема цепи.

1. Найдем комплексы действующих значений токов во всех ветвях.

Найдем комплексные сопротивления каждой ветви.

Z₁ = j X _L1 = j 31,086 Ом

Х_L1 = L₁ =314*99*10^-3 =31,086 Ом

Z₂ = R₂ + j(Х_L2 – X_C2) =24 – j 33,831 Ом

Х_L2 = wL₂ =314*13*10^-3 =4,082 Ом

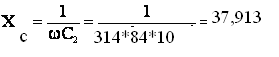
Z₃ = j(Х_L3 – X_C3) = - j 33,924 Ом

Х_L3 = L₃ = 314 * 61*10^-3 = 19,154 Ом

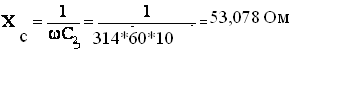
Найдем комплексные ЭДС.

Ė₁ = 0 B

Ė₂ = 168 e^j273 = E₂* cosφ₂ + j E₂ * sinφ₂ = 168 * cos273˚ + j 168 * sin273˚ =

= 8,792 - j 167,769 B

Ė_{3 =} 42 e^j207 = E₃ * cosφ₃ + j E₃ * sinφ₃ = 42 * cos207˚ + j 42 * sin207˚ =

= -37,422- j 19,067 B

Метод контурных токов.

İ₁ = İ₁₁

İ₂ = İ₂₂ – İ₁₁

İ₃ = – İ₂₂

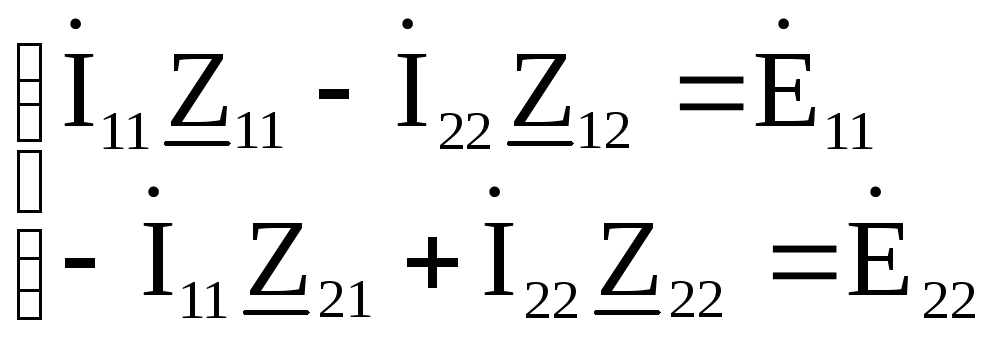
Найдем комплексные значения собственных и смежных сопротивлений.

Z₁₁ = Z₁ + Z₂ = 24 – j 2,745Ом

Z₂₂ = Z₂ + Z₃ = 24 – j 67,755 Ом

Z₁₂ = Z₂₁ = Z₂ = 24 – j 33,831 Ом

Найдем комплексные значения собственных ЭДС контуров.

Ė₁₁ = – Ė₂= -8,792 + j 167,769 B

Ė₂₂ = Ė₂ – Ė₃ = 46,214 – j148,702 B

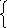
(24 – j 2,745) * İ₁₁ – (24 – j 33,831) * İ₂₂ = -8,792 + j 167,769

– (24 – j 33,831) * İ₁₁ + (24 – j 67,755) * İ₂₂ = 46,214 – j148,702

İ₁₁ = 7.54714+ j 0.00406 A

İ₂₂ =6.35371+ j 1.10684 A

Искомые комплексные токи.

İ₁ =7.54714+ j 0.00406 = 7.54714e^j180.03A

İ₂ = -1.19343+ j1.10278 = 1.62493 e^j137.3 A

İ₃ = -6.35371- j1.10684 = 6.44939e^j189 A

Найдем показания ваттметров

Для этого найдем напряжение U_an и U_ab.

U_an = – İ₂ Z_2.

U_an = (1.19343 - j1.10278)* (24 – j 33,831)=-8.66583-66.84165 j=67.40105 e^j262.6

U_ab. =– İ₁ Z₁ =(-7.54714-j 0.00406 )* j 31,086=-234.61039 j+0.1262=

234.61042 e^j270.1

P_W1 = Re [U_ab * I₁^*]

P_W1 = Re [234.61042 e^j270.1 *7.54714e^-j180.03 ]=[1770 e^j90]=0 Вт

P_W2 = Re [U_an * I₃^*]== Re[67.40105 e^j262.6 *6.44939e-^j189 ]=Re[434.69565* e^j73.6 ]=Re[122.7326031+417.00961 j ]=122.73260Вт

Уравнения Кирхгофа в дифференциальных и комплексных формах при магнитной связи между двумя индуктивностями.

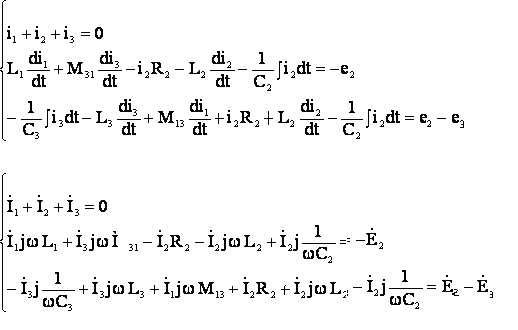
S_ист = Ė₂İ₂ + Ė₃İ₃ =168 e^j273 *7.54714e^j180.03 + 42 e^j207 *6.44939e^j189=152.12+1425.36 j

P_ист = Re [S_ист]= 152.12 Вт

Q_ист = Im [S_ист] =1425.36 ВАР

S_пр = İ₁²Z₁ + İ₂² Z₂ + İ₃² Z_{3 =}7.54714. ² (j 31,086)+ 1.62493 ² (24 – j 33,831) +

+ 6.44939²(–j 33,924)= 153.11++1423j

P_пр = Re [S_пр] =153.11 Вт

Q_пр = Im [S_пр]=1425.22 ВАР

Т.к. P_пр = P_ист и Q_пр = Q_ист , то баланс активных и реактивных мощностей сходится.

4. Топографическая диаграмма напряжений и векторная диаграмма токов