
примеры решений задач / Расчётка2
.docУфимский государственный авиационный технический университет
Кафедра теоретических основ электротехники
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №2
Расчёт переходных процессов в линейных цепях
Выполнил: Кузьмина А. О.
Группа: ЗИ-229
Проверил: Чечулина Ирина
Евгеньевна
Уфа 2008
Задача 1.В соответствии с индивидуальным заданием дана электрическая цепь, в которой в момент времени t происходит коммутация. В цепи действует постоянное ЭДС E.
Требуется определить закон изменения во времени тока после коммутаций в одной из указанных ветвей схемы или напряжение, на каком либо элементе.
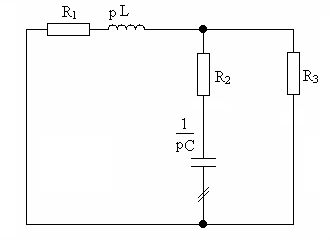
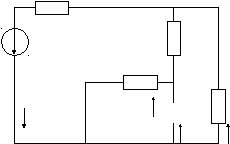
Схема №2
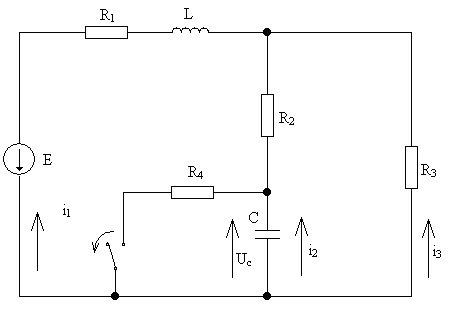
Задания:
1.Рассчитать закон изменения тока (напряжения) в функции времени классическим методом.
2.Рассчитать закон изменения тока (напряжения) в функции времени операторным методом.
3. На основании полученного аналитического выражения построить график
Изменение искомой величины
в зависимости от времени на интервале
от t
=0 до t=3![]() .
.
1.Расчет закона изменения тока i2(t) в функции времени классическим методом.
1)Уравнения для послекоммутационной цепи :
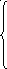
![]()
Цепь второго порядка , содержит два накопителя энергии , следовательно уравнение содержит два свободных состояния.
![]()
![]()
![]()
2)Расчёт установившегося режима и определение токов в этом режиме
![]()
![]()
![]()
3) Нахождение корней характеристического уравнения
Разомкнём цепь на конденсаторе

![]() ;
;
![]()
![]()
![]()
![]()
![]() c-1
c-1
![]() c-1
c-1
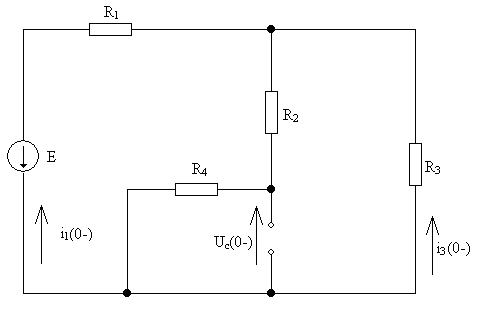
4)Определяем начальные независимые условия
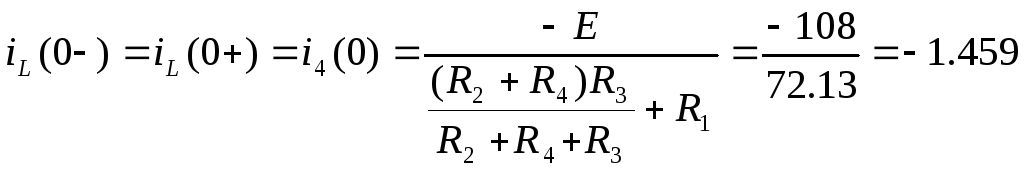 А
А
![]() A
A
![]() В
В
5)Определение зависимых условий.

По закону Кирхгофа:
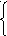
![]()
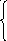
![]()
![]()
![]()
![]() А
А
![]() А
А
6)Вычисление постоянных интегрирования.
t = 0;
= 0;
![]()
![]()
![]()
![]()
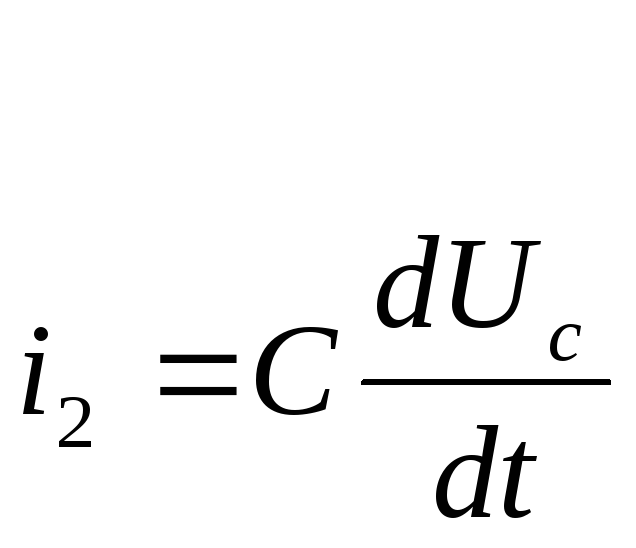
![]()
![]() В/с
В/с
![]()
![]()
![]() А/с
А/с
![]()
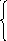
![]()
![]()
![]()
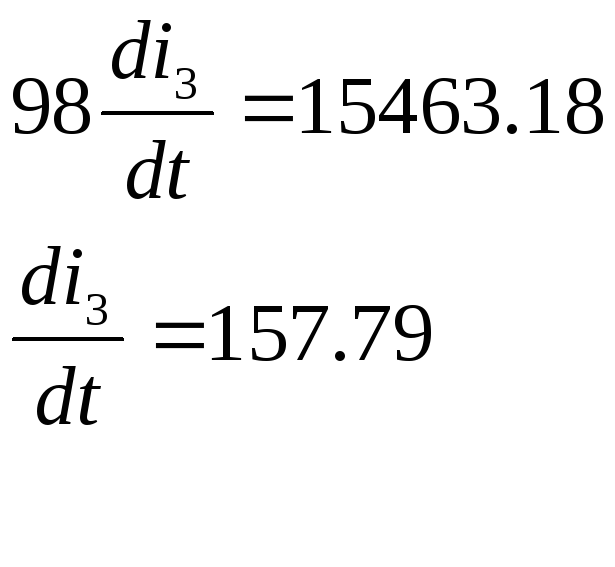
![]() А/с
А/с
При t =0
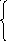
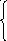
![]()
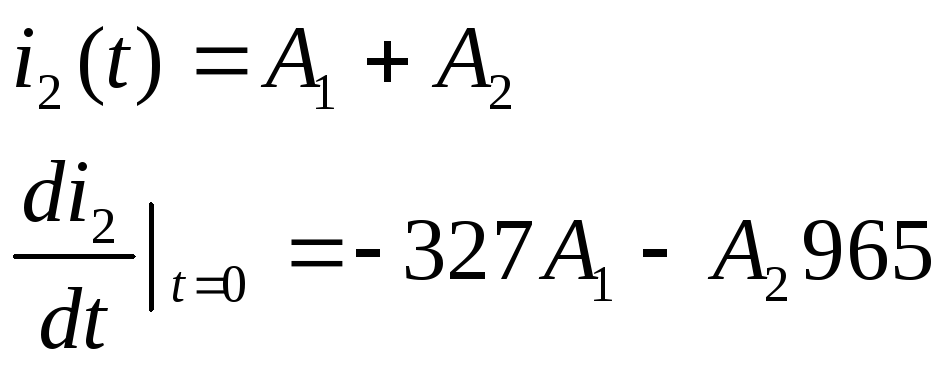 =>
=>![]()
![]()
A1=0.8138
A2=-0.4838
Ответ:
![]() А
А
2.Расчет закона изменения тока i2(t) в функции времени операторным методом.
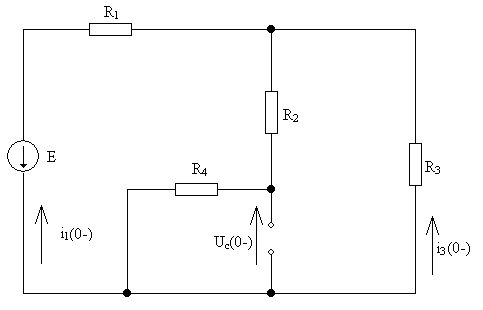
1)Определяем начальные независимые условия
![]() А
А
![]() В
В
2)Составляем операторную схему для послекоммутационной цепи.
Послекоммутационный режим ключ разомкнут.
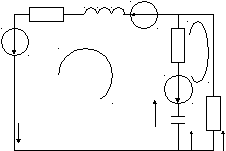
Уравнения по закону Кирхгофа в операторной форме:
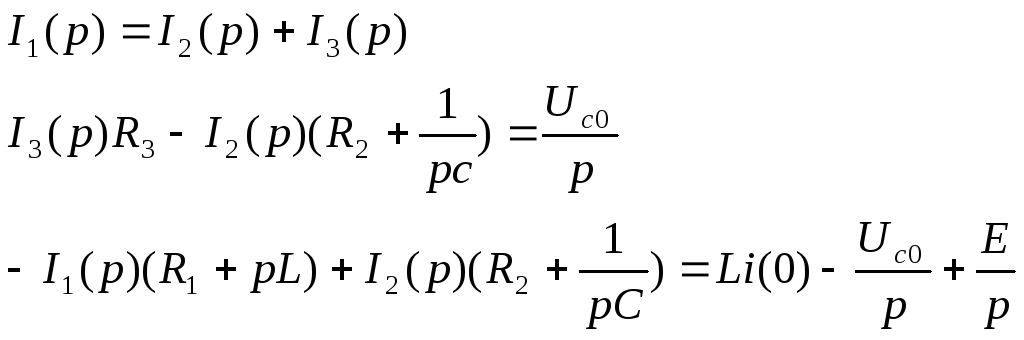
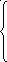
![]()
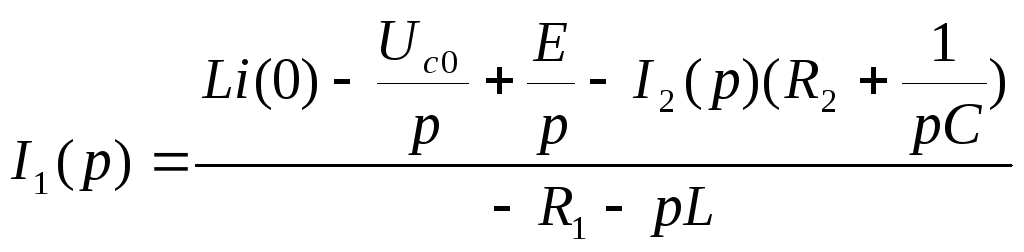
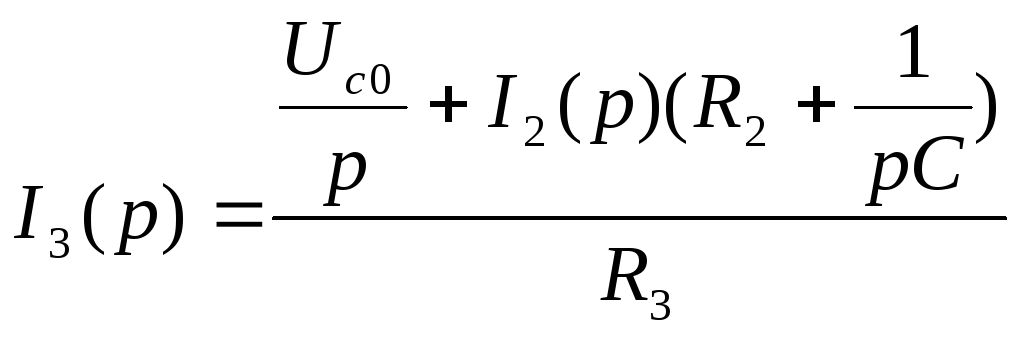
![]()
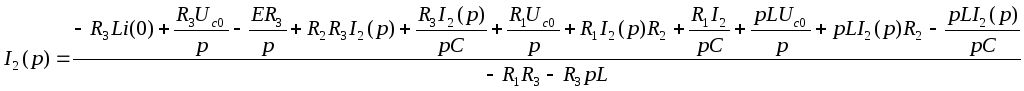
![]()
![]()
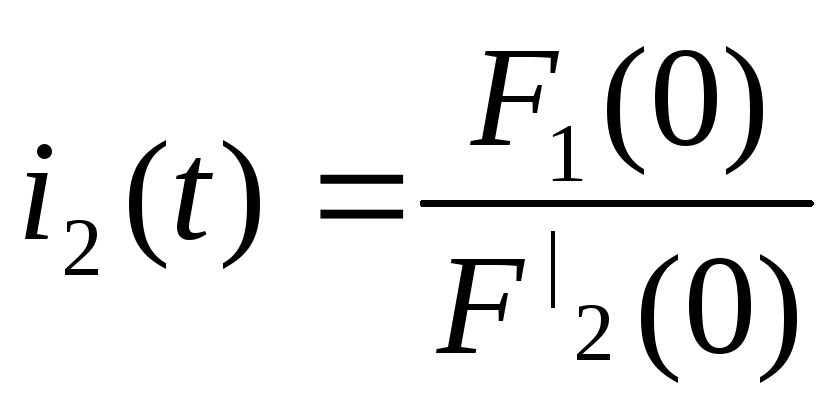
Находим корни характеристического уравнения:
![]()
![]() c-1
c-1
![]() c-1
c-1
Находим оригинал:
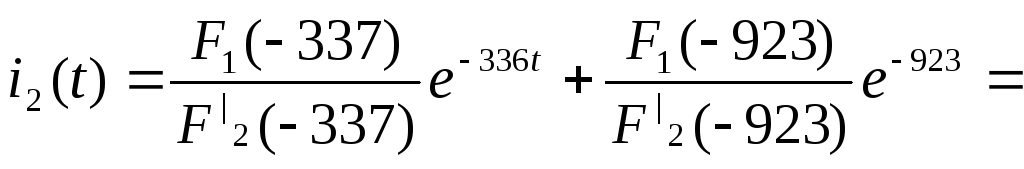
![]() А
А
Зависимость переходного тока от времени.
р1 = –327с-1 р2 = –965 с-1
График строим на интервале от t =0 до t = 3/|pmin| = 0,01 c.
![]()
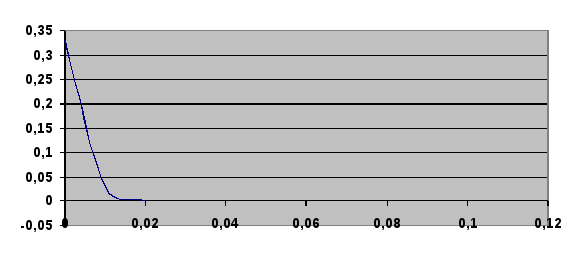
Вывод: в ходе данной расчетно-графической работы был рассчитан третий ток в данной схеме классическим и операторным методом.
Задача №2
Определить закон изменения во времени тока в указанной ветви схемы.

 Классический метод
Классический метод
1)

![]()
![]()
![]() А
А
2)Нахождение корней характеристического уравнения


![]()
![]() В
В
![]()
![]() с-1
с-1
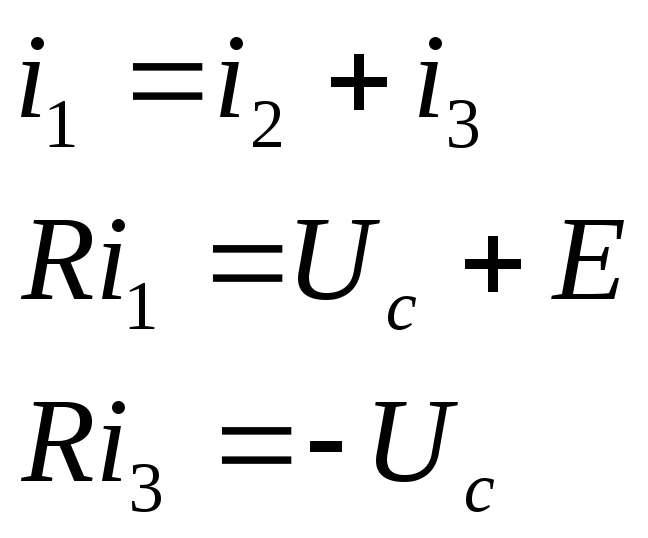 =>
=>
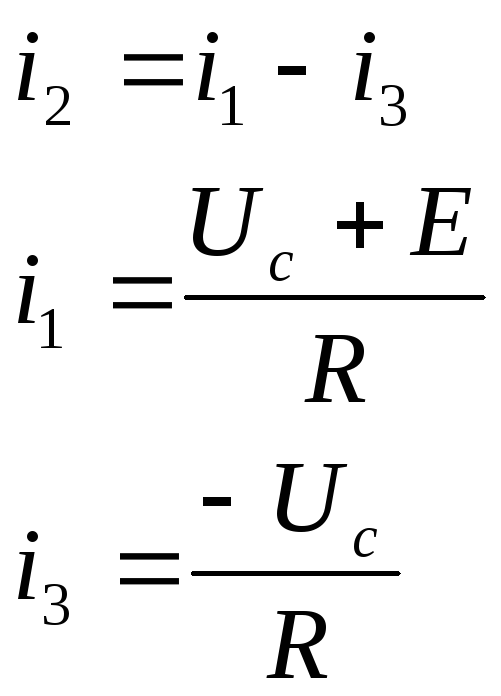
![]() А
А
![]() При E=1
При E=1
![]()
![]()
Рассмотрим момент времени
![]()
![]()
![]()
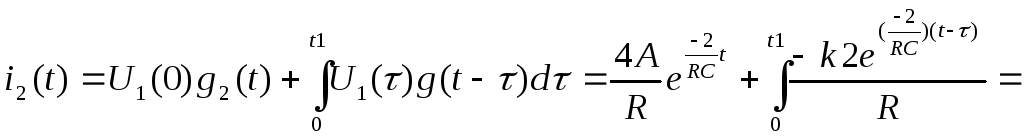
![]()
Момент времени
![]()
![]()
![]()
![]() +
+![]()
