
примеры решений задач / raschet_lineynyh_cepey_postoyannogo_i_peremennogo_toka
.docРасчетно-графическая работа №1
Дано:
![]()
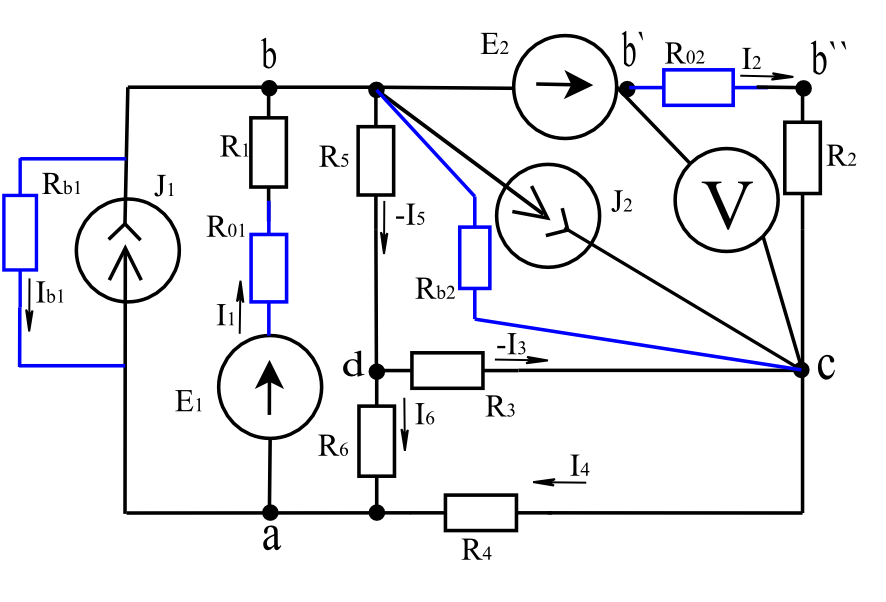
R2 = 12 Ом R02 = 0,1 Ом
R3 = 8 Ом Rв1 = 2 Ом
R4 = 12 Ом Rв2 = 1 Ом
R5 = 15 Ом Е1 = 70 В
R6 = 10 Ом Е2 = 90 Ом
J1 = 0,5 А J2 = 0,7 А
_______________________
Рис.1 Схема линейной электрической
цепи постоянного тока
Ход работы.
-
Составим на основании законов Кирхгофа систему уравнений для расчета токов в ветвях электрической цепи (математическая модель)
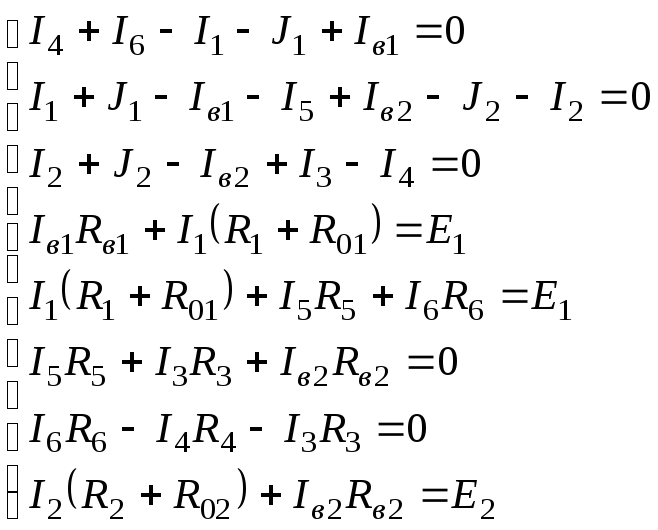
-
Определим токи во всех ветвях электрической цепи методом контурных токов
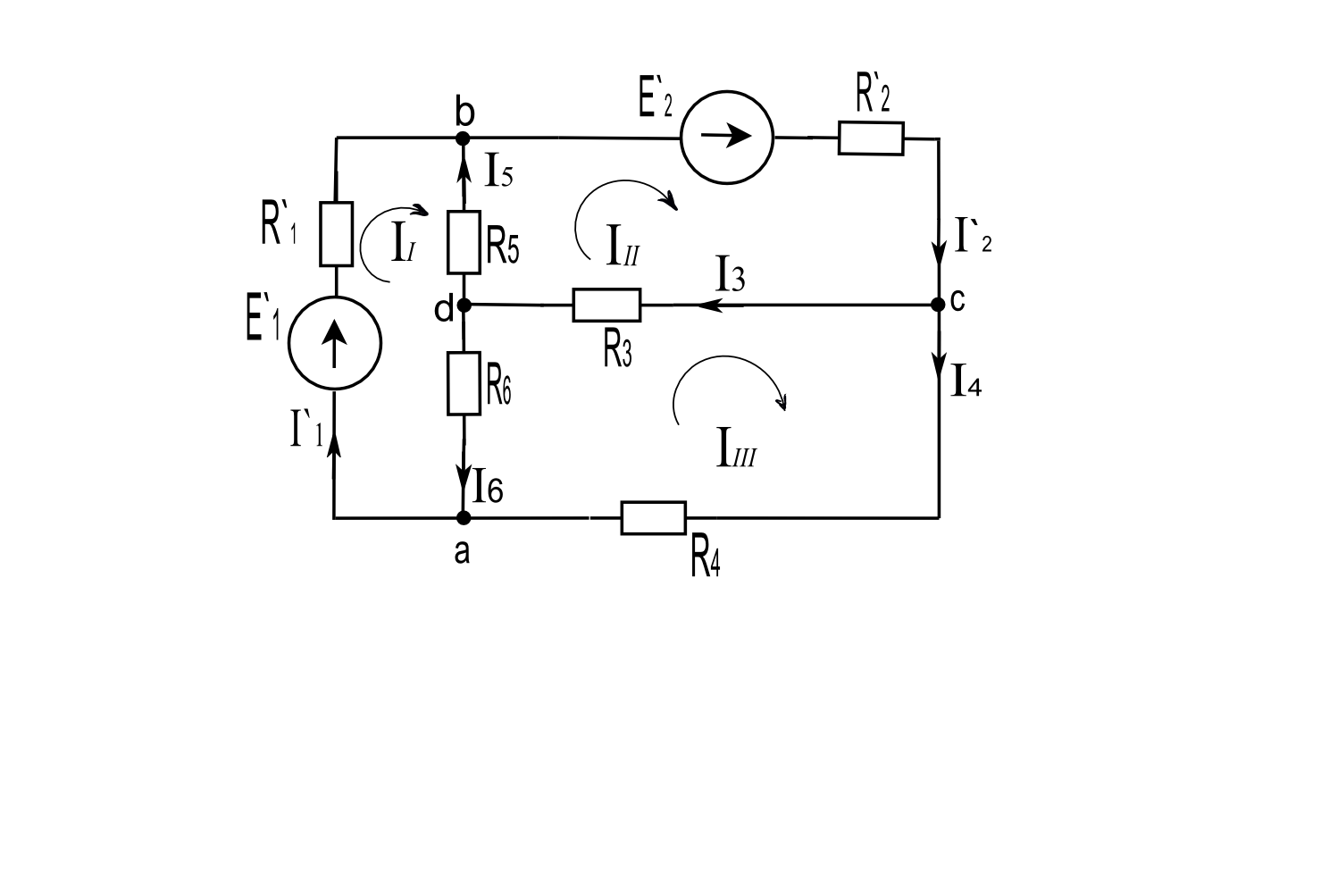
Рис.2 Преобразованная схема цепи (расчет контурных токов)
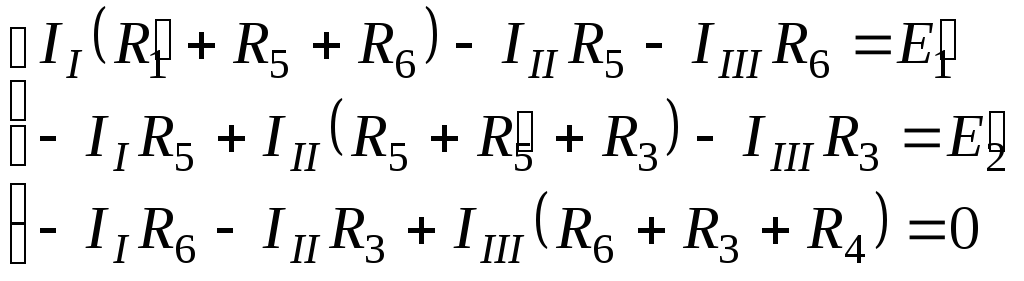
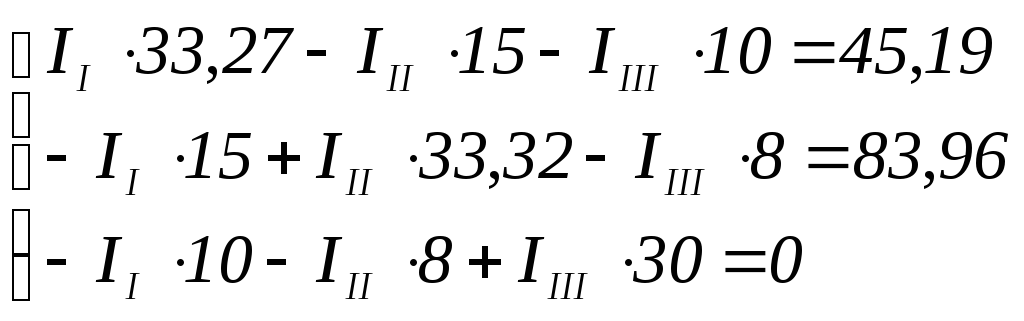
Решаем систему с помощью определителей
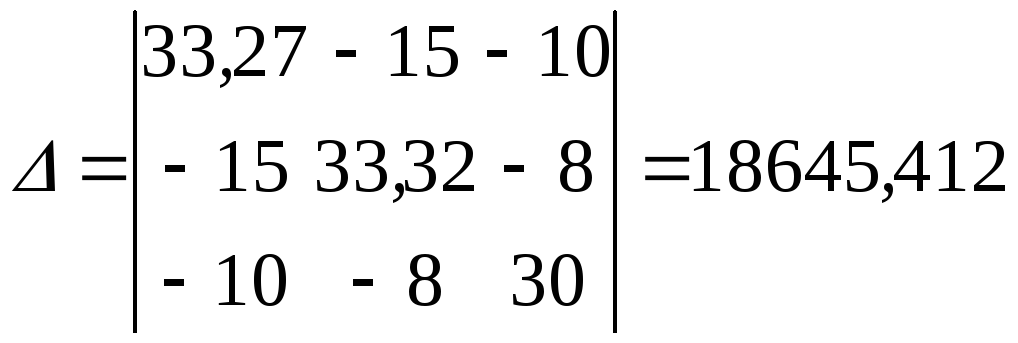 (Ом2)
(Ом2)
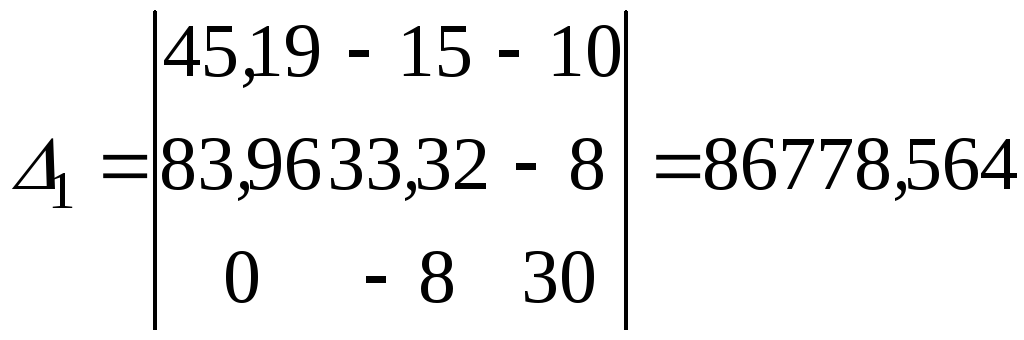 (ВОм2)
(ВОм2)
![]() А
А
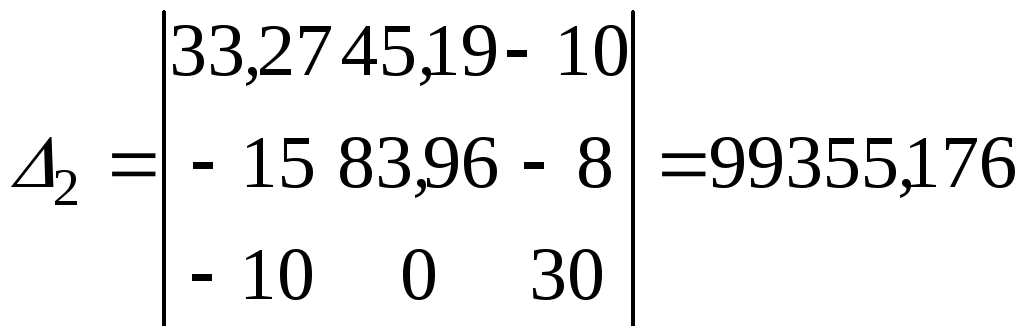 (ВОм2)
(ВОм2)
![]() А
А
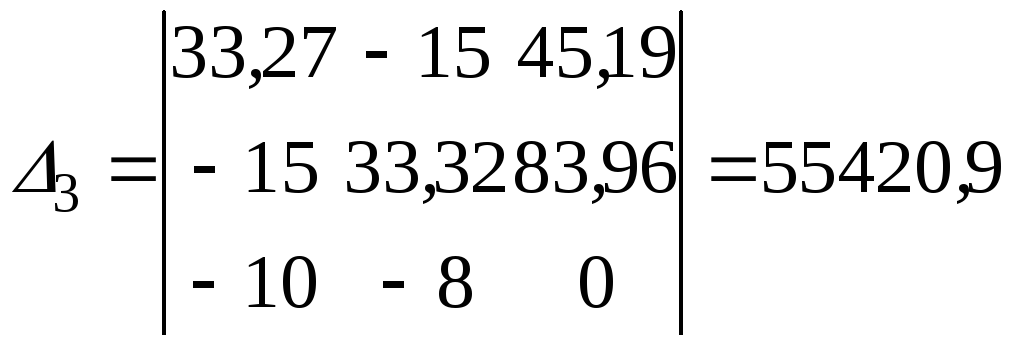 (ВОм2)
(ВОм2)
![]() А
А
Токи в ветвях:
![]() А
А ![]() А
А
![]() А
А ![]() А
А
![]() А
А ![]() А
А
![]() В
В
![]() В
В
![]() А
А ![]() А
А
![]() В
В
![]() А
А ![]() А
А
-
Определим токи во всех ветвях электрической сети методом узловых потенциалов
![]() - заземлен;
- заземлен;
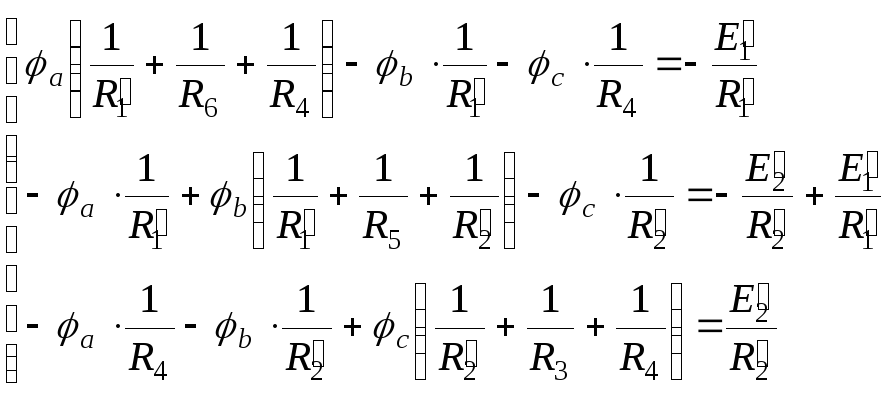
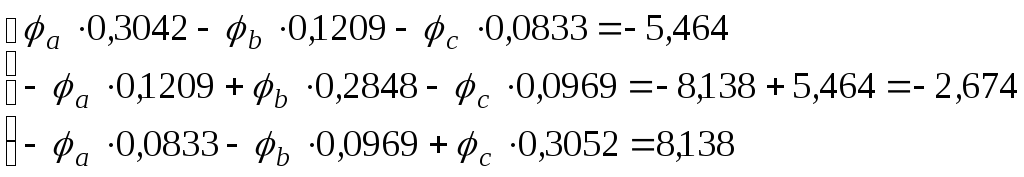
Решаем систему уравнений с помощью определителей
 (См2)
(См2)
 (АСм2)
(АСм2)
![]() В
В
 (АСм2)
(АСм2)
![]() В
В
 (АСм2)
(АСм2)
![]() В
В
Токи в ветвях:
![]() А
А
![]() А
А
![]() А
А
![]() А
А
![]() А
А
![]() А
А
![]() А
А
![]() А
А
-
Предварительно упростив схему, заменив треугольник сопротивлений, составленных из пассивных элементов, эквивалентной трехлучевой звездой, определим токи во всех ветвях исходной электрической цепи, применив метод узловых напряжений (метод двух узлов)
Упрощаем схему:
![]() A
A ![]() A
A
![]() A
A ![]() A
A
![]() Ом
Ом ![]() Ом
Ом
![]() В
В ![]() В
В
Определим токи методом двух узлов. Заменим треугольник сопротивле ний, эквивалентной трехлучевой звездой
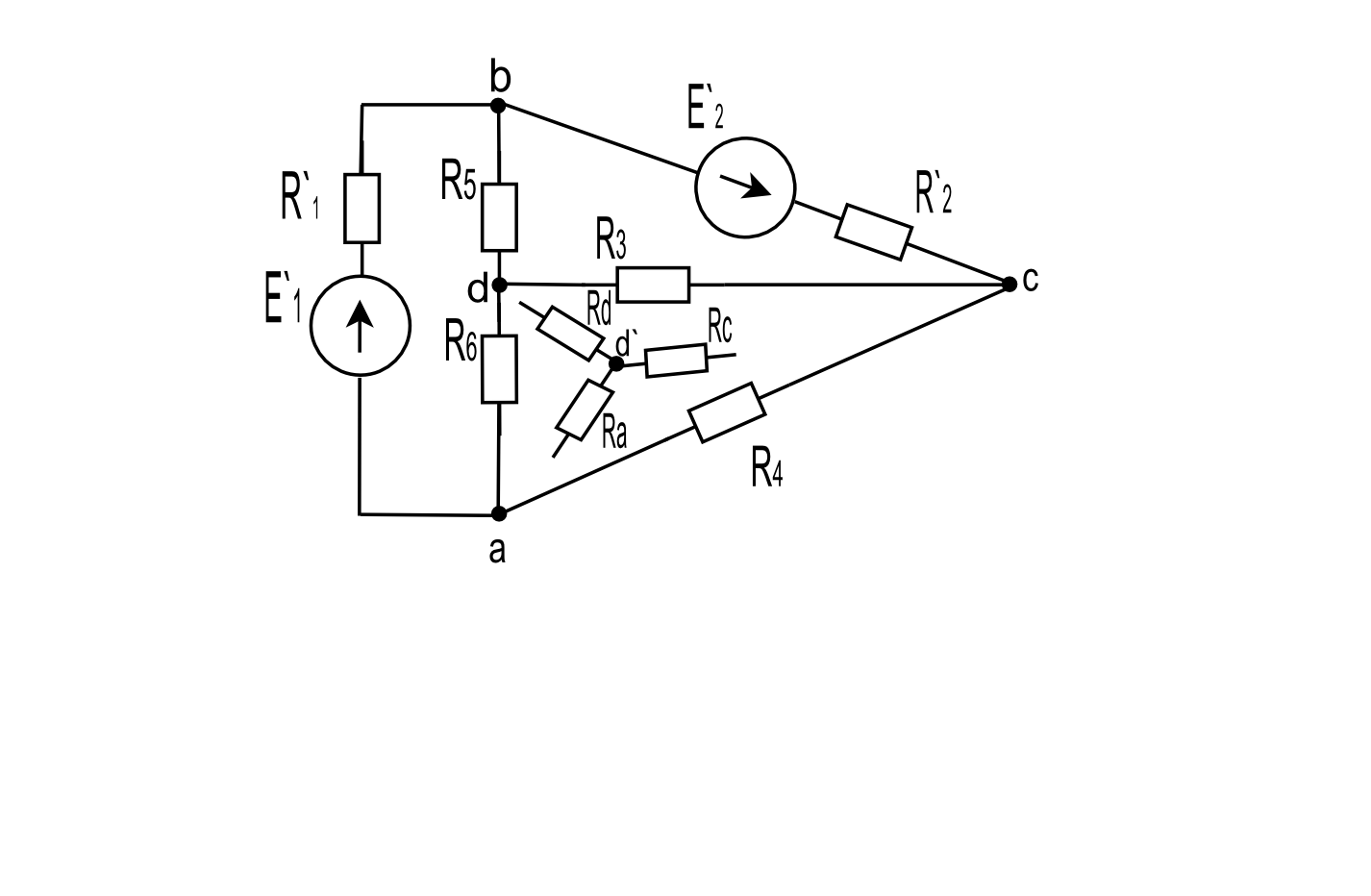
Рис.3 Треугольник сопротивлений (эквивалентной трехлучевой звездой)
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
Проводимость ветвей:
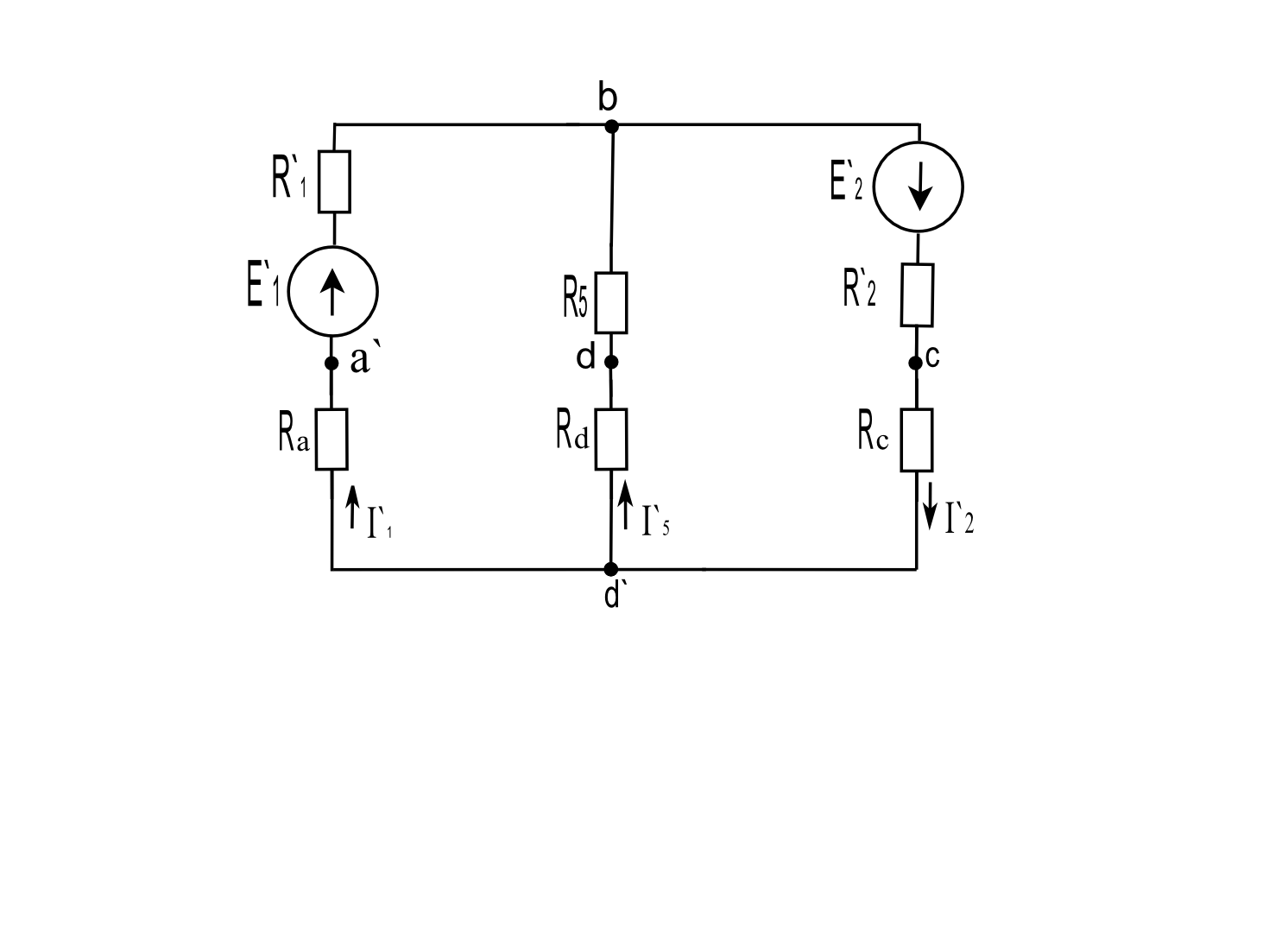
Рис.4 Схема ветвей
![]() См
См
![]() См
См
![]() См
См
![]() См
См
![]() В
В
![]() В
В
![]() А
А
![]() А
А
![]() А
А
![]() В
В
![]() А
А
![]() В
В
![]() A
A
![]() В
В
![]()
![]() В
В
![]() В
В
![]() А
А ![]() А
А
![]() В
В
![]() А
А ![]() А
А
-
О
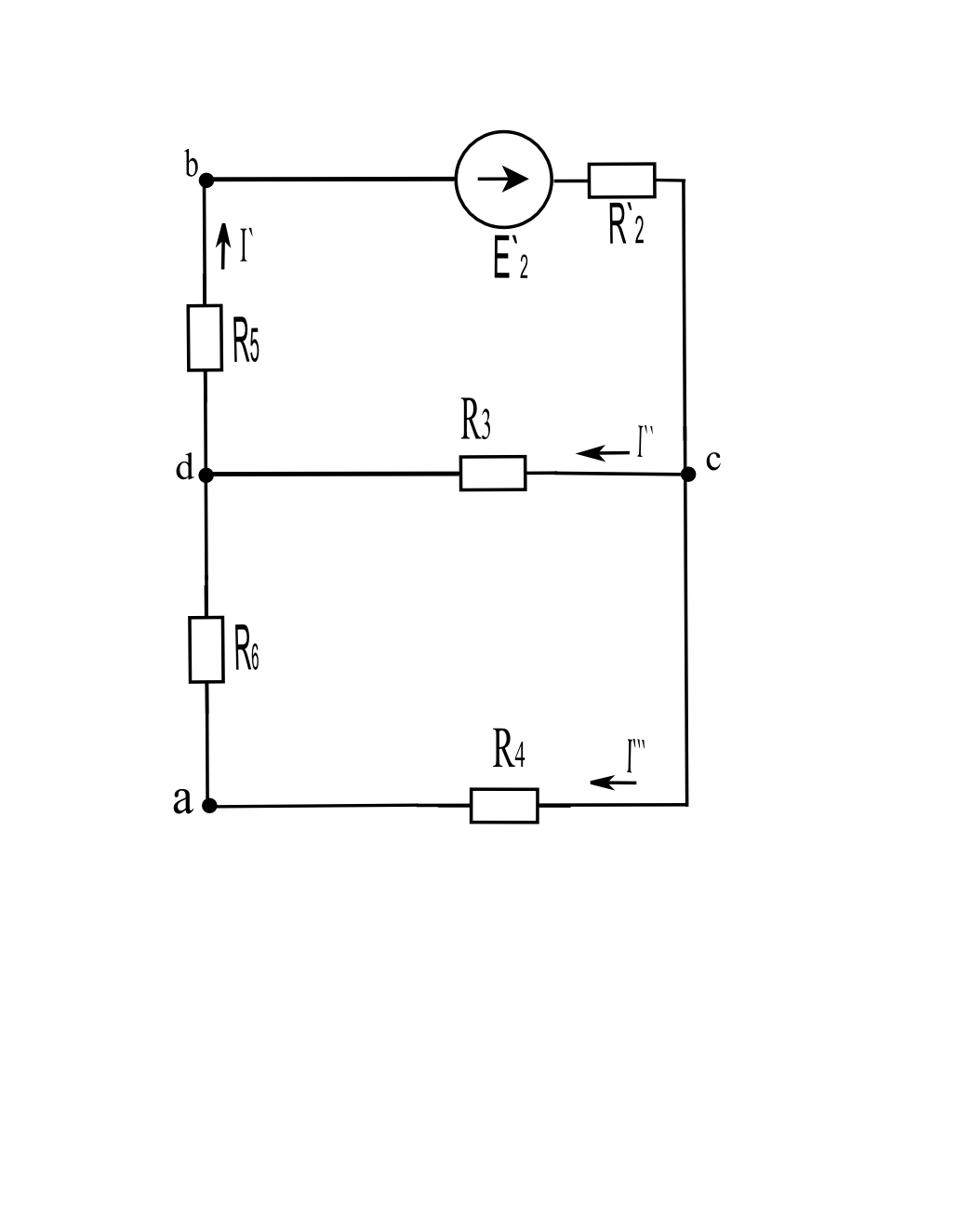 пределить
ток в ветви с резистором R1
методом эквивалентного генератора.(Ветвь
с
пределить
ток в ветви с резистором R1
методом эквивалентного генератора.(Ветвь
с
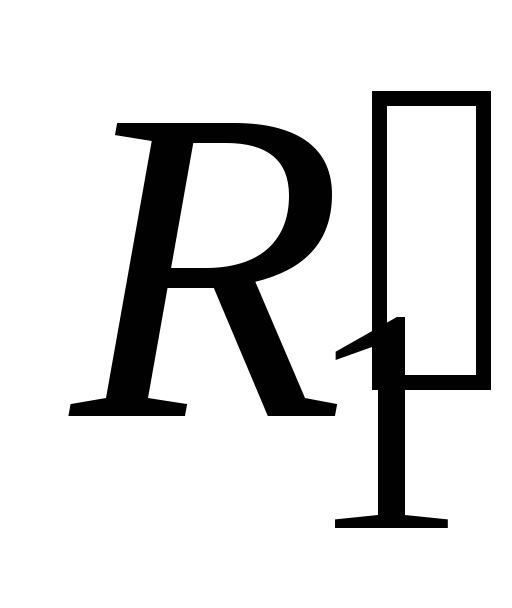 отключаем)
отключаем)
Рис.5 Определение токов в ветвях
Определим токи в новой схеме
![]() Ом
Ом
![]() А
А
![]() В
В
![]() А
А
![]() А
А
ЭДС эквивалентного генератора
![]()
 В
В
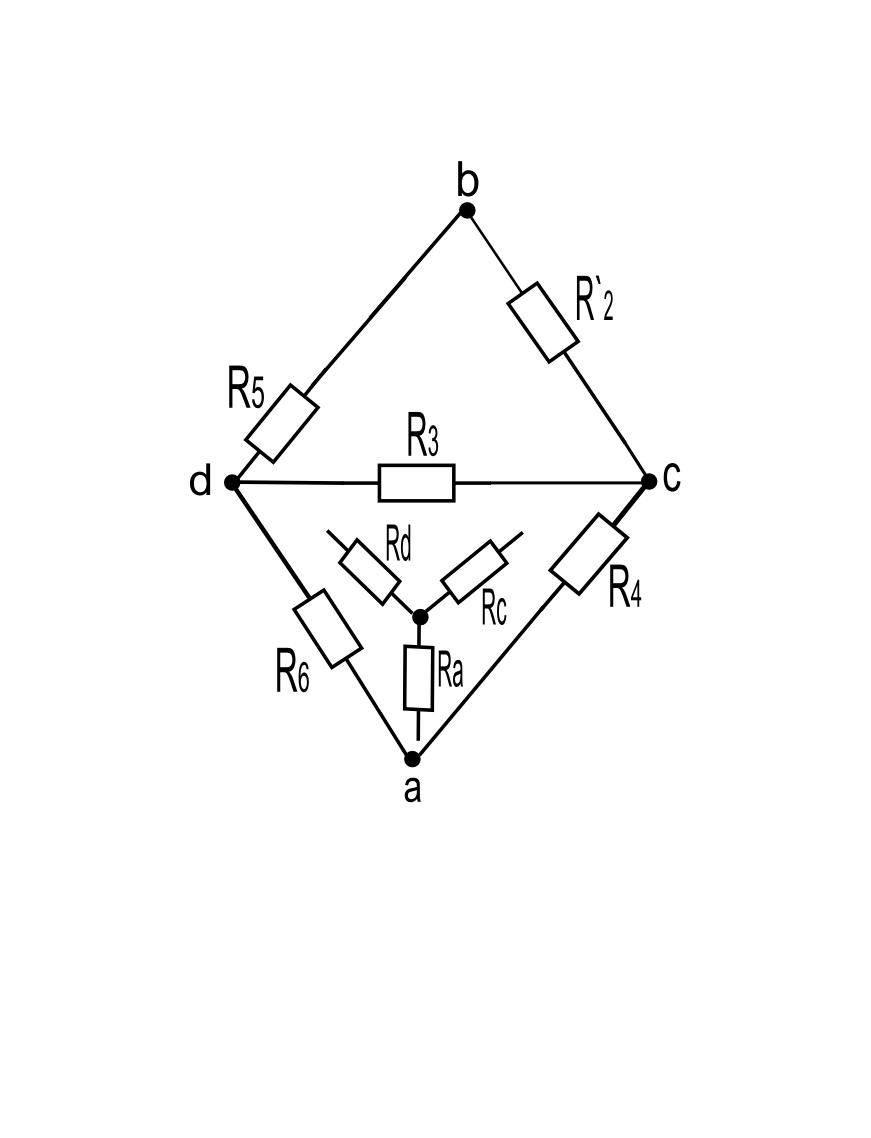
Определим внутреннее сопротивление эквивалентного генератора.
Заменим треугольник на звезду.
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом

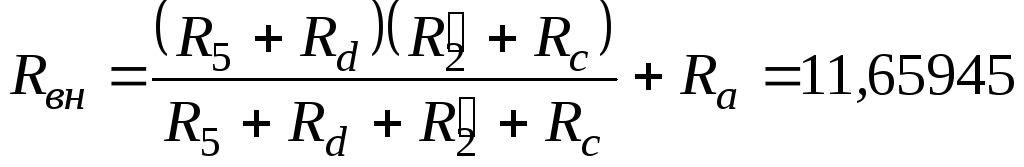 Ом
Ом
Рис.6 Замена треугольник на звезду
![]() А
А
![]() В
В
![]() В
В
![]() А
А
-
Результаты расчетов токов указанными в п.п. 2, 3, 4 и 5 методами сводим в таблицу и сравним их.
|
Ток Метод |
|
|
|
|
|
|
|
|
|
|
|
Метод контурных токов |
4,654 |
4,491 |
5,33 |
5,041 |
2,358 |
2,972 |
0,676 |
1,682 |
0,334 |
0,414 |
|
Метод узловых потенциалов |
|
4,4886 |
|
5,047 |
2,353 |
2,97 |
0,6735 |
1,6816 |
0,3355 |
0,41325 |
|
Метод 2-х узлов |
4,655 |
4,4902 |
5,33 |
5,042 |
2,3574 |
2,973 |
0,6753 |
1,6817 |
0,3344 |
0,41412 |
|
Метод эквивалентного генератора |
4,6539 |
4,4892 |
|
|
|
|
|
|
|
|
-
Определим показания вольтметра.
![]() В
В
-
Составляем баланс мощностей для исходной электрической цепи.
![]()
Мощность источников:
![]() Вт
Вт
Мощность приемников:
![]()
![]() Вт
Вт
Баланс мощностей выполняется:
![]() Вт
Вт
Погрешность:
![]()
-
Строим в масштабе потенциальную диаграмму для внешнего контура.
Для построения потенциально диаграммы
по внешнему контуру определим потенциалы
точек внешнего контура (![]() заземлен) на Рис.1.
заземлен) на Рис.1.
![]() В
В
![]() В
В
![]() В
В
![]() В
В
![]() В
В
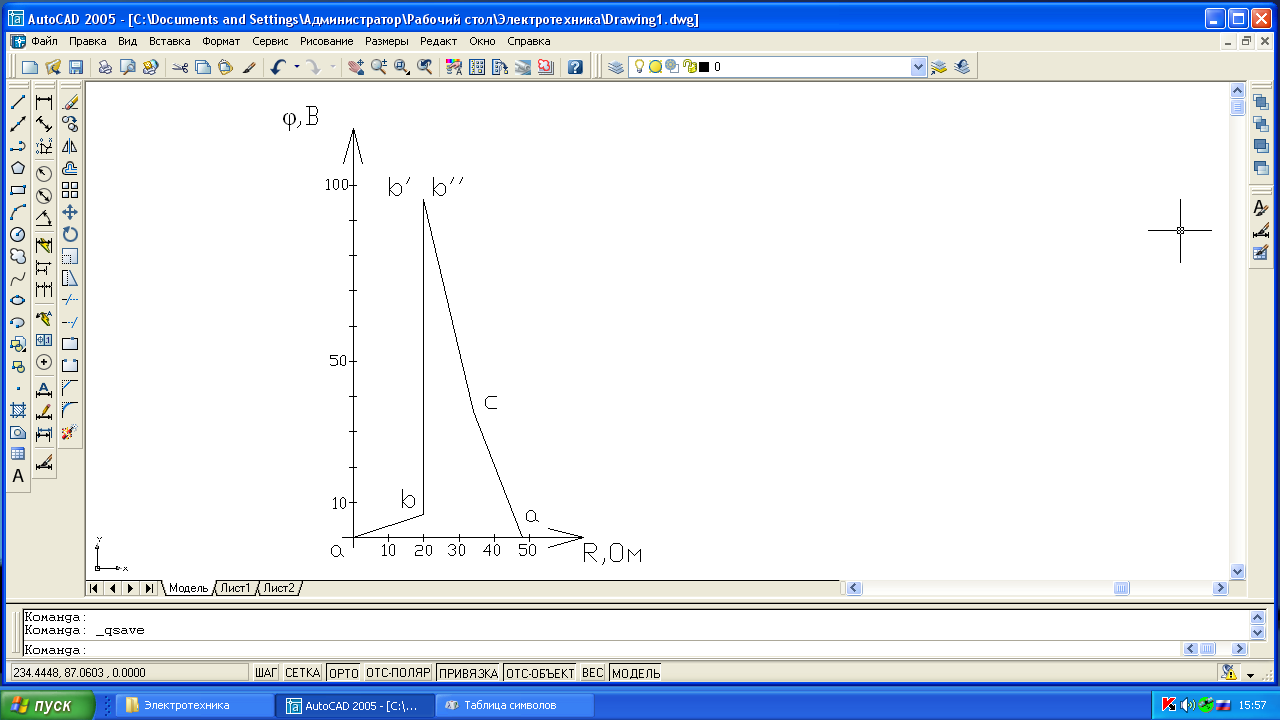
Рис.8 Потенциальная диаграмма внешнего контура
Расчетно-графическая работа №2
Дано:
Uл = 380 В
f = 50 Гц
RA = 10 Ом
RB = 4 Ом
RC = 100 Ом
LC = 15,9 мГн
СA = 318 мкФ
СB = 637 мкФ
_____________________
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
PA,
PB,
PC,
Pn
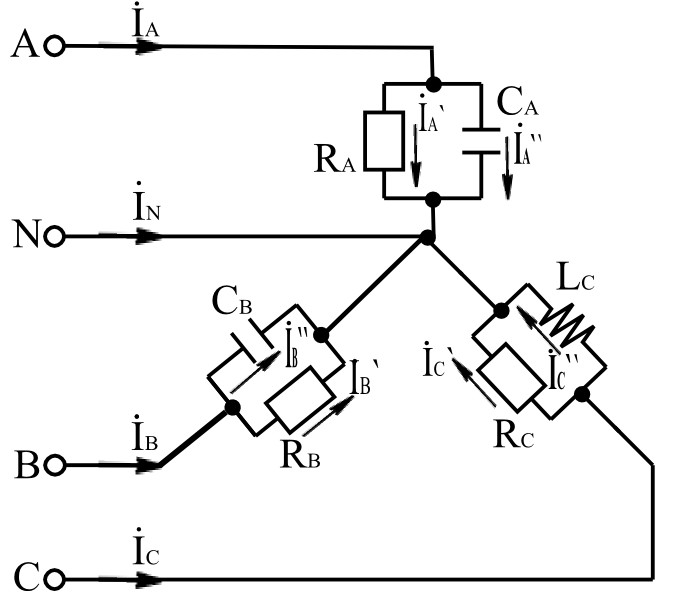
- ? Рис.1
Трехфазная электрическая цепь
синусоидального тока
,
PA,
PB,
PC,
Pn
- ? Рис.1
Трехфазная электрическая цепь
синусоидального тока
Ход работы.
Для трехфазной электрической цепи синусоидального тока определим следующее:
-
Вычислим фазные и линейные токи
(решение производим с помощью комплексных чисел)
Угловая частота:
![]() рад/с.
рад/с.
Реактивные сопротивления фаз:
![]() Ом
Ом
![]() Ом
Ом
![]() Ом
Ом
Считаем, что вектор фазного напряжения
![]() направлен по действительной оси, тогда
направлен по действительной оси, тогда
![]() В,
В,
![]() В,
В,
![]() В.
В.
Находим линейные и фазные токи:
![]() А
А
![]() А
А
![]() А
А
![]() А
А
![]() А
А
![]() А
А
![]() А
А
![]() А
А
![]() А
А
-
Для четырехпроводной цепи определим ток в нейтральном проводе
![]() А
А
-
Определим активную мощность во всей цепи и в каждой фазе отдельно
Определяем активную мощность фаз и всей цепи:
![]() Вт
Вт
![]() Вт
Вт
![]() Вт
Вт
![]() Вт
Вт
-
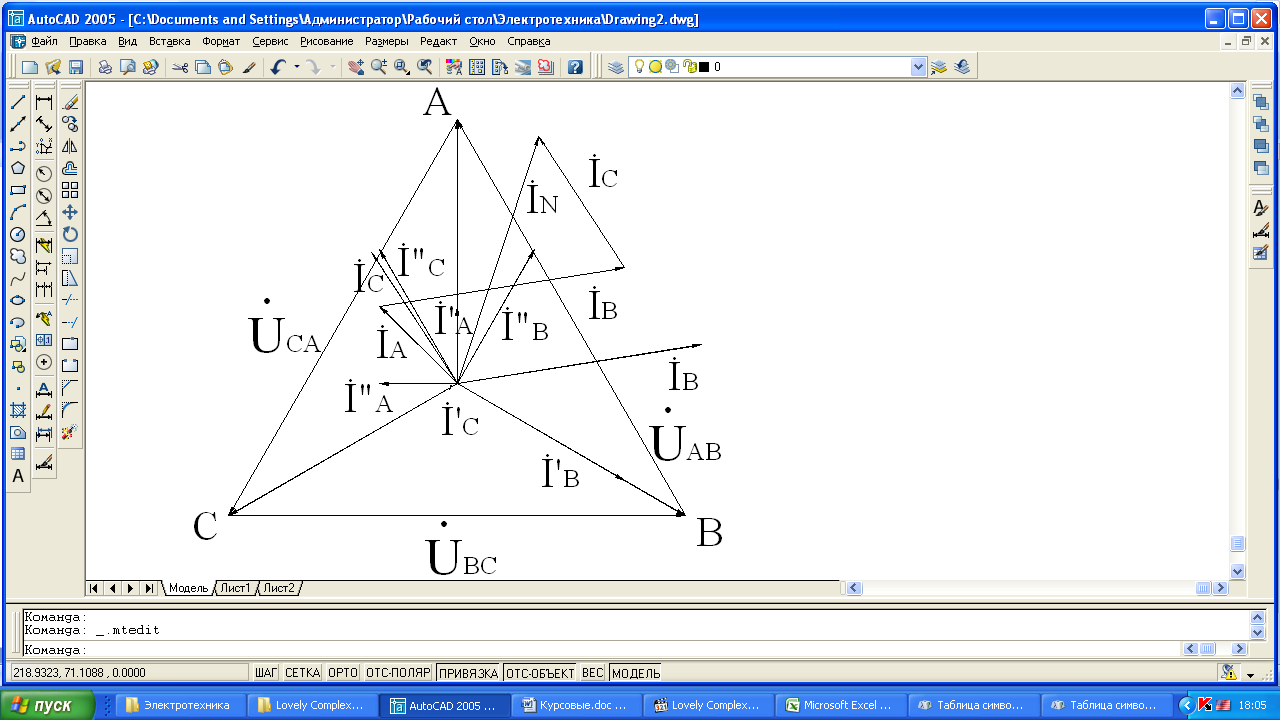
Построим в масштабе векторную диаграмму.
![]() ;
;
![]()
Расчетно-графическая работа №3

Дано:
E = 120 В;
L = 10 мГн;
C = 10 мкФ;
R1 = 30 Ом;
R2 = 70 Ом;
R3 = 100 Ом;
_____________
Рис.1 Электрическая цепь, в которой выполняется коммутация (действует ЭДС постоянного тока)
Ход работы.
-
Определим закон изменения во времени величины iL классическим методом
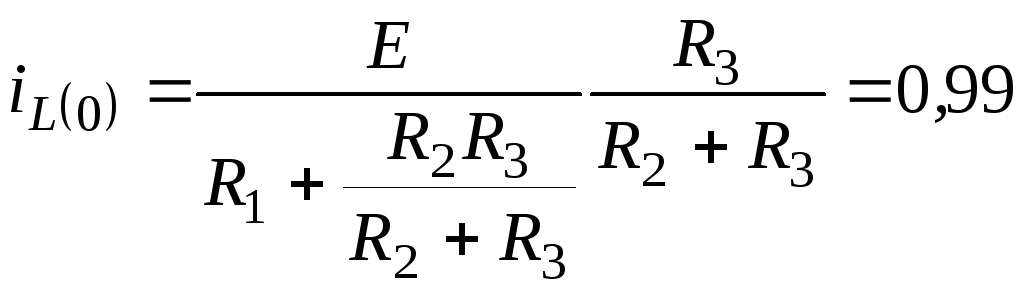 А;
А;
![]() В
В
![]() А;
А;
![]() А;
А;
![]() ;
;
![]() ;
;
![]() В
В
![]() В/Гн;
В/Гн;
 ;
;
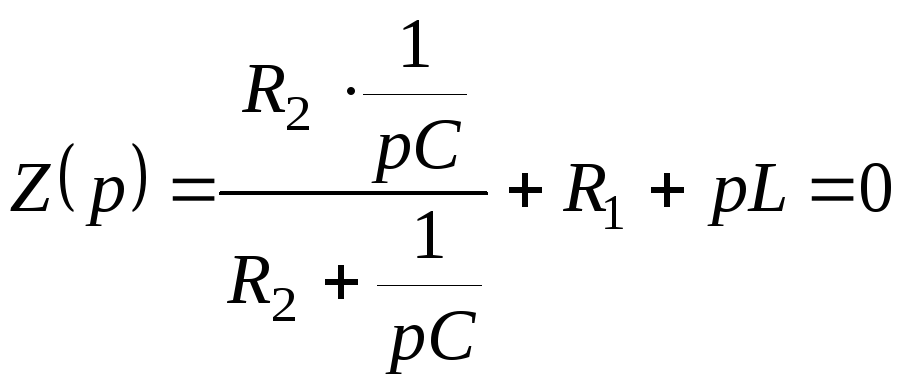 ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
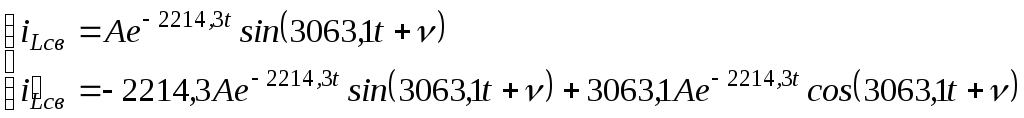
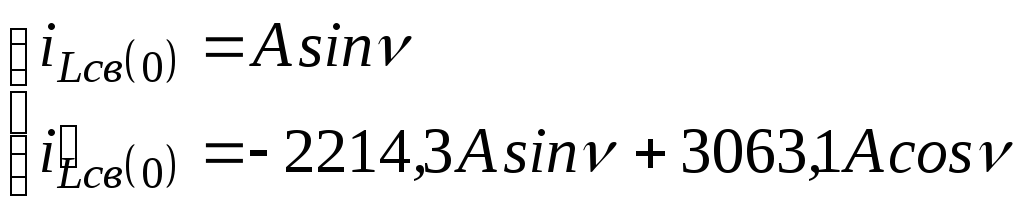
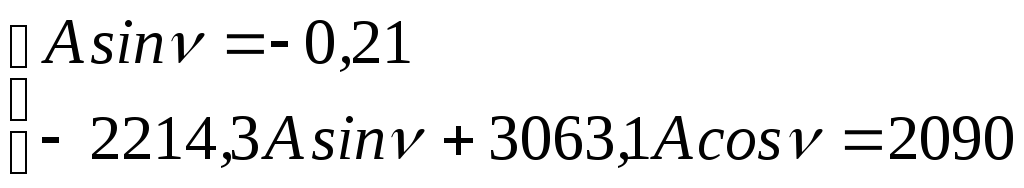
![]() ;
; ![]()
![]() В.
В.
2. Определим закон изменения во времени величины iL операторным методом
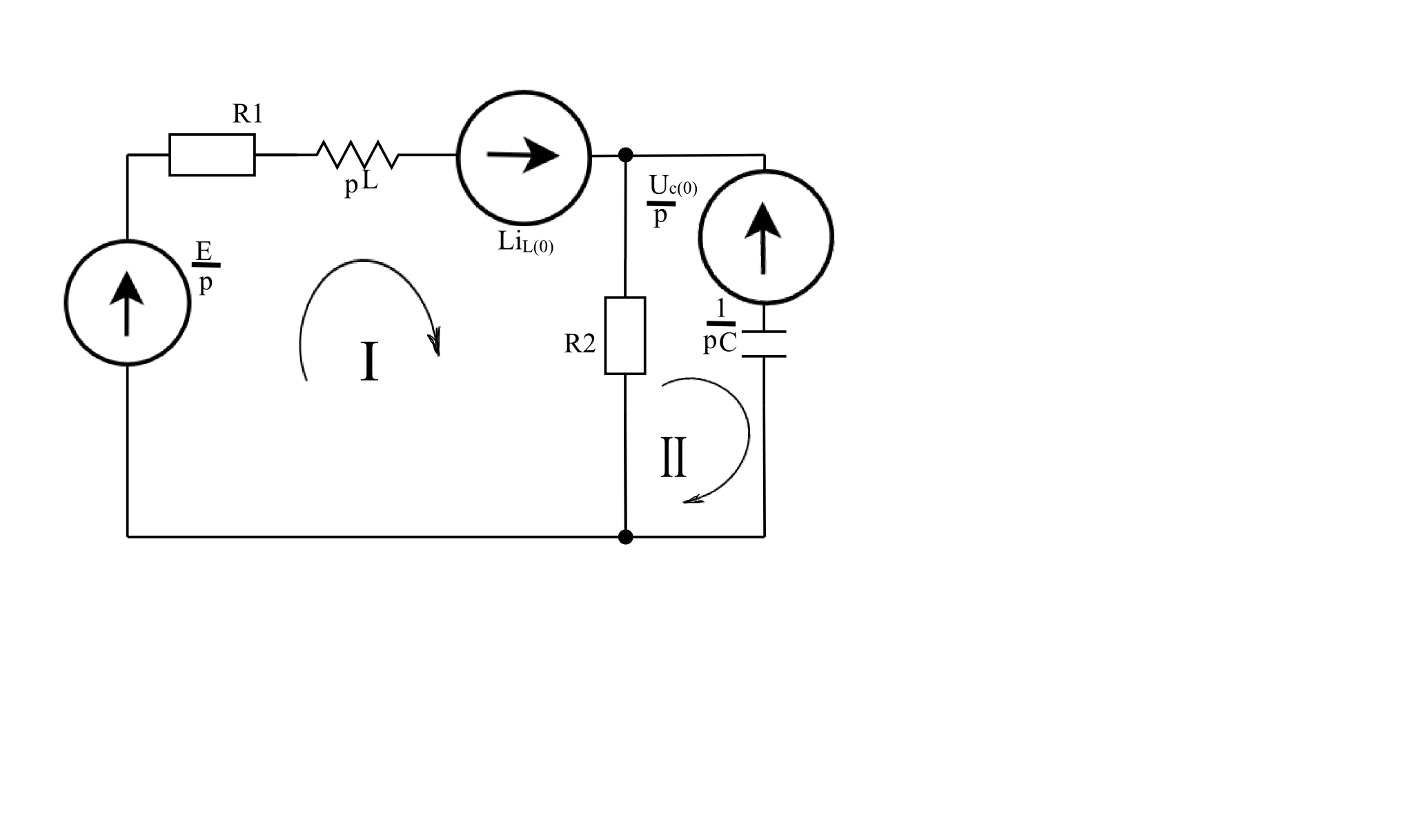
Рис.2 Операторский метод
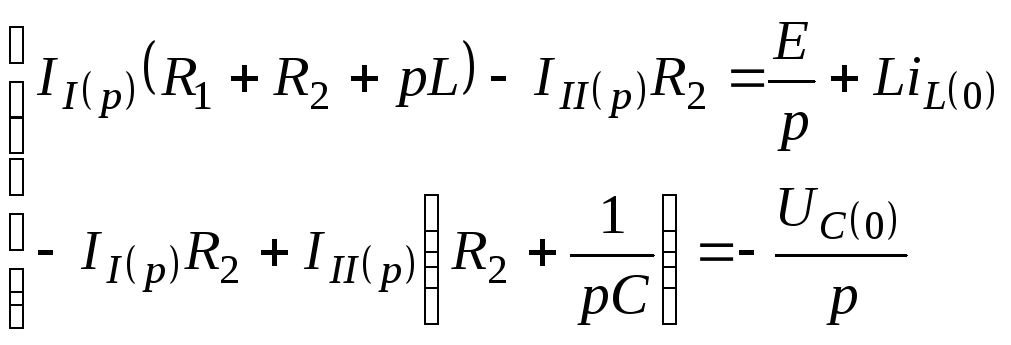
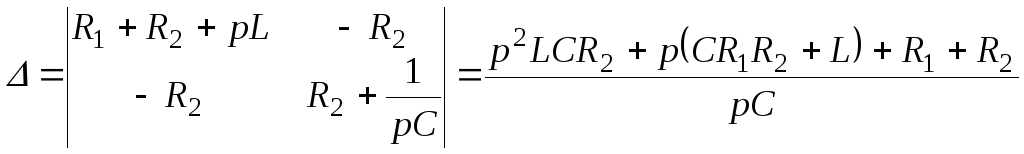
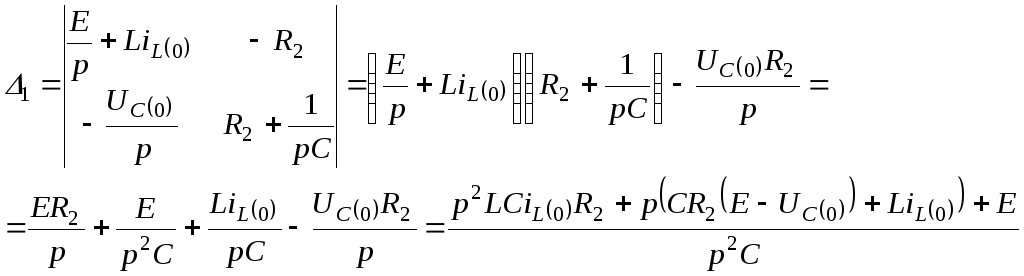
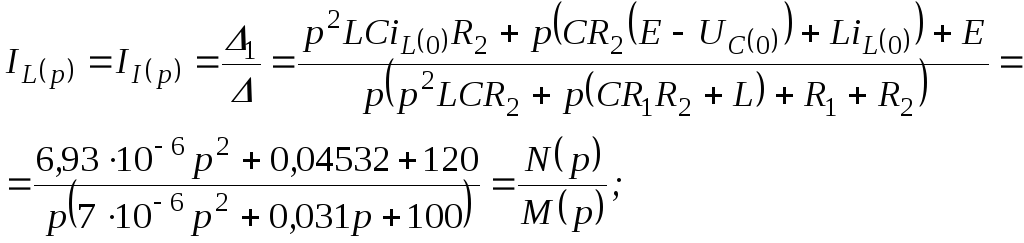
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
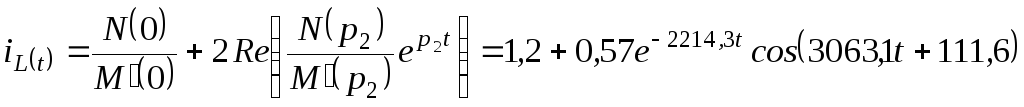 А;
А;
![]() с.
с.
-
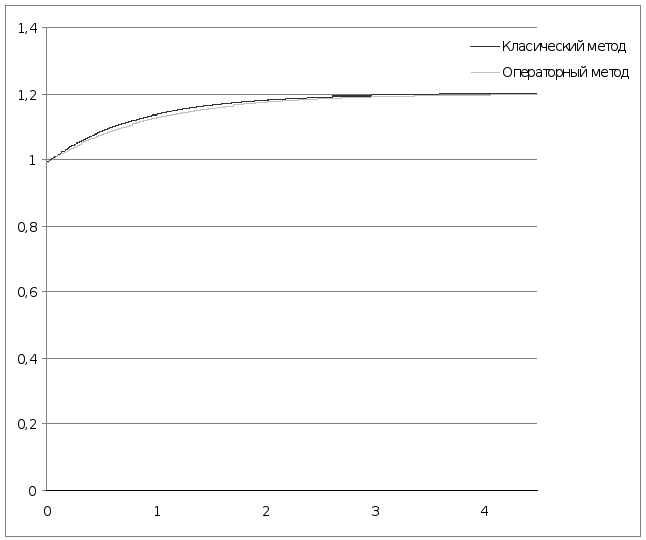
На основании полученных аналитических выражений построим график изменения искомой величины в функции времени в интервале от
t = 0 до
![]() (в программе MS Excel)
(в программе MS Excel)
![]()
![]()
