
примеры решений задач / raschet_lineynoy_cepi_postoyannogo_toka
.pdfФедеральное агентство по образованию ГОУ ВПО
Уфимский Государственный авиационный технический университет
Кафедра ТОЭ
Расчетно-графическая работа по дисциплине теоретические основы общей
электротехники
«Расчет линейной цепи постоянного тока»
Выполнил: студент гр. САПР-231 Кочергин Н. В. Проверил: Болотовский Ю. И.
Уфа-2008
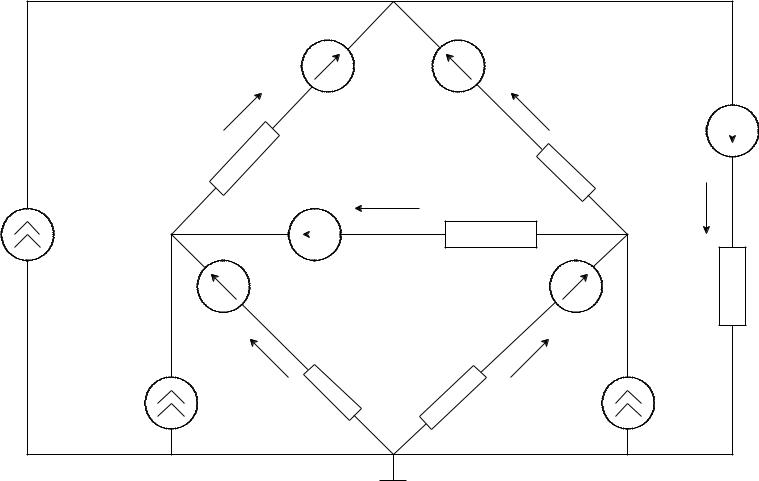
1. ОпределитьЗадание: все токи методом контурных токов
2. Определить все токи методом узловых напряжений, приняв потенциал 4-го узла равным нулю.
3. Составить баланс мощностей.
4. Определить ток I методом эквивалентного генератора.
5. Начертить в масштабе1 потенциальную диаграмму для любого контура, включающего в себя две Э.Д.С.
|
|
E4 |
2 |
E5 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
I4 |
|
|
I5 |
|
R4 |
|
|
|
E6 |
|
|
|
|
R5 |
|
Jk1 |
|
E3 |
I3 |
R3 |
I6 |
1 |
|
|
3 |
||
|
|
|
|||
|
|
E1 |
|
|
R6 |
|
|
|
|
|
E2 |
|
|
I1 |
|
|
I2 |
|
Jk2 |
R1 |
|
R2 |
Jk3 |
|
|
4 |
|||
|
|
|
|
|

Вариант P1-840541-14 |
|
|
|
|
|||
R1 |
= 90 Ом |
R4 |
= 20 Ом |
E1= -400 В |
E4= 0 В |
Jk1 |
= 3 А |
R2 |
= 80 Ом |
R5 |
= 70 Ом |
E2= 0 В |
E5= -200 В |
Jk2 |
= 0 А |
R3 |
= 90 Ом R6 |
= 30 Ом |
E3= 0 В |
E6= 0 В |
Jk3 |
= 0 А |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
E5 |
|
|
|
|
|
I4 |
|
I5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
R4 |
|
R5 |
|
|
|
|
|
|
|
|
|
|
|
Jk1 |
1 |
|
I3 |
R3 |
|
I6 |
|
|
|
|
3 |
|
||
|
|
|
|
|
R6 |
||
|
|
|
E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
I |
|
|
|
|
|
|
|
2 |
|
|
R1
R2
4
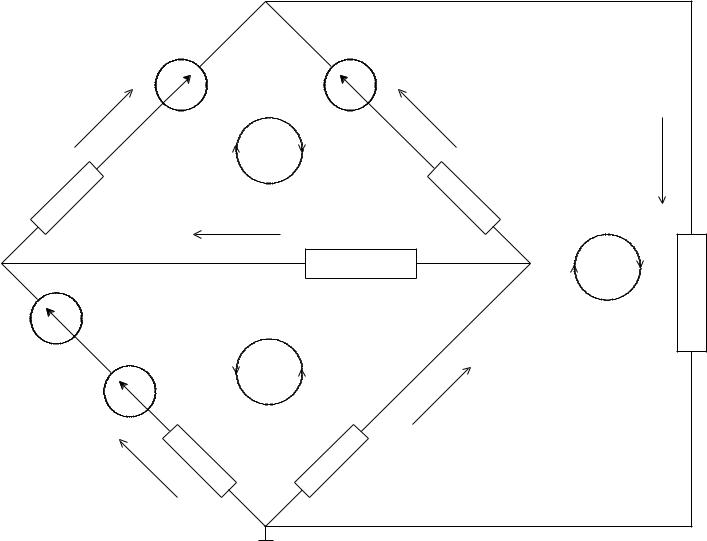
Расчет цепи методом контурных токов
|
2 |
|
|
|
E j4 |
E5 |
|
I |
4 |
I |
|
|
5 |
|
|
R4 |
I11 |
R5 |
I6 |
I |
|
||
|
|
|
|
|
3 |
R3 |
|
|
|
|
|
1 |
|
3 |
I 33 |
Ej1 |
|
|
R6 |
|
|
|
|
|
I22 |
|
|
E1 |
2 |
|
|
|
R1 |
I |
|
|
|
|
|
|
I1 |
R2 |
|
|
4 |
|
|
Проведем эквивалентное преобразование источника тока в источники ЭДС.
Введем контурные токи ; Рассчитаем собственныеIтоки:11,I22,I33
I1=-I22-Jk
I2=I33+I22
I3=I22+I11
I4=I11-Jk
I5=I33-I11
I6=I33

Запишем уравнения по методу контурных токов:
I11(R3+R4+R5)+I22R3-I33R5=-E5+Ej4
Iгде22(R1+R2+R3)+I11R3+I33R2=-E1-Ej1 I33(R2+R5+R6)+I22R2-I11R5=E5
Ej4=Jk1R4=60 В
СоставляемEj1=Jk1Rсистему1=270 Вуравнений:
180I11 |
+ |
90I22 |
- |
70I33= |
260 |
90I11 |
+ |
260I22 |
+ |
80I33= |
130 |
Составляем-70I11 + 80Iматрицу:22 - 180I11=-200
|
|
180 |
90 |
-70 |
260 |
|
|
|
|
90 |
260 |
80 |
130 |
|
Gauss получаем следующие значения |
|
|
Решив систему в программе |
|
||||
|
|
-70 |
80 |
180 |
-200 |
|
|
|
|
контурных токов: |
|
|
|
||
I11= 0,73329
I22= 0,57956
I =-1,08352
Находим33 значения реальных токов:
I1=−I22−Jk=−0,57956−3=−3,57956 A
I2=I33 I22=−1,08352 0,57956=−0,50396 A
I3=I22 I11=0,57956 0,73329=1,31285 A
I4=I11−Jk=0,73329−3=−2,26671 A
I5=I33−I11=−1,08352−0,73329=−1,81681 A
I6=I33=−1,08352 A

Расчет цепи методом узловых потенциалов
|
|
|
2 |
|
|
|
E5 |
I |
4 |
|
I |
|
|
5 |
|
|
|
|
I6 |
R4 |
|
I |
R5 |
|
|
|
|
|
|
3 |
R3 |
|
|
|
|
Jk1 1 |
|
|
3 |
|
|
|
R6 |
E1 |
|
2 |
|
|
|
R1 |
I |
|
|
|
|
|
I1 |
|
R2 |
4
Определим число уравнений и запишем их:
N=У-1=4-1=3
G11φ11-G12φ22-G13φ33=J11 |
|
|
|
||||||||||||||
-G21φ11+G22φ22-G23φ33=J11 |
|
|
|
||||||||||||||
-G31φ11-G32φ22+G33φ33=J11 |
|
|
проводимости: |
||||||||||||||
Определим1 1собственные1 1 1и взаимные1 |
|||||||||||||||||
G11= |
|
|
|
|
|
|
|
= |
|
|
|
|
|
=0,07222 См; |
|||
R1 |
R3 |
R4 |
90 |
90 |
20 |
||||||||||||
G22= |
1 |
1 |
|
1 |
|
|
1 |
|
1 |
|
1 |
=0,09761 См; |
|||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|||||
R4 |
R5 |
R6 |
20 |
30 |
70 |
||||||||||||
G33= |
1 |
1 |
|
1 |
|
|
1 |
|
1 |
|
1 |
=0,03789 См; |
|||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|||||
R2 |
R3 |
R5 |
70 |
80 |
90 |
||||||||||||
|
|
1 |
|
1 |
=0,05 См; |
|
|
||||||||||
G12=G21= |
|
= |
|
|
|
||||||||||||
R4 |
20 |
|
|
||||||||||||||
|
|
G13=G31= |
|
|
1 |
|
= |
1 |
=0,01111 См; |
|
|
|
|||||||||||||
|
|
|
R3 |
90 |
|
|
|
||||||||||||||||||
|
|
G23=G32= |
|
|
1 |
|
= |
1 |
=0,01429 См. |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
R |
|
|
70 |
|
|
|
||||||||||||||||||
ОпределимE |
узловые токи: |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J11= |
1 |
=− |
400 |
|
|
=-4,44444 A |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
R1 |
|
|
|
|
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
J22=Jk1+ |
|
E5 |
|
=3 − |
200 |
|
=0,14286 A |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
R5 |
|
70 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
J33= − |
E5 |
|
=− − |
|
200 |
|
|
=2,85714 A |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Составим матрицу и, используя программу Gauss, определяем потенциалы |
|||||||||||||||||||||||||
узлов: |
|
R5 |
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
0,72222 |
|
|
-0,05 |
|
|
|
|
-0,01111 |
|
-4,44444 |
|
|
|||||||||||
|
|
-0,05 |
|
|
|
|
|
|
|
|
|
0,9761 |
|
-0,01428 |
|
0,14285 |
|
|
|||||||
|
|
-0,01111 |
|
|
-0,014285 |
0,03789 |
|
2,85714 |
|
|
|||||||||||||||
φ11=-77,8398 В φ22=-32,5057 В φ = 40,3171 В
Используя33 обобщенный закон Ома, определим токи во всех ветвях:
I1= |
E1 φ44−φ11 |
= |
−400 0 77,8398 |
=-3,57956 A |
|||||||||||
R1 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
90 |
|
|
|
|
|
||||
I2= |
φ44−φ33 |
= |
0−40,3171 |
=-0,50396 A |
|
||||||||||
|
|
|
|
|
|||||||||||
|
|
R2 |
80 |
|
|
|
|
|
|
|
|||||
I3= |
φ33−φ11 |
= |
40,3171 77,8398 |
=1,31285 A |
|||||||||||
|
|
|
|
|
|||||||||||
|
|
R3 |
90 |
|
|
|
|
|
|
|
|||||
I4= |
φ11−φ22 |
= |
−77,8398 32,5057 |
=-2,2667 A |
|||||||||||
|
|
|
|
|
|||||||||||
|
|
R4 |
20 |
|
|
|
|
|
|
|
|||||
I5= |
|
E5 φ33−φ22 |
= |
−200 40,3171 32,5057 |
=-1,81682 A |
||||||||||
|
|
|
|
||||||||||||
|
|
R5 |
|
|
|
|
|
|
70 |
|
|
|
|
||
I6= |
φ22−φ44 |
= |
−32,5057−0 |
|
=-1,08352 A |
|
|||||||||
|
|
|
|||||||||||||
|
|
R6 |
30 |
|
|
|
|
|
|
|
|||||

|
Решение методом эквивалентного генератора |
||
|
|
2 |
|
|
|
|
E5 |
|
I |
4 |
5 |
|
|
I |
|
|
|
|
I6 |
|
R4 |
|
R5 |
|
|
3 |
|
|
|
I |
R3 |
|
|
|
|
Jk1 |
1 |
|
3 |
|
|
|
R6 |
|
|
Uxx |
2 |
|
|
I |
|
|
|
4 |
R2 |
|
|
|
|
Определим число уравнений и запишем их: |
|
||
N=У-1=4-1=3 |
|
|
|
G11φ11-G12φ22-G13φ33=J11 |
|
||
-G21φ11+G22φ22-G23φ33=J11 |
|
||
-G31φ11-G32φ22+G33φ33=J11 |
|
||

Определим собственные и взаимные проводимости:
G11= |
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
=0,06111 См |
|
|
|
|||||||||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
R3 |
R4 |
90 |
20 |
|
|
|
||||||||||||||||||||||||||||
G22= |
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
=0,09761 См |
||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||
|
R4 |
R5 |
R6 |
20 |
30 |
70 |
|||||||||||||||||||||||||||||
G33= |
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
1 |
|
1 |
=0,03789 См |
||||||||||||
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|||||||||||||||||||
|
R2 |
R3 |
R5 |
70 |
80 |
90 |
|||||||||||||||||||||||||||||
G12=G21= |
|
|
1 |
|
= |
1 |
=0,05 См |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
R4 |
20 |
|
|
|
|
|
||||||||||||||||||||||||||||
G13=G31= |
|
|
1 |
|
= |
1 |
=0,01111 См |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
R3 |
90 |
|
|
|
||||||||||||||||||||||||||||||
G23=G32= |
|
|
1 |
|
= |
1 |
|
|
=0,01429 См |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
R5 |
70 |
|
|
|
|
|
||||||||||||||||||||||||||||
ОпределимJ =0 A |
|
|
узловые токи: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
J22=Jk1+ |
|
E5 |
=3 − |
|
200 |
|
=0,14286 A |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
R5 |
|
70 |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
J33= |
− |
E5 |
|
=− − |
200 |
|
=2,85714 A |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Составим матрицу и, используя программу Gauss, определяем потенциалы |
|||||||||||||||||||||||||||||||||||
|
|
|
R5 |
|
|
|
|
|
|
|
|
|
|
|
|
70 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
узлов:0,06111 |
|
|
-0,05 |
|
|
|
|
|
|
|
-0,01111 |
|
0 |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
-0,05 |
|
|
|
|
|
|
|
|
|
|
|
|
0,09761 |
|
|
-0,01429 |
|
0,14286 |
|
|
|||||||||||||||
-0,01111 |
|
|
-0,01426 |
|
|
0,03789 |
|
2,85714 |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
φ11= 59,7455 В φ22= 48,3273 В φ33=111,127 В
Uxx=-φ11+E1=-59,7455-400=-459,745 В
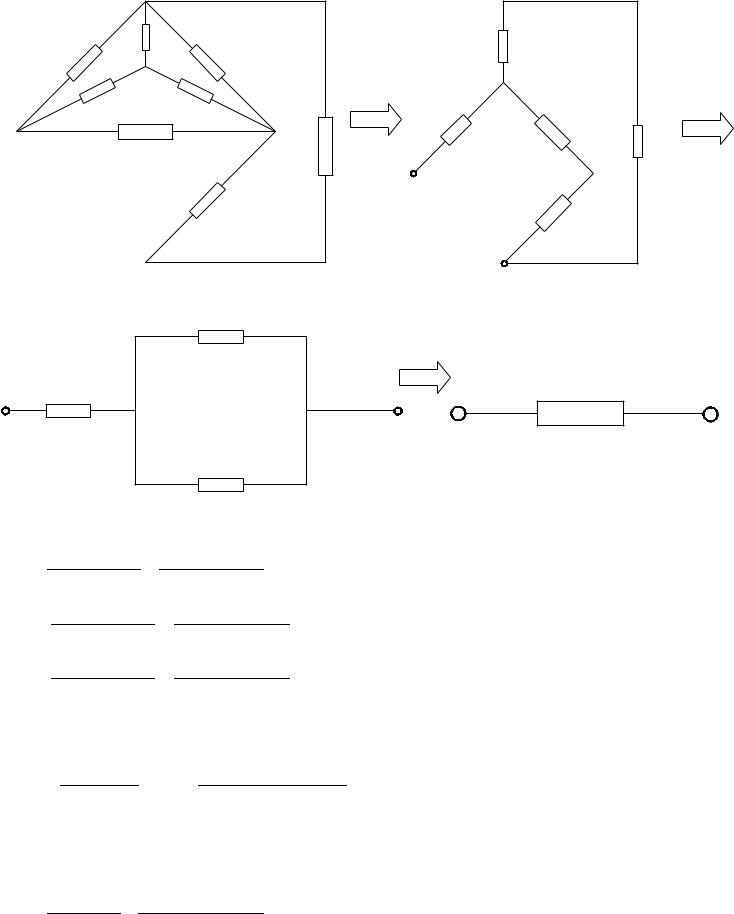
Расчет эквивалентного2 |
сопротивления |
|
|
R4 |
R8 |
|
R8 |
R5 |
|
||
|
|
|
|
R7 |
R9 |
R7 |
R9 |
1 |
|
||
|
3 |
R6 |
|
|
R3 |
R6 |
|
|
|
||
R2
R2
4
R 10
1 |
R7 |
|
|
|
|
|
4 |
1 |
4 |
|
|
|
|
|
|
|
|
|
Rэкв |
|
|
|
|
R11 |
|
|
|
|
|
R8= |
R4 R5 |
|
= |
20 70 |
=7,7778 Ом |
|
|
||
R4 R5 R3 |
|
|
|
||||||
|
20 70 90 |
|
|
|
|
|
|||
|
R3 R5 |
|
90 70 |
|
|
Ом |
|
|
|
R9= R4 R5 R3 = |
20 70 90 |
=35 |
|
|
|||||
|
R4 R3 |
|
20 90 |
|
|
Ом |
|
|
|
R7= R4 R5 R3 = |
20 70 90 |
=10 |
|
|
|||||
R10=R8 R6=7,7778 30=37,7778 |
Ом |
|
|
||||||
R11=R9 R2=35 80=115 Ом |
|
|
|
||||||
|
R10 R11 |
|
37,7778 115 |
10=38,4364 Ом |
|
||||
Rэкв = |
R10 R11 |
R7= 37,7778 115 |
|
||||||
ОпределяемU |
ток I1 : |
|
|
|
|
|
|||
I1= |
xx |
= −459,745 =−3,57956 А |
|
|
|||||
|
Rэкв R1 |
|
38,4364 90 |
|
|
|
|
|
|
