Расчет линейной цепи постоянного тока

Вариант 5

1. Определить все токи методом контурных токов

2. Определить все токи методом узловых потенциалов, приняв потенциал 4-го узла равным нулю.

3. Произвести проверку по законам Кирхгофа

4. Составить баланс мощностей

5. Определить ток I1 методом эквивалентного генератора.

6. Начертить потенциальную диаграмму для любого контура, включающего в себя две ЭДС.

Исходные данные

R1=20 Ом;

R2=90 Ом;

R3=70 Ом;

R4=60 Ом;

R5=60 Ом;

R6=10 Ом;

E1=150 В;

E3=350 В;

J2=4 А;

Электросхема:

2

E₄ E₅

R₄ R₅

I₄ I₃ I₅ R₆

E₃ R₃

J_k1 1 3

I₆

E₁ E₂

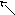
E₆

J_k2 I₁ I₂ J_k3

R₁ R₂

4

Рис. 1

В соответствии с заданными значениями сил токов источников тока и ЭДС схему можно упростить следующим образом:

Рис. 2

1) Расчет токов методом контурных токов:

Выберем произвольно направления контурных токов в цепи (Рис. 2), назовем их I_11, I_22, I_33, I₄₄ (при этом ток I₃₃ равен току источника тока ₎ и составим исходные уравнения:

Решая систему, получим:

Токи в ветвях:

Отрицательные значения полученных токов говорят о том, что заданные направления токов заданы неверно, следовательно:

2)Расчет методом узловых потенциалов:

Составим узловые уравнения:

Для первого узла:

Для второго узла:

Для третьего узла:

Подставив значения сопротивлений, решим полученную систему уравнений:

G11=1/R4+1/R1+1/R3=0,0809524

G12=-1/R4=-0,0166667

G13=-1/R3=-0,0142857

G22=1/R4+1/R5+1/R6=0,133333

G23=-1/R5=-0,0166667

G33=1/R5+1/R2+1/R3=0,0420635

I11=E1/R1+E3/R3+J2=16,5

I22==0

I33=-E3/R3=-5

Решая систему, получим:









I141+E1)/R1=-2,51347

I243)/R2=0,47851

I331+E3)/R3=1,52378

I412)/R4=3,01032

I532)/R5=-1,04527

I624)/R6=1,96504

Истинные значения:

3)Провести проверку по законам Кирхгофа:

Рис. 3

1 закон Кирхгофа.

Получаем:

Следовательно, найденные токи верны.

2 закон Кирхгофа.

Получаем:

Следовательно, найденные токи верны.

4) Проверить баланс мощности:

Для расчета мощности необходимо знать напряжение на источнике тока . Оно равно разности потенциалов между точками 1 и 4, то есть из задания 2 это 220,173 В.

Составим баланс мощностей:

Следовательно, баланс мощности сходится.

5) Определить ток I1 методом эквивалентного генератора.

Рассмотрим часть схемы, подключенную к исследуемой ветви с током I1, в качестве эквивалентного источника ЭДС Еэк сопротивлением Rэк:

1 1

E₁ E_эк E_эк

I₁

R₁ R_эк R_эк

4

4

Рис. 4 Рис. 5

Eэк вычислим с отключенной первой ветвью:

Найдем потенциал узла 1 методом узловых потенциалов:

Найдем эквивалентное сопротивление, заменив источники ЭДС короткозамкнутыми участками:

2

R₄ R₅

R₆

R₃

1 3

R₂

4

Рис. 6

Преобразуем схему на Рис. 6 в схему на Рис. 7 по формулам преобразования треугольника в звезду.

R6

R2

Рис. 7

Эквивалентное сопротивление равно:

Ток I1 найдем из схемы 4 по закону Ома:

Истинное значение I1 2,5 А.

6) Начертить потенциальную диаграмму для любого контура, включающего в себя две ЭДС.

2

R₄ R₅

I₄ I₅ R₆

E₃ R₃

1 3

6 I₆

E₁ I₃

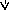
5

J_k2 I₁ I₂

R₁ R₂

4

Рис. 8

Добавим точки 5 и 6 для нахождения потенциала в них. Значения потенциалов точек 1 и 2 возьмем из второго задания. Точку 4 в начало координат и с нее начнем отсчет: