примеры решений задач / вариант 4raschet

Федеральное агентство по образованию

Сибирская государственная автомобильно-дорожная академия

(СибАДИ)

Кафедра “Электротехника”

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА

“Расчет параметров электрических цепей постоянного тока средствами EXCEL”

Вариант 4 – 2г

Работу выполнил:

студент гр. 21 АД

Омск – 2005

1. Исходные данные.

схема 2г

Номер варианта	Параметры цепи
	Ом						В
4	20	80	100	35	150	100	100	250

Исходная схема

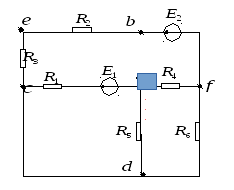
2. Решение задачи с использованием законов Кирхгофа.

Законы Кирхгофа применяем для исходной схемы.

По первому закону Кирхгофа

для узла :

для узла :

для узла :

По второму закону Кирхгофа

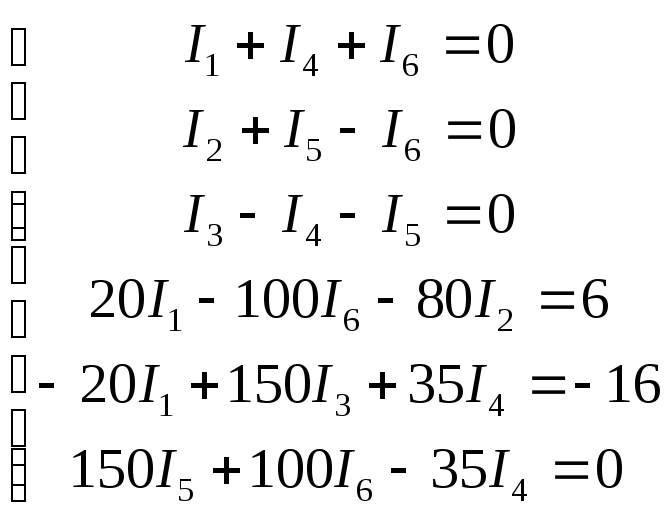
Составляем матрицу коэффициентов и решаем ее в EXCEL

;

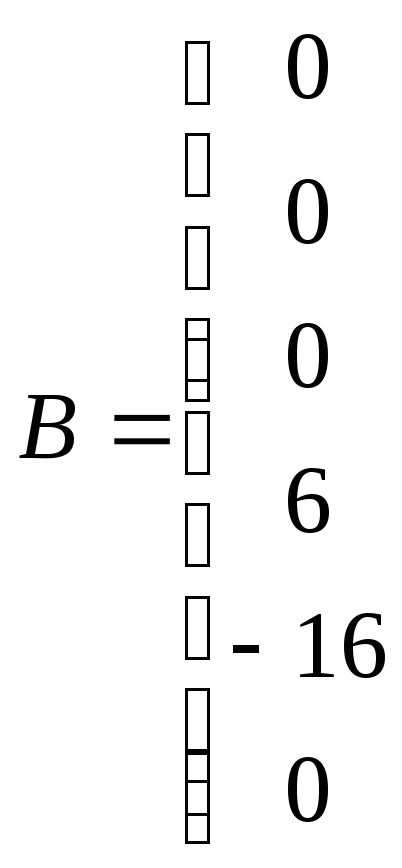
, умножаем обратную матрицу на матрицу столбец и получаем искомые значения сил токов в цепи

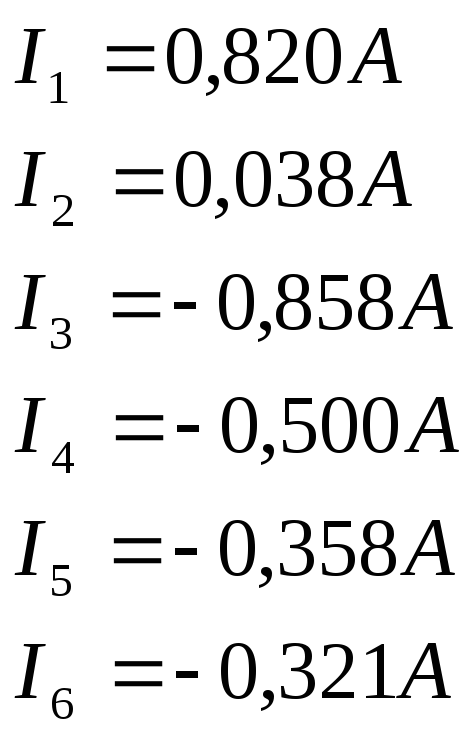
3. Метод преобразования.

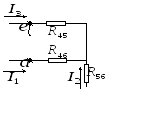
Для того, чтобы значения токов ,, не изменились величины преобразованных сопротивлений должны быть

Ом

Ом

Ом

Преобразованная схема имеет вид

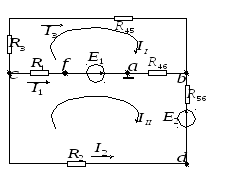
4. Метод контурных токов.

Для преобразованной схемы:

Пусть направление обхода контура совпадает с направлением контурного тока, тогда

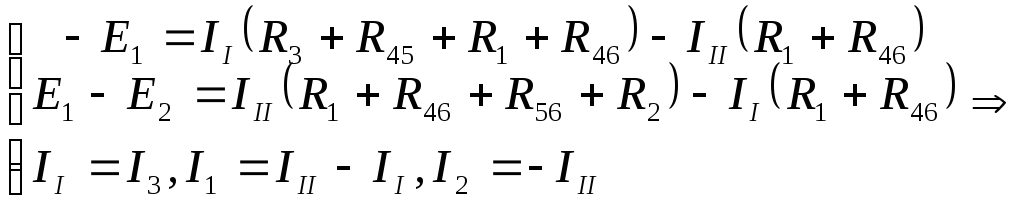
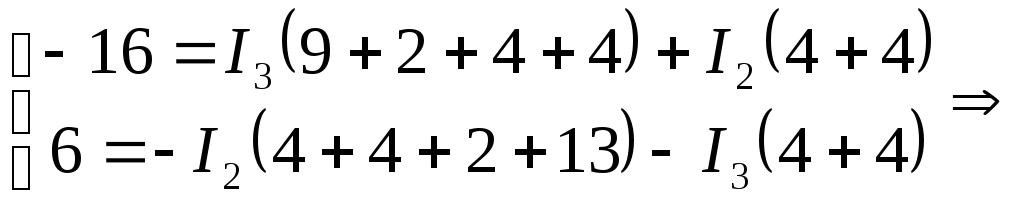
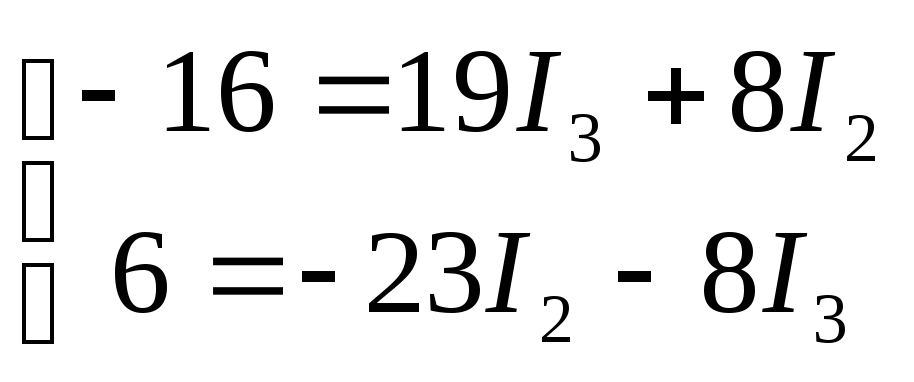
Решая систему уравнений, получаем, что

Для исходной схемы:

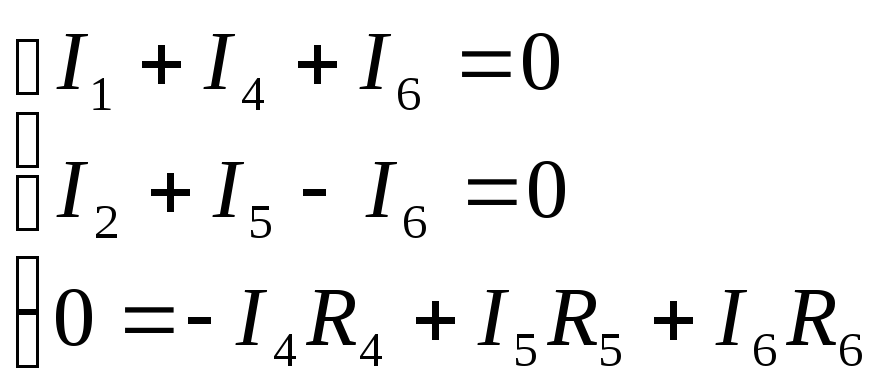
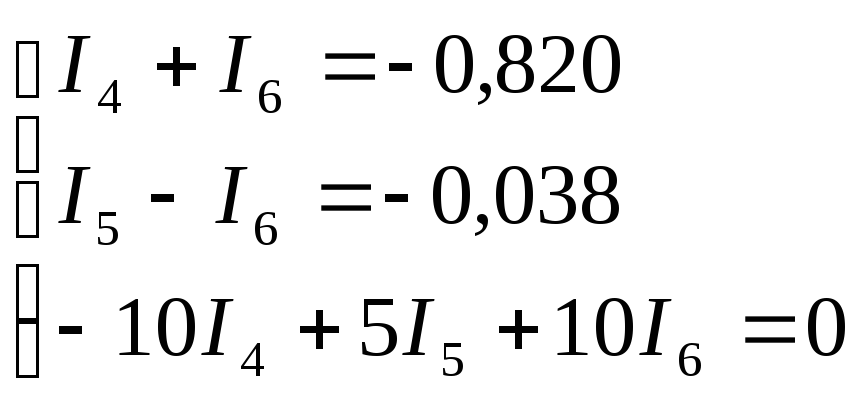
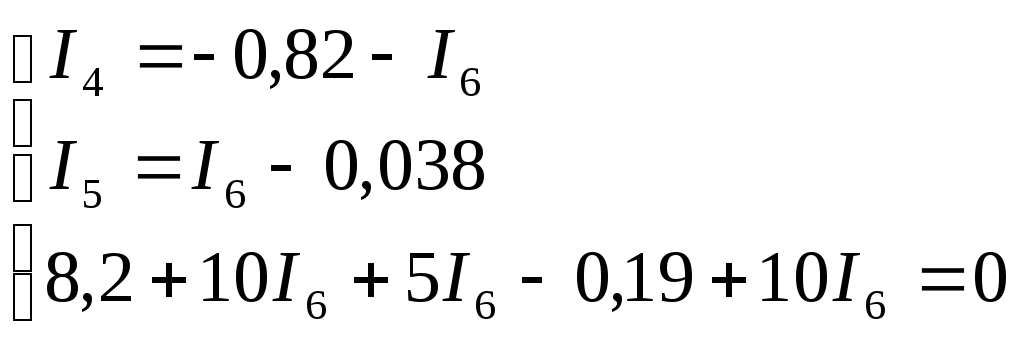
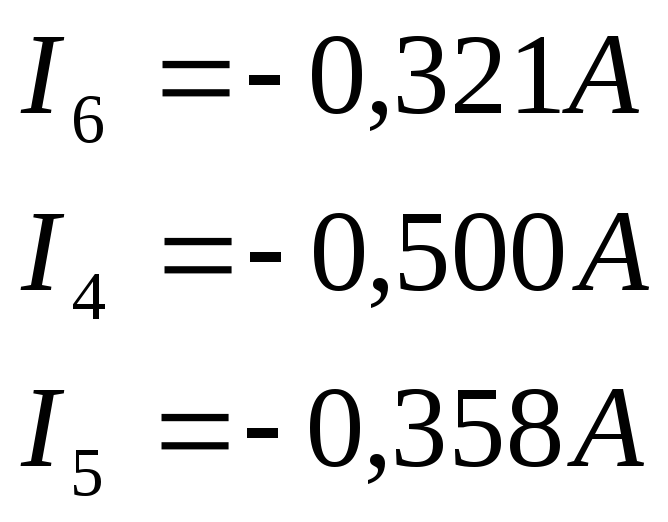
Значения токов, рассчитанных по двум методам, одинаковы.

5. Метод узловых потенциалов.

Для исходной схемы:

; ; ; ; ;

Составляем систему уравнений для узловых потенциалов

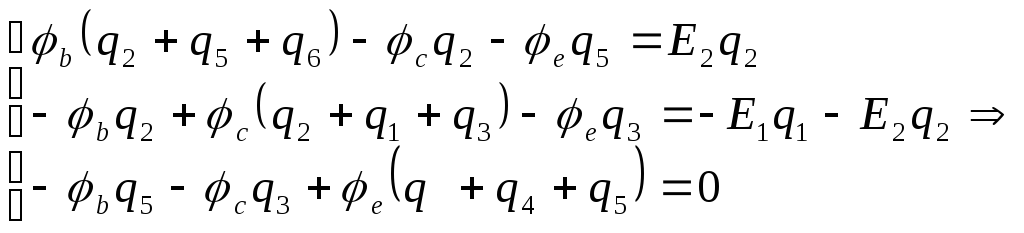
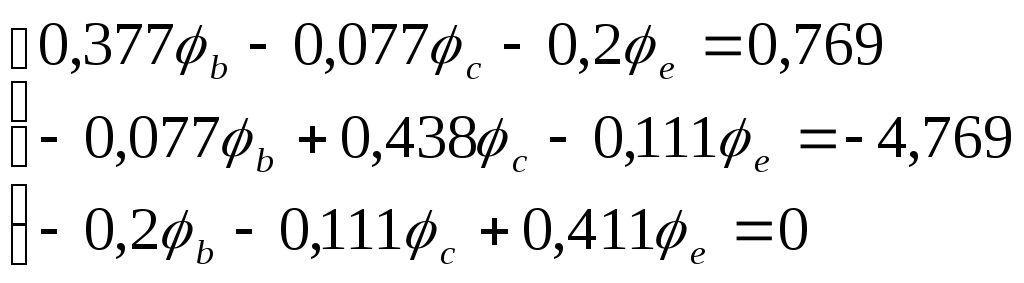
Решая систему, получаем

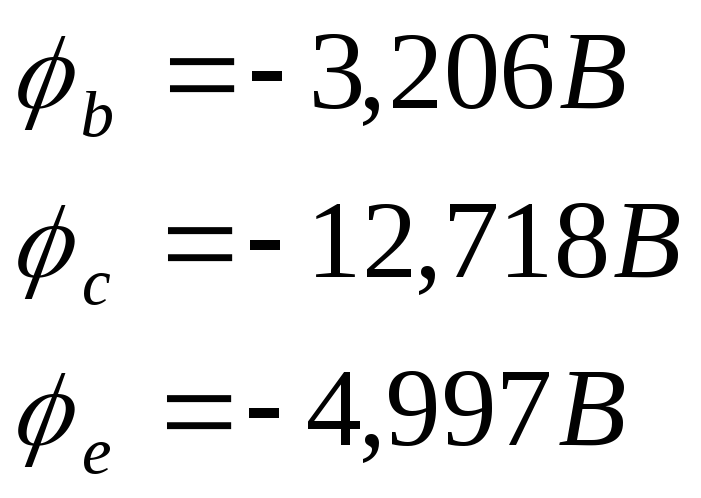
По закону Ома определяем токи:

6.Метод эквивалентного генератора.

Необходимо рассчитать ток , для расчета напряжения используем следующую схему

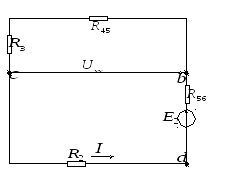
По закону Ома

Для нижней части внешнего контура

Ом

Эквивалентная схема для расчета тока

По закону Ома

7.Баланс мощностей.

Для исходной схемы:

8. Потенциальная диаграмма.

Составляем потенциальную диаграмму для контура :

R₆

R₂

R₁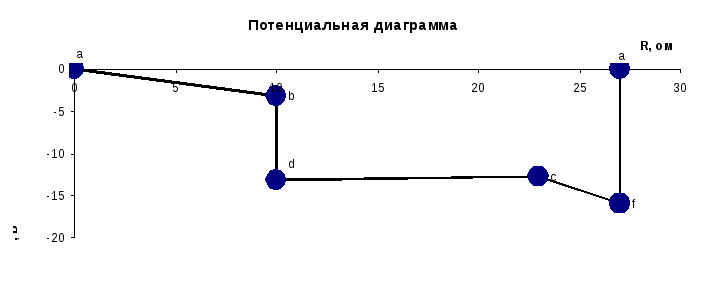

Расчеты в EXCEL

1) По законам Кирхгофа

Исх. Матрица Матрица столбец

	1	0		0	1		0	1
	0	1		0	0		1	-1
	0	0		1	-1		-1	0
	20	80		0	0		0	-150
	-20	0		100	35		0	0
	0	0		0	-35		100	150

0

0

0

6

-16

0

Обратная Матрица Ответ

0,72118	0,383378	0,36193	0,029491	-0,04021	-0,00429
0,117962	0,337802	0,193029	-0,05094	-0,02145	-0,02895
0,160858	0,27882	0,44504	0,021448	0,061662	0,033244
0,1437	-0,09759	-0,25576	-0,00751	0,028418	-0,03164
0,017158	0,376408	-0,2992	0,028954	0,033244	0,064879
0,135121	-0,28579	-0,10617	-0,02198	0,011796	0,035925

0,8203753

0,0375335

-0,857909

-0,499732

-0,358177

-0,320643

2) Метод контурных токов Исх. Матрица Матр. Столбец

	-23			-8
	8			19

6

-16

Обратная матрица Ответ

	-0,05094		-0,02145
	0,021448		0,061662

0,037534

-0,857909

3) Метод узловых потенциалов

Исх. Матрица Матрица столбец

	0,377		-0,077		-0,2
	-0,077		0,438		-0,111
	-0,2		-0,111		0,411

0,769

-4,769

0

Обратная матрица Ответ

	4,208612		1,35137		2,412956
	1,351373		2,88477		1,436701
	2,412956		1,4367		3,995292

-3,208

-12,72

-4,996