
примеры решений задач / analiz_elektricheskoy_cepi_sinusoidalnogo_toka
.doc
Порядок выполнения работы:
Часть 1. Анализ электрической цепи синусоидального тока
-
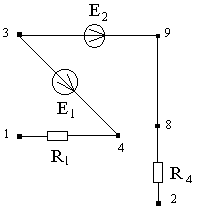
Согласно индивидуальному заданию, составить схему электрической цепи, обозначить все элементы, задать направления токов.
-
Составить систему уравнений по законам Кирхгофа в дифференциальной и комплексной форме.
-
Определить токи в ветвях схемы методом контурных токов.
-
Записать мгновенные значения токов.
-
Проверить правильность расчетов по законам Кирхгофа.
-
Составить баланс активных и реактивных мощностей.
-
Составить топографическую диаграмму напряжений, совместив ее с векторной диаграммой токов ветвей схемы.
-
Определить токи в ветвях цепи при введении индуктивной связи между двумя индуктивностями.
Часть 2. Анализ электрической цепи периодического несинусоидального тока.
1) Определить для исходной схемы мгновенные значения токов в ветвях при замене синусоидальных источников напряжений на периодические несинусоидальные.
-
Схема электрической цепи.
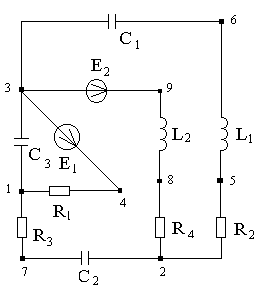
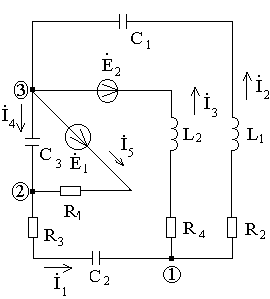
R1=70 Ом, R2=40 Ом, R3=50 Ом, R4=70 Ом,
L1=5010-3 Гн, L2=4010-3 Гн,
C1=5010-6 Ф, С2=5010-6 Ф, C3=8010-6 Ф,
E1=50120 В, E2=20250 В
f=50 Гц
2. Система уравнений по законам Кирхгофа.
Уравнения в дифференциальной форме:
1 закон Кирхгофа:
-
i1–i2–i3=0
-
–i1+i4+i5=0
2 закон Кирхгофа:
-
i5R1–
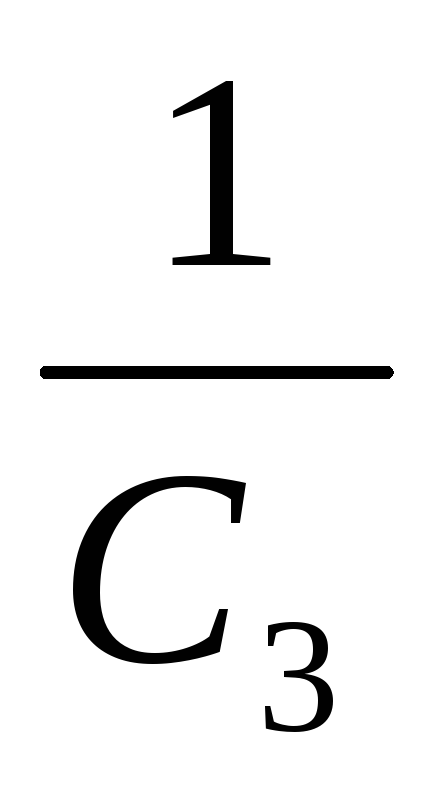
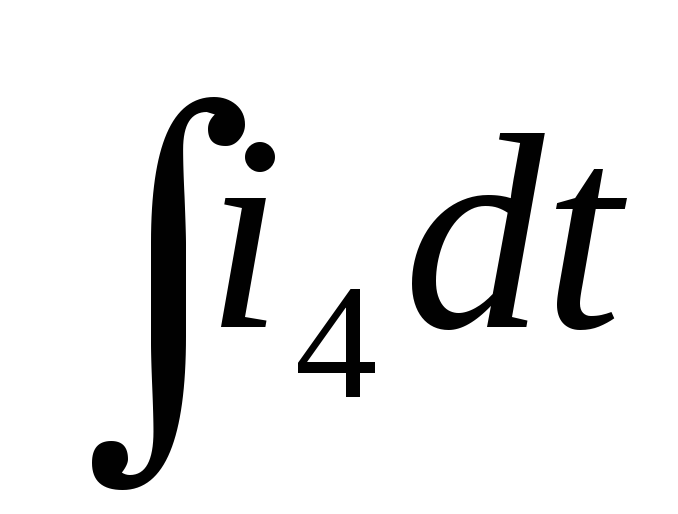 =e1
=e1 -
–L2
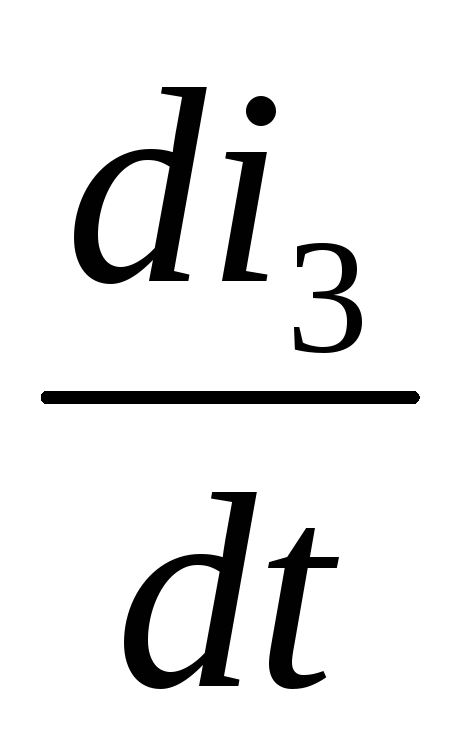 –i3R4–
–i3R4–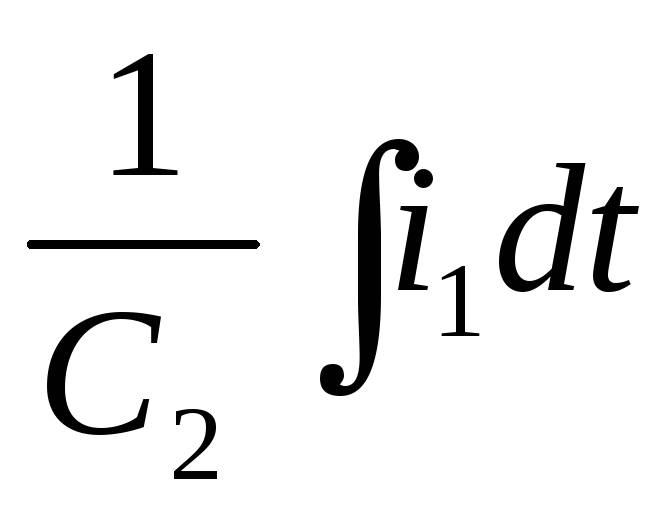 –i1R3–i5R1=e2–e1
–i1R3–i5R1=e2–e1 -
–
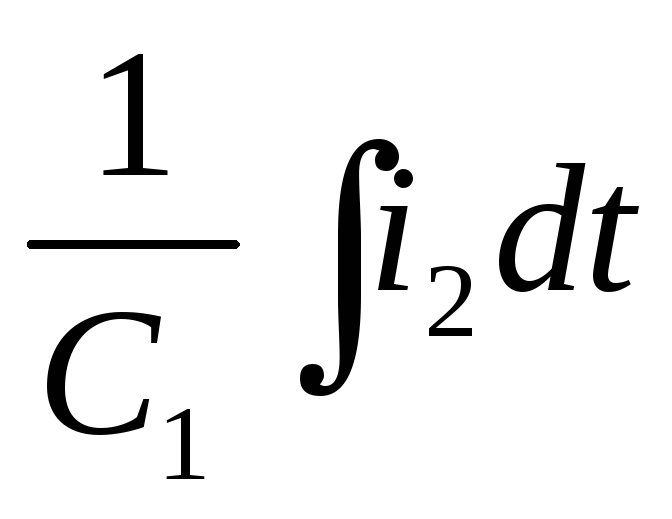 –L1
–L1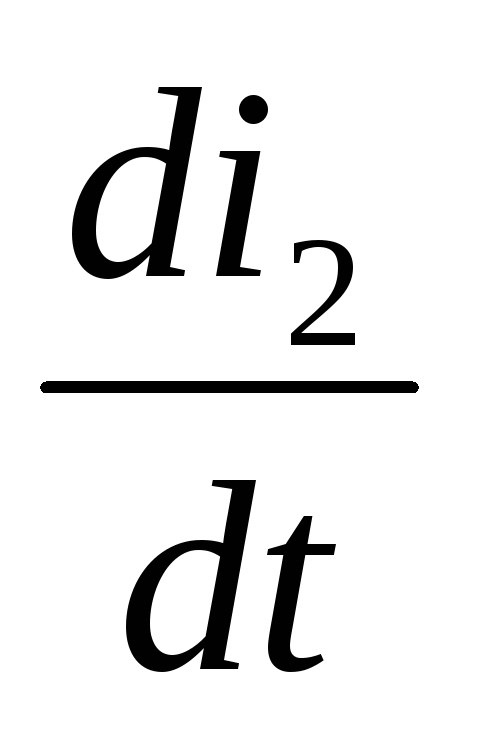 –i2R2+i3R4+L2
–i2R2+i3R4+L2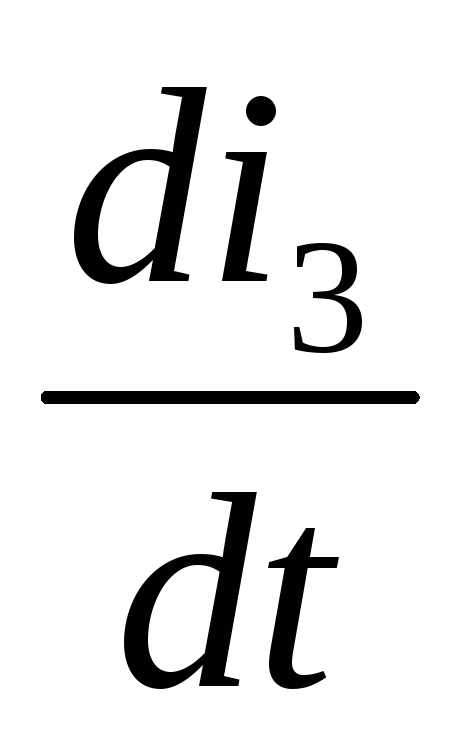 =–e2
=–e2
Уравнения в комплексной форме:
1 закон Кирхгофа:
1)
![]() –
–![]() –
–![]() =0
=0
2)
–![]() +
+![]() +
+![]() =0
=0
2 закон Кирхгофа:
I)
![]() R1–
R1–![]()
![]() =
=![]()
-
–jL2
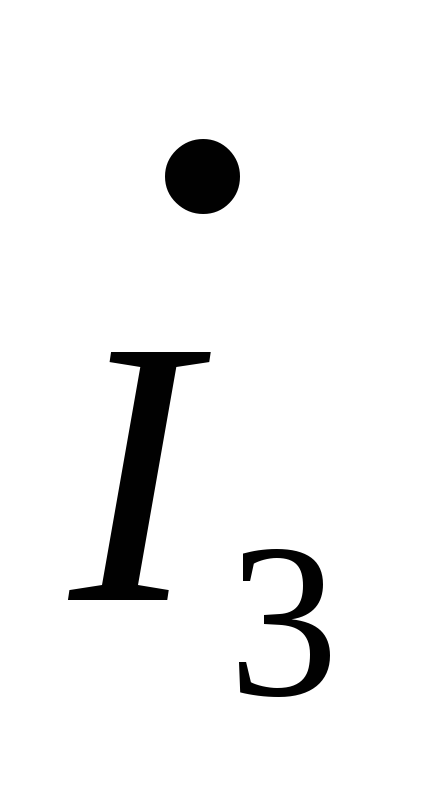 –
–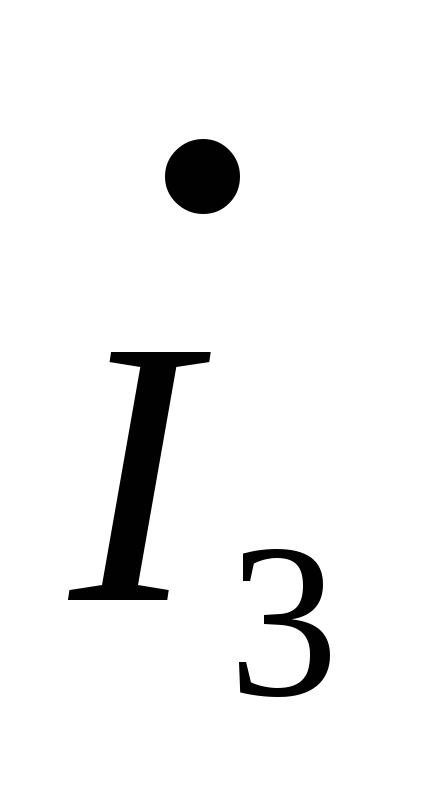 R4–
R4–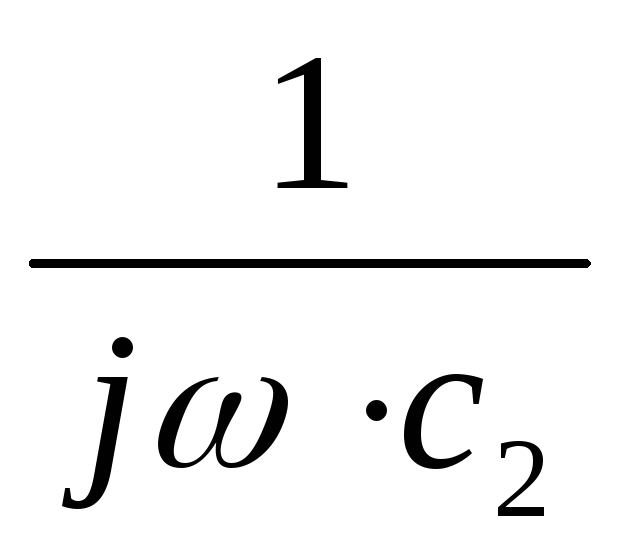
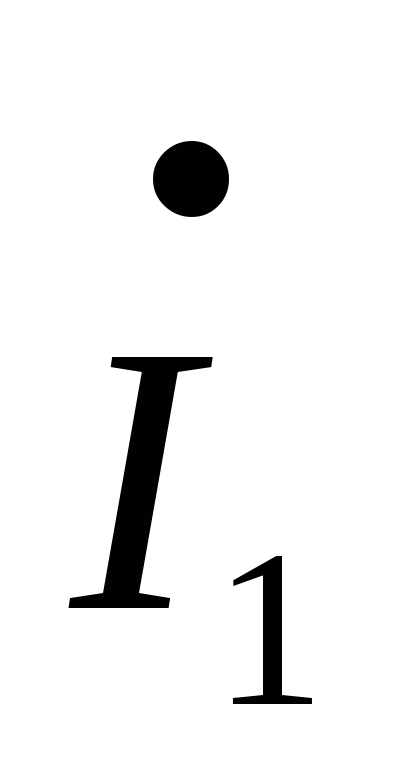 –
–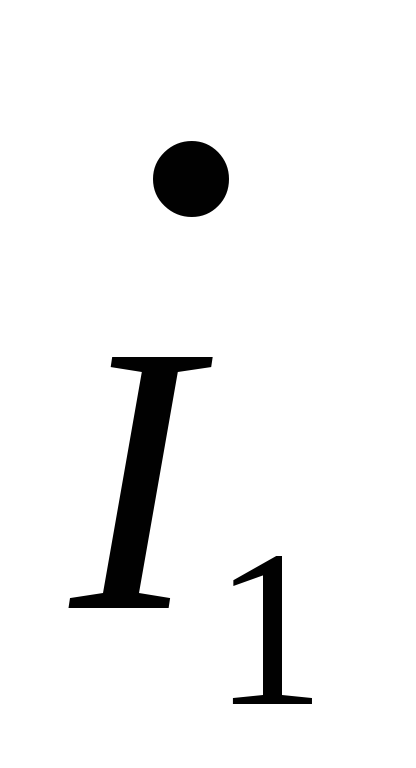 R3–
R3–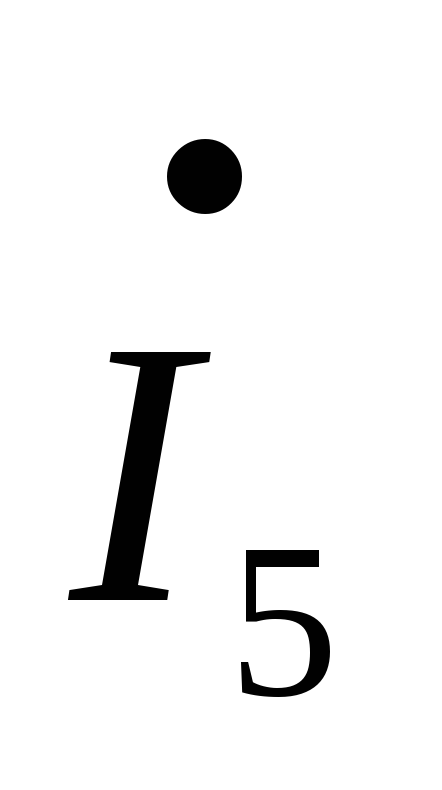 R1=
R1=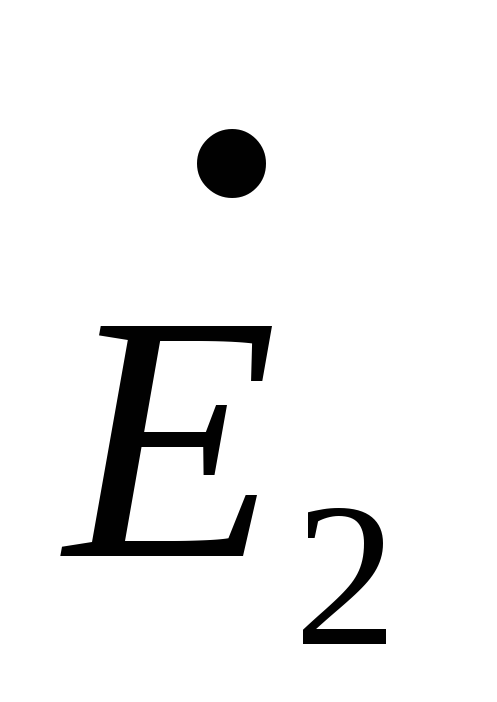 –
–
-
–
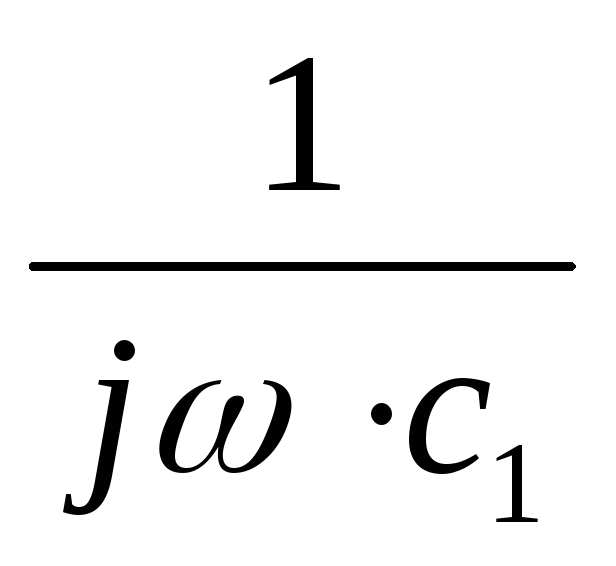
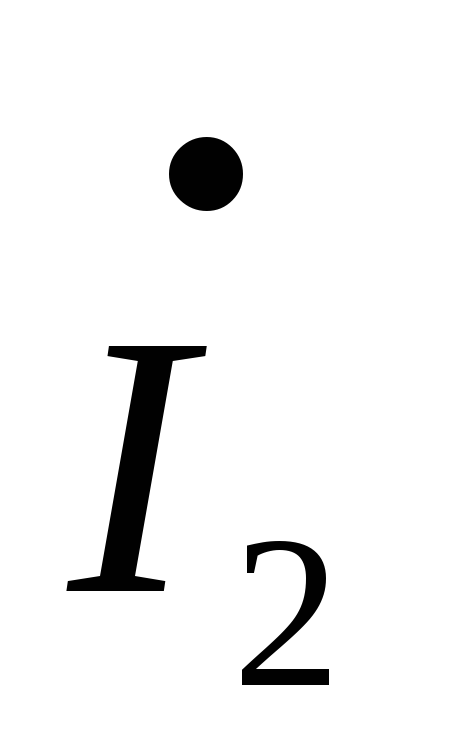 –
jL1
–
jL1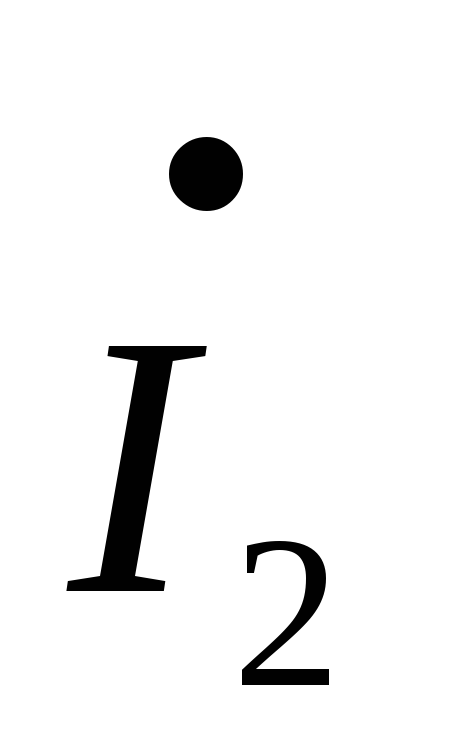 –
–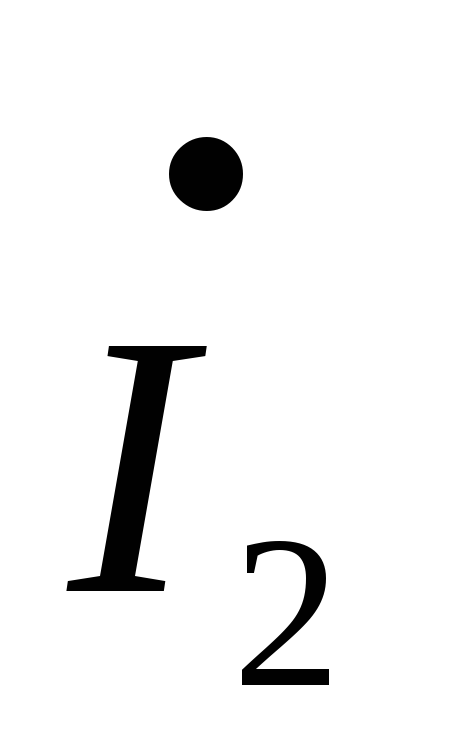 R2+
R2+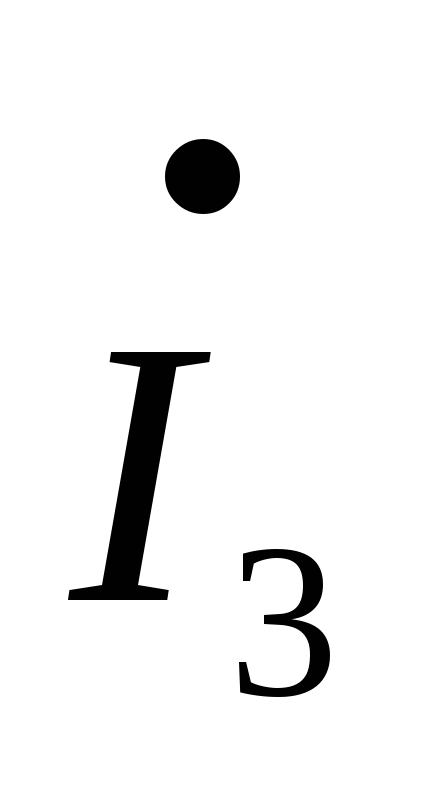 R4+
jL2
R4+
jL2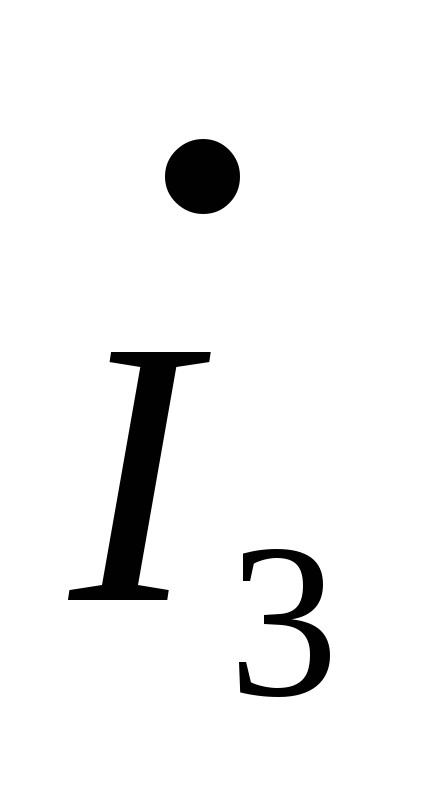 =–
=–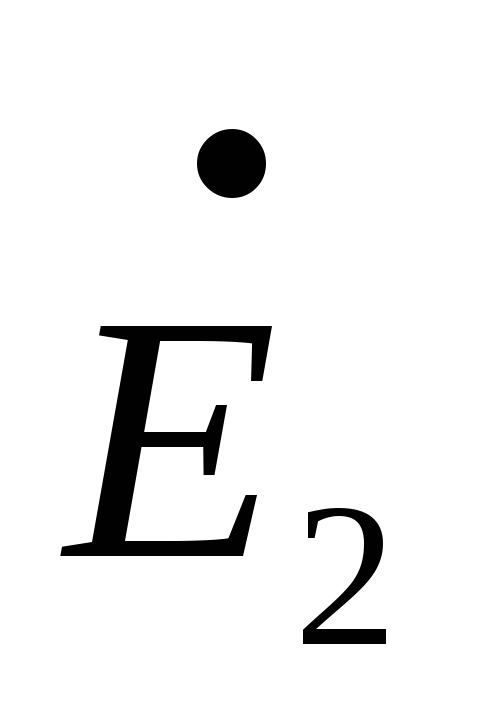
Предварительные вычисления:
=2f
=23,1450=314 (рад/с)
E1=50120=cej=a+bj
a=ccos=50(–0,5)=–25
b=csin=50(0,866)=43.3
E1=–25+43,3j (B)
E2=20250=cej=a+bj
a=ccos=20(–0,342)=–6,84
b=csin=20(–0,94)=–18,8
E2=–6,84–18,8j (B)
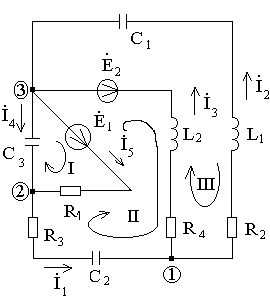
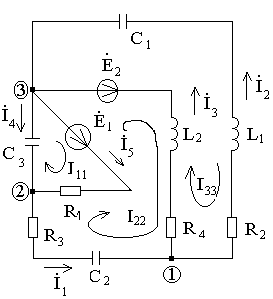
3. Определение токов в ветвях схемы методом контурных токов.
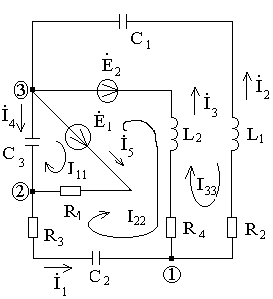
Обход контуров – по часовой стрелке.
1)
![]() (R1+
(R1+![]() )–
)–![]() R1=
R1=![]()
2)
![]() (jL2+R4+
(jL2+R4+![]() +R3+R1)–
+R3+R1)–
![]() R1–
R1–![]() (jL2+R4)=
(jL2+R4)=
![]() –
–![]()
3)
![]() (
(![]() +
jL1+R2+R4+
jL2)–
+
jL1+R2+R4+
jL2)–
![]() (
jL2+R4)=–
(
jL2+R4)=–
![]()
1)
![]() (70–j
(70–j![]() )–
)–![]() 70=–25+43.3j
70=–25+43.3j
2)
–![]() 70+
70+![]() (j3144010-3+70–
(j3144010-3+70–![]() +50+70)–
+50+70)–
![]() (j3144010-3+70)=–6,84–18,8j+25–43,3j
(j3144010-3+70)=–6,84–18,8j+25–43,3j
3)
0![]() –
–![]() (j3144010-3+70)+
(j3144010-3+70)+
![]() (–
(–![]() +j3145010-3+
+40+70+j3144010-3)=6,84+18,8j
+j3145010-3+
+40+70+j3144010-3)=6,84+18,8j
Решая систему уравнений, получаем:
![]() =–0.407+0.156j
=–0.407+0.156j
![]() =0,039–0,231j
=0,039–0,231j
![]() =0,094+0,058j
=0,094+0,058j
![]() =–
=–![]() =–0,039+0,231j=0,23ej(-8025+180)
=–0,039+0,231j=0,23ej(-8025+180)
![]() =–
=–![]() =–0,094–0,058j=0.11ej3140+180
=–0,094–0,058j=0.11ej3140+180
![]() =
=![]() –
–![]() =0,055+0,289j=0.29ej7913
=0,055+0,289j=0.29ej7913
![]() =–
=–![]() =0,407–0,156j=0.43ej(-2058)
=0,407–0,156j=0.43ej(-2058)
![]() =
=![]() –
–![]() =–0,446+0,387j=0.59ej(-4057+180)
=–0,446+0,387j=0.59ej(-4057+180)
4. Мгновенные значения токов.
i=![]() sin(t+)
sin(t+)
i1=0.324sin(314t–8025+180)
i2=0.155sin(314t+3140+180)
i3=0.409sin(314t+7913)
i4=0.606sin(314t–2058)
i5=0.832sin(314t–4057+180)
5. Проверка правильности расчетов
по законам Кирхгофа.
1 закон Кирхгофа:
1)
![]() –
–![]() –
–![]() =0
=0
–0,039+0,231j+0.094+0.058j–0.055–0.289j=0
0+0j=0
2)
–![]() +
+![]() +
+![]() =0
=0
0.039–0.231j+0.407–0.156j–0.446+0.387j=0
0+0j=0
2 закон Кирхгофа:
I)
![]() R1–
R1–![]()
![]() =
=![]()
(–0.446+0.387j)70+![]() (0.407–0.156j)=–25+43.3j
(0.407–0.156j)=–25+43.3j
–25.02+43.29j–25+43.3j
-
–jL2
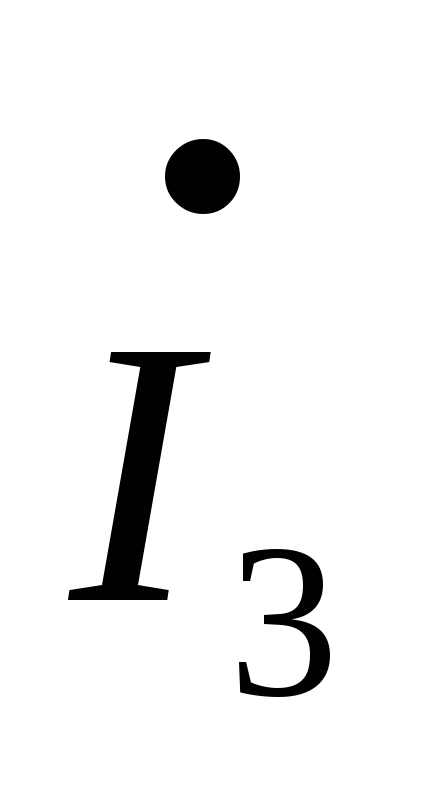 –
–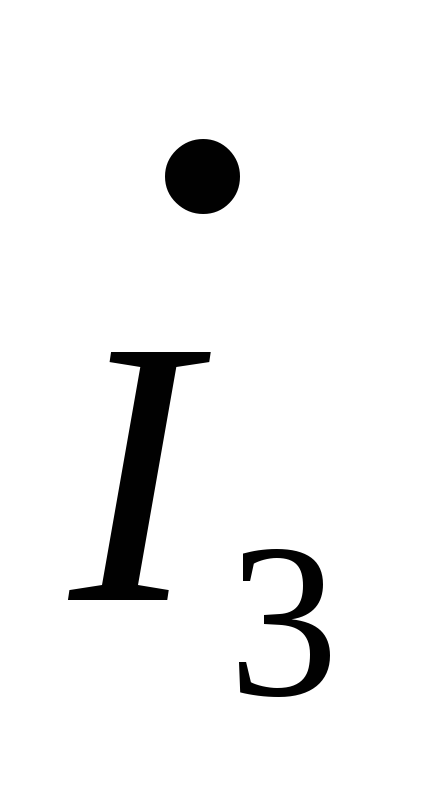 R4–
R4–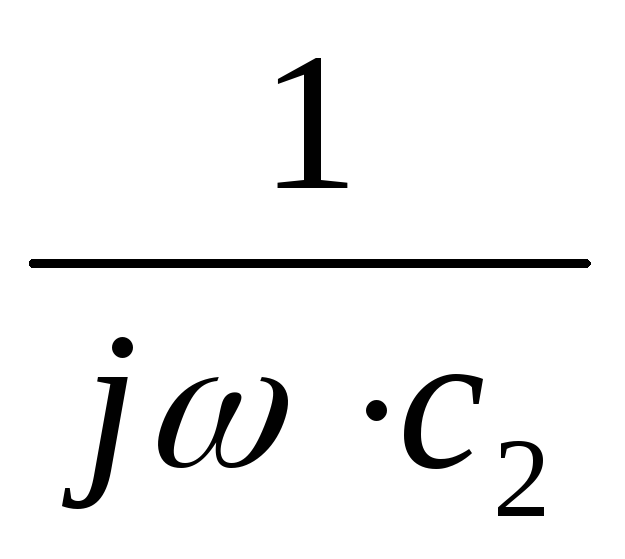
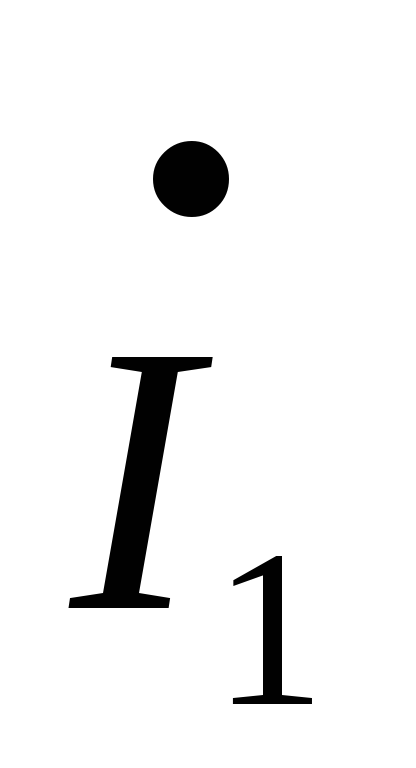 –
–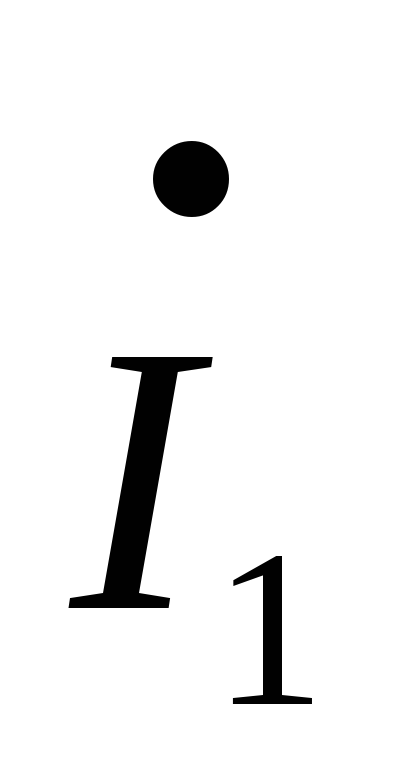 R3–
R3–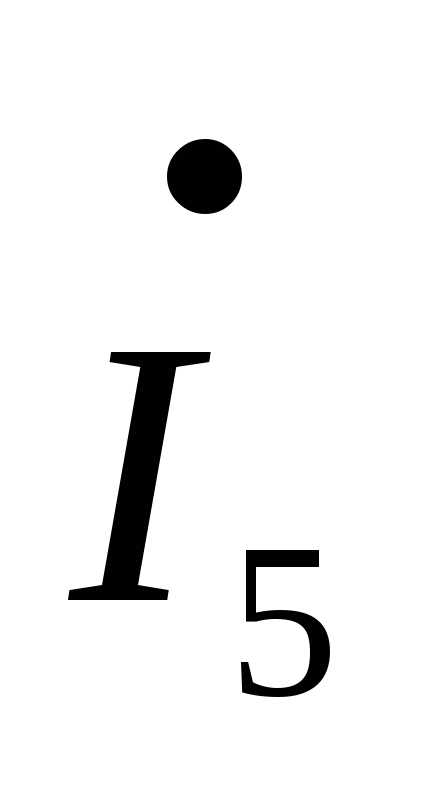 R1=
R1=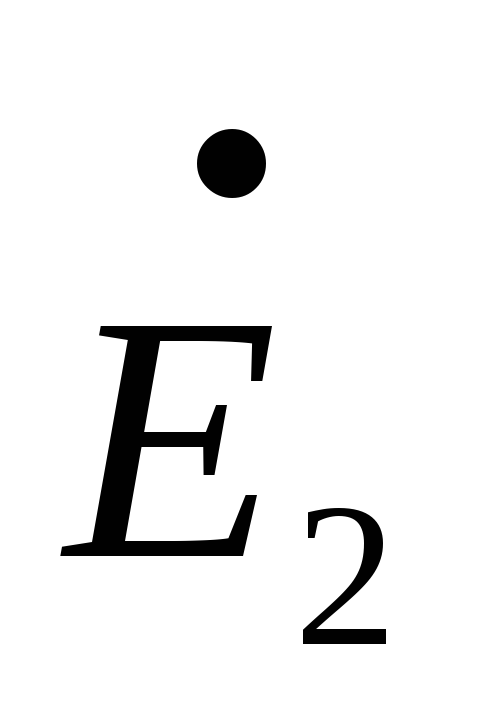 –
–
(–0.039+0.231j)(j![]() –50)–(0.055+0.289j)
(70+j3144010-3)–(–0.446+0.387j)
70=–6.84–18.8j+25–43.3j
–50)–(0.055+0.289j)
(70+j3144010-3)–(–0.446+0.387j)
70=–6.84–18.8j+25–43.3j
18.24–62j18.16–62.1j
III)
–![]()
![]() –
jL1
–
jL1![]() –
–![]() R2+
R2+![]() R4+
jL2
R4+
jL2![]() =–
=–![]()
(–0.094–0.058j)(j![]() –j3145010-3–40)+(0.055+0.289j)
(70+j3144010-3)=6.84+18.8j
–j3145010-3–40)+(0.055+0.289j)
(70+j3144010-3)=6.84+18.8j
6.764+18.728j6.84+18.8j
6. Баланс активных и реактивных мощностей.
![]()
![]() =
=![]()
![]() =(–25+43.3j)(–0.445–0.386j)–(–6.84–18.8j)(–0.054––0.285j)=33,7–10,575j
=(–25+43.3j)(–0.445–0.386j)–(–6.84–18.8j)(–0.054––0.285j)=33,7–10,575j
![]()
![]() =0,59270+0,23250+0,29270+0,11240=33,383
=0,59270+0,23250+0,29270+0,11240=33,383
![]() =
=![]() =
=![]()
![]() =j3144010-30,292+j3145010-30,112=1,246j
=j3144010-30,292+j3145010-30,112=1,246j
![]() =
=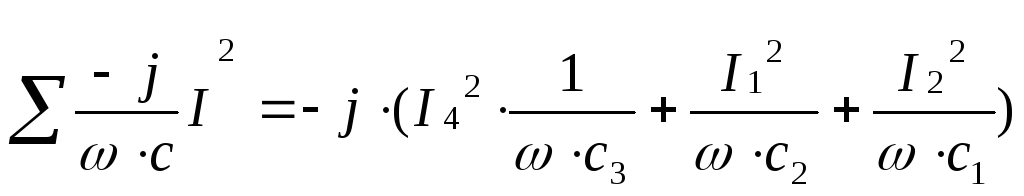
![]() =
=![]() (0,432
(0,432![]() +0,232
+0,232![]() +0,112
+0,112![]() )=–11,5j
)=–11,5j
33,7–10,575j=33,383–11,5j+1,246j
33,7–10,575j33,383–10,254j
Баланс активных и реактивных мощностей сходится, законы Кирхгофа выполняются, следовательно, токи найдены верно.
-
Топографическая диаграмма напряжений
и векторная диаграмма токов ветвей схемы.
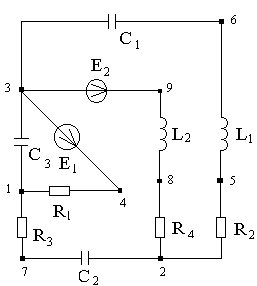
1)
![]() 3=0
В
3=0
В
![]() 4=
4=![]()
![]() 4=–25+43,3j
В
4=–25+43,3j
В
![]() 1=
1=![]() 4–
4–![]()
![]() 1=–25+43,3j–70(–0,446+0,387j)=6,22+16,21j
В
1=–25+43,3j–70(–0,446+0,387j)=6,22+16,21j
В
![]() 3=
3=![]() 1–
1–![]()
![]() 3=6,22+16,21j–
3=6,22+16,21j–![]() =0,02+0,01j В
=0,02+0,01j В
![]() 30
В
30
В
2)
![]() 9=
9=![]()
![]() 9=–6,84–18,8j В
9=–6,84–18,8j В
![]() 8=
8=![]() 9+
9+![]()
![]() 8=–6.84–18.8j+j3144010-3(0.055+0.289j)=
8=–6.84–18.8j+j3144010-3(0.055+0.289j)=
=–10.47–18.11j В
![]() 2=
2=![]() 8+
8+![]()
![]() 2=–10,47–18,11j+70(0,055+0,289j)=–6,62+2,12j В
2=–10,47–18,11j+70(0,055+0,289j)=–6,62+2,12j В
![]() 7=
7=![]() 2–
2–![]()
![]() 7=–6,62+2,12j–
7=–6,62+2,12j–![]() (–0,039+0,231j)=8,08+4,6j
В
(–0,039+0,231j)=8,08+4,6j
В
![]() 1=
1=![]() 7+
7+![]()
![]() 1=8,08+4,6j+50(–0,039+0,231j)=6,13+16,15j
В
1=8,08+4,6j+50(–0,039+0,231j)=6,13+16,15j
В
3)
![]() 6=
6=![]()
![]() 6=(–0,094–0,058j)
6=(–0,094–0,058j)![]() =–3,7+5,6j В
=–3,7+5,6j В
![]() 5=
5=![]() 6+
6+![]()
![]() 5=–3.7+5.9j+j3145010-3(–0.094–0.058j)=–2.79+4.43j
В
5=–3.7+5.9j+j3145010-3(–0.094–0.058j)=–2.79+4.43j
В
![]() 2=
2=![]() 5+
5+![]()
![]() 2=–2,79+4,43j+40(–0,094–0,058j)=–6,55+2,11j
В
2=–2,79+4,43j+40(–0,094–0,058j)=–6,55+2,11j
В
Синий цвет – контур 3-4-1-3
Зеленый цвет – контур 3-9-8-2-7-1-3
Красный цвет – контур 3-6-5-2-7-1-3
-
Определение токов в ветвях цепи
при наличии индуктивной связи
между двумя индуктивностями.
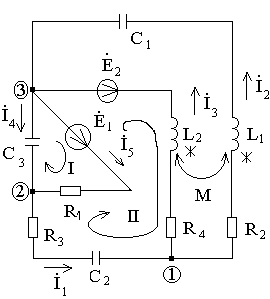
Ток
![]() проходит по контуру 2-7-1-3-6-5-2.
проходит по контуру 2-7-1-3-6-5-2.
Обход контуров по часовой стрелке.
M=K![]()
M=0.58![]() =0.0259
Гн
=0.0259
Гн
1)
![]() (R1+
(R1+![]() )–
)–![]() R1+
R1+![]() =
=![]()
2)
![]() (jL2+R4+
(jL2+R4+![]() +R3+R1)–
+R3+R1)–
![]() R1+
R1+![]() (R3+
(R3+![]() +jM)=
=
+jM)=
=![]() –
–![]()
3)
![]() (
(![]() +
jL1+R2+R3+
+
jL1+R2+R3+![]() +
+![]() )
–
)
–![]() (
(![]() +R3)+
+
+R3)+
+![]() (
(![]() )+
)+![]() jM=0
jM=0
1)
![]() (70–j
(70–j![]() )–
)–![]() 70–
70–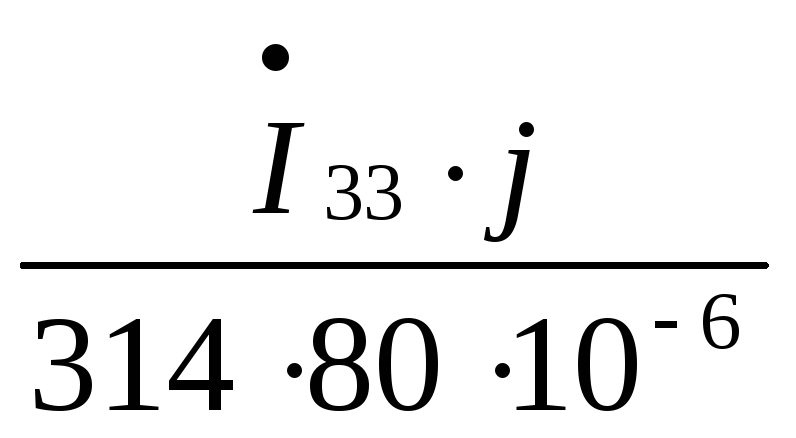 =–25+43.3j
=–25+43.3j
2)
–![]() 70+
70+![]() (j3144010-3+70–
(j3144010-3+70–![]() +50+70)–
+50+70)–
![]() (50–
(50– ![]() )=–6,84–18,8j+25–43,3j
)=–6,84–18,8j+25–43,3j
3)
![]() (–
(–![]() )+
)+![]() (–
(–![]() +50+j3140.0259)+
+50+j3140.0259)+
+![]() (–
(–![]() +j3145010-3+40+50–
+j3145010-3+40+50–![]() –
–![]() )=0
)=0
Решая систему уравнений, получаем:
![]() =–0,475+0,095j
=–0,475+0,095j
![]() =–0,034–0,296j
=–0,034–0,296j
![]() =0,071+0,052j
=0,071+0,052j
В скобках указан путь через узлы, по которым проходит ток.
![]() (1-7-2)=–
(1-7-2)=–![]() –
–![]() =–0,037+0,244j=0,246ej(–8122+180)
=–0,037+0,244j=0,246ej(–8122+180)
![]() (2-5-6-3)=–
(2-5-6-3)=–![]() =–0.071–0.052j=0.087ej3613+180
=–0.071–0.052j=0.087ej3613+180
![]() (2-8-9-3)=–
(2-8-9-3)=–![]() =0,034+0,296j=0.298ej8326
=0,034+0,296j=0.298ej8326
![]() (3-1)=–
(3-1)=–![]() –
–![]() =0.404–0.147j=0.429ej(–20)
=0.404–0.147j=0.429ej(–20)
![]() (3-4-1)=
(3-4-1)=![]() –
–![]() =–0.441+0.391j=0.589ej(–4133+180)
=–0.441+0.391j=0.589ej(–4133+180)
Часть 2. Определение мгновенных значений токов в ветвях при замене синусоидальных источников напряжений на периодические несинусоидальные.
Размыкая ветви с конденсаторами и замыкая ветви с индуктивностями, получаем схему, в которой нет ни одного замкнутого контура. Следовательно, все токи по нулевой гармонике будут равны 0. Токи по первой (основной) гармонике найдены в пункте (3).
Расчет токов по третьей гармонике:
Обход контуров – по часовой стрелке.
1)
![]() (R1+
(R1+![]() )–
)–![]() R1=
R1=![]()
2)
![]() (jL2+R4+
(jL2+R4+![]() +R3+R1)–
+R3+R1)–
![]() R1–
R1–![]() (jL2+R4)=
(jL2+R4)=
![]() –
–![]()
3)
![]() (
(![]() +
jL1+R2+R4+
jL2)–
+
jL1+R2+R4+
jL2)–
![]() (
jL2+R4)=–
(
jL2+R4)=–
![]()
1)
![]() (70–j
(70–j![]() )–
)–![]() 70=–39,39–6,94j
70=–39,39–6,94j
2)
–![]() 70+
70+![]() (j9424010-3+70–
(j9424010-3+70–![]() +50+70)–
+50+70)–
–![]() (j9424010-3+70)=3,47+19,69j
+39,39 +6,94j
(j9424010-3+70)=3,47+19,69j
+39,39 +6,94j
3)
0![]() –
–![]() (j9424010-3+70)+
(j9424010-3+70)+
![]() (–
(–![]() +j9425010-3+
+40+70+j9424010-3)=–3,47–19,69j
+j9425010-3+
+40+70+j9424010-3)=–3,47–19,69j
