
Лекции Просолупов
.pdf
Определение 26.4 . Пусть 1, 2 . Произведением перестановок 2 и 1 называют композицию этих функций: 2 1( ) = 2( 1( )), = 1, .
Докажем, что произведение перестановок есть перестановка. Очевидно, что 21 : {1, ..., } → {1, ..., }. Покажем инъективность. Пусть , {1, ..., } и ̸= . Поскольку 1 инъективна, 1( ) ̸= 1( ), а поскольку инъективна 2, 2( 1( )) ̸=2( 1( )). Следовательно,
2 1( ) = 2( 1( )) ̸= 2( 1( )) = 2 1( ).
То есть, 2 1 — инъективна, а, значит, является перестановкой.
§27. Группа перестановок
Определение 27.1 . Группой называется непустое множество с определенной на нем бинарной операцией , которая не выводит из множества и
удовлетворяет трем аксиомам:
1 ассоциативность: для любых , , верно, что
( ) = ( );
2 наличие нейтрального элемента: существует такой элемент , что для любого справедливо
= = ;
3 наличие обратного элемента: для любого элемента найдется такой элемент −1 , что
−1 = −1 = .
Произведение перестановок ассоциативно:
(( 3 2) 1)( ) = ( 3 2)( 1( )) = 3( 2( 1( ))) = = 3(( 2 1)( )) = ( 3 ( 2 1))( )
Нейтральным элементом
(
перестановка =
1 2 ...
1 2 ...
верно = = .
для |
множества будет служить тождественная |
). |
Легко заметить, что для любой перестановки |
Для любой перестановки , как для любой биективной функции, существует обратная функция −1: −1 = −1 = . Для любых {1, ..., } ( ) =
−1( ) = . Функция −1, обратная для биективной функции , также будет биективной функцией: −1 : {1, ..., } → {1, ..., }. То есть, −1 .
Замечание 27.2 . Заметим, что обратная перестановка −1 для данной перестановки единственна. Действительно, если бы существовала еще одна такая перестановка ′, что ′ = , то
′ = ′ = −1 ′ = −1 = −1;
51
если перестановка ′′ такова, что ′′ = , то
−1 = −1 = ′′ −1 = ′′ = ′′.
Таким образом, мы доказали, что множество перестановок с операцией произведения перестановок образуют группу. Эту группу называют группой перестановок или симметрической группой.
Замечание 27.3 . Произведение перестановок в общем случае не коммутативно.
Пример 27.4 . Пусть
1 = ( |
2 |
1 |
3 ) |
, |
2 = ( |
3 |
1 |
2 ). |
|
1 |
2 |
3 |
|
|
1 |
2 |
3 |
Тогда |
( |
1 |
3 |
2 ) |
̸= ( |
3 |
2 |
1 ) |
= 1 2. |
2 1 = |
|||||||||
|
|
1 |
2 |
3 |
|
1 |
2 |
3 |
|
52

Лекция 7. Циклы перестановки, тип перестановки
§28. Циклы перестановки
Будем обозначать
= · · · ; |
0 = ; |
− = −1 −1 · · · −1 .
Определение 28.1 . Циклом длины называется такая перестановка , которая тождественна на всём множестве {1, 2, ..., }, кроме подмножества { 1, ..., }.
Кроме того, ( ) = 1 и ( ) = +1, = 1, − 1. Цикл обычно обозначается
( 1, 2, ..., ) = ( 1, ( 1), ..., −1( 1)).
Определение 28.2 . |
|
Транспозиция |
|
|
- |
перестановка |
элементов |
множества |
||||||||||||||||
{1, 2, ..., }, которая меняет местами только два элемента. |
|
|
|
|
|
|
|
|||||||||||||||||
Замечание 28.3 . Транспозиция — цикл длины 2. |
|
|
|
|
|
|
|
|
|
|||||||||||||||
Утверждение |
28.4 . |
Пусть |
|
и |
{1, ..., }. |
Тогда существует такое |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
число N, что |
|
( ) = . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Доказательство. |
|
|
Пусть |
|
|
{1, ..., }. |
|
Предположим от |
противного, |
|||||||||||||||
что для любого |
|
|
N |
верно |
|
) |
|
= . |
|
Так |
как |
|
множество |
{ |
1, ..., |
} |
||||||||
|
|
|
|
|
|
|
( |
|
2 |
|
̸ |
|
|
|
|
|
|
|
|
|
||||
конечно, а последовательность , ( ), |
|
( ), ..., |
|
( ), ... бесконечна, элементы этой |
||||||||||||||||||||
последовательности будут повторяться. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( ) |
|
|
|
|
|
|
|
Пусть ≥ 0 такое наименьшее целое число, что элемент |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
встретиться в нашей |
|||||
последовательности больше одного раза. То есть существует |
|
> : ( ) = ( ). |
||||||||||||||||||||||
Согласно нашему предположению, ( ) ̸= и, следовательно, |
> 0. |
|
|
|
|
|
||||||||||||||||||
Поскольку |
> 0 |
для элементов ( ) |
и ( ) в последовательности степеней |
|||||||||||||||||||||
перестановки |
от |
существуют предыдущие элементы. Тогда можно записать |
||||||||||||||||||||||
( −1( )) = ( −1( )). |
Из инъективности перестановки следует, что |
−1( ) |
= |
|||||||||||||||||||||
−1( ). Последнее равенство противоречит выбору как степени наименьшего из повторяющихся элементов последовательности, поскольку элемент −1 тоже должен
повториться. Противоречие доказывает утверждение.
Для произвольной перестановки |
|
введем бинарное отношение на |
|
множестве {1, 2, ..., }: |
|
|
|
, {1, ..., } : |
|
|
Z : = ( ). |
Покажем, что — отношение эквивалентности.
53

1) Рефлексивность. Для любого {1, ..., } = 0( ) .
2)Симметричность. Для любых , {1, ..., }, для которых , существует
Z: = ( ). Следовательно, = − ( ) и .
3)Транзитивность. Пусть , , {1, 2, ..., }, и . Тогда существуют1, 2 Z: = 1 ( ), = 2 ( ). Следовательно,
= 2 ( 1 ( )) = 1+ 2 ( ).
То есть .
Пусть {1, 2, ..., } = 1 2 ... — разбиение {1, 2, ..., } на классы эквивалентности относительно . называются орбитами перестановки.
Утверждение 28.5 . Пусть , 1 2 ... — разбиение множества {1, 2, ..., } на классы эквивалентности, порожденное отношением , и ,
= 1, . Тогда
1)для любого {1, 2, ..., } существует N:
= { , ( ), ..., −1( )}.
2) перестановка представима в виде произведения циклов:
= ( 1, ( 1), ..., 1−1( 1)) ( 2, ( 2), ..., 2−1( 2))
· · · ( , ( ), ..., −1( )).
Доказательство. |
1) По определению, |
|
состоит из всех таких , для которых |
|||||||||||||||
существует Z: |
= ( ). |
По утверждению 28.4, для существует |
N: |
|||||||||||||||
( ) = . Пусть |
— наименьшее из таких чисел. Тогда , ( ), ..., −1( ) — |
|||||||||||||||||
различные элементы из {1, 2, ..., } и { , ( ), ..., −1( )} . |
Z |
|
||||||||||||||||
Пусть |
|
|
|
{ |
|
, ( |
), ..., −1( |
) |
} |
. |
Тогда существует такое |
, что |
||||||
|
( ) и |
|
|
|
|
|
|
|
|
|
|
|
||||||
= |
/ |
{1, 2, ..., − 1}. |
= · + , |
Z {0}, {0, 1, ..., − 1}. |
||||||||||||||
Следовательно,
= ( ) = ( · ( )).
Если > 0, то
· ( ) = · · · ( ) = . |
(*) |
Пусть теперь < 0. Тогда, используя равенство (*), получим
· ( ) = − − · · · − ( ) =
−
= − − · · · − ( · · · ( )) = ,
− −
поскольку
− ( ) = −1 |
−1 ... −1 |
|||||
|
|
|
|
|
|
|
... ( ) = .
54

Таким образом, = ( ), где {0, 1, ..., − 1}, что противоречит выбору .
Следовательно, = { , ( ), ..., −1( )}. |
|
|
|
|
|
|
( , ( ), ..., 1−1( )) |
|||||||||
2) Согласно пункту 1 доказательства, для цикла |
|
|
||||||||||||||
выполняется формула |
|
|
{ |
|
. |
|
|
|||||||||
|
|
|
|
|
|
( ), |
|
|
||||||||
|
|
|
( , ( ), ..., 1−1( ))( ) = |
, |
/ |
, |
|
|
||||||||
Обозначим |
|
= ( |
, ( |
), ..., 1−1( |
|
|
|
|
|
|
|
и = , то |
( ) = . |
|||
|
)), = 1, . Если |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
̸ |
|
|
|||
То же верно и для ( ), поскольку ( ) . |
|
|
|
|
|
|
|
|
|
|||||||
Пусть {1, 2, ..., } — произвольное значение. |
Пусть, не умаляя общности, |
|||||||||||||||
. Тогда, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1 2 · · · · · · −1 )( ) =
=( 1 2 · · · · · · −1)( ( )) =
=( 1 2 · · · · · · −1)( ) = · · · =
=( 1 2 · · · )( ) = ( 1 2 · · · −1)( ( )) =
=( 1 2 · · · −1)( ( )) = · · · = 1( ( )) = ( ).
Это верно для любого {1, 2, ..., }. Таким образом,
= ( 1 2 · · · ),
что и требовалось доказать.
Сопоставим каждой орбите перестановку :
{ |
( ), |
. |
( ) = |
, |
/ , |
Будем называть циклы , = 1, , циклами перестановки .
Замечание 28.6 . Из утверждения 28.5 следует, что перестановку можно представить в виде произведения всех ее циклов:
= 1 2 · · · .
Поскольку орбиты не пересекаются, перестановки в этой композиции можно располагать в любом порядке:
= 1 2 · · · ,
где 1 2... — произвольная перестановка из .
55
Пример 28.7 . Пусть = 7 и
= ( |
4 |
2 |
7 |
1 |
3 |
6 |
5 ). |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Найдем орбиты .
(1) |
= 4, 2(1) |
= (4) |
= 1 |
1 |
= {1, 4}, |
(2) |
= 2, |
|
|
2 |
= {2}, |
(3) |
= 7, 2(3) |
= (7) |
= 5, 3(3) = (5) = 3 |
3 |
= {3, 5, 7}, |
(6) |
= 6, |
|
|
4 |
= {6}. |
Представление перестановки в виде произведения циклов |
имеет вид = |
|||||||||
(1, 4)(2)(3, 7, 5)(6). |
|
|
|
|
|
|
|
|
|
|
Пример 28.8 . Пусть = 7 и |
|
|
|
|
|
|
3 ). |
|
|
|
= |
( |
4 |
2 |
5 |
1 |
6 7 |
|
|
||
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
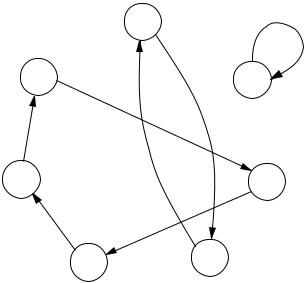
Рассмотрим иллюстрацию к |
утверждению |
28.5 (рисунок 8). |
Обозначим |
|||||||
|
|
|
|
1 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
2 |
|
|
6 |
|
|
3 |
5 |
|
4 |
|
Рисунок 8: Разбиение перестановки на циклы |
|||
каждый элемент множества {1, 2, ..., } вершиной |
графа. Будем рисовать |
||
дугу из вершины в вершину |
, если ( ) |
= . |
Поскольку перестановка |
является биективной функцией, |
из каждой вершины выходит ровно одна дуга |
||
56

и в каждую вершину входит тоже ровно одна дуга. Таким образом, все множество дуг графа разбивается на непересекающиеся контуры: ((1, 4), (4, 1)),
((2, 2)), ((3, 5), (5, 6), (6, 7), (7, 3)). Каждому такому контуру соответствует цикл перестановки .
Определение 28.9 . N — степень перестановки , если — наименьшее из таких натуральных чисел, что = .
Утверждение 28.10 . Пусть , = 1 2 · · · — разложение
на непересекающиеся циклы; — длина цикла . Степень перестановки определяется как наименьшее общее кратное длин ее циклов:
Степень = НОК( 1, 2, ..., ).
Доказательство. Пусть число N таково, что = . Тогда 1 2 · · · = .
Поскольку все перестановки воздействуют на разные элементы {1, 2, ..., }, то= , = 1, . Следовательно, является общим кратным для 1, 2, ..., .
Сдругой стороны, пусть = НОК( 1, 2, ..., ). Тогда = · = , = 1, , и
= 1 2 · · · = .
Пример 28.11 . Степень перестановки из примера 28.7 равна 6.
§29. Тип перестановки
Определение 29.1 . Пусть = ( ) — число циклов длины перестановки .
Тогда ( 1, 2, ..., ) — тип перестановки . Обозначим
( 1, 2, ..., ) = { | , ( 1, 2, ..., ) — тип }.
Замечание 29.2 . ( ) = 1( ) + · · · + ( ) — число циклов перестановки и
|
|
|
∑ |
= |
· ( ). |
|
=1 |
Пример 29.3 . Тип перестановки из примера 28.7 — (2, 1, 1, 0, 0, 0, 0). |
Тип |
||
перестановки из примера 28.8 — (1, 1, 0, 1, 0, 0, 0). |
|
||
Утверждение 29.4 . |
|
||
| ( 1, 2, ..., )| = |
! |
(18) |
|
|
|
||
1! 2! · · · !1 1 2 2 · · · |
|||
57

По утверждению 23.5, множество {1, ..., } можно разбить среди которых ровно подмножеств имеют мощность ,
способами. Чтобы получить перестановку из любого неупорядоченного разбиения, нужно расставить элементы каждого подмножества в определенном порядке, чтобы определить циклы.
Сколько циклов можно получить из одного подмножества мощности ? Элементы
множества можно расставить в различном порядке ! способами. Это число надо разделить на количество вариантов выбора начальный точки цикла — . Таким образом, из данного подмножества можно составить !
различных циклов. Домножим число неупорядоченных разбиений на число вариантов создания циклов
из подмножеств. Получим:
! |
· |
(1!) 1 (2!) 2 · · · ( !) |
= |
|
|
1! 2! · · · !(1!) 1 (2!) 2 · · · ( !) |
1 1 2 2 · · · |
|
! |
|
|
|
|
|
= |
, |
|
|
|
|
|
||
|
|
|
1! 2! · · · !1 1 2 2 · · · |
что и требовалось доказать.
Замечание 29.5 . Утверждение 29.4 может быть доказано и напрямую, если посчитать, сколькими способами можно получить перестановку типа ( 1, 2, ..., ) из перестановок в ,
различным образом расставляя скобки. |
|
|
|
|
|
|
|
|
||
Чтобы узнать это число, |
рассмотрим |
произвольную |
перестановку |
( 1, 2, ..., ) |
||||||
представленную в виде произведения циклов: |
|
|
|
|
|
|
|
|||
(1) |
|
(1) |
(2) |
|
(2) |
(3) |
|
( ) |
, |
( ) |
= 1 |
... 1 |
1 |
... 2 |
1 |
... |
|||||
где ( ) — -тый цикл нашей перестановки длины . Как мы замечали раньше, поскольку циклы перестановки воздействуют на разные элементы, перестановки в этом произведении можно расставлять в произвольном порядке. Сколькими способами мы можем переставить циклы таким образом, чтобы сначала в записи шли все циклы длины 1, затем все циклы длины 2 и т.д.? Очевидно, 1! · 2! · ... · ! способами.
Теперь посчитаем, сколькими способами можно переставить элементы в скобках, обозначающих циклы. Если ( ) в нашей записи обозначает цикл ( 1 , ..., ), то ясно, что первый
элемент в последовательности можно выбрать способами и, значит, у нас есть способов
расставить числа 1 , ..., в скобках, чтобы запись означала один и тот же цикл. Таким образом, для всех циклов перестановки у нас есть 1 1 ·2 2 ·...· способов переставить элементы
в циклах, чтобы запись означала все ту же исходную перестановку .
Рассмотрим следующее отображение . |
Любой перестановке |
типа |
( 1, 2, ..., ) |
|
сопоставим все перестановки (как мы подсчитали, их будет 1! 2! · · · !1 1 2 2 |
· · · ) которые |
|||
получаются, если произвольным образом перемешивать в произведении |
( ) циклы одинаковой |
|||
длины, а для каждого цикла переставлять его элементы в записи по кругу. |
Оказывается, |
|||
образы для разных перестановок типа ( 1, 2, ..., ) не пересекаются (отображение инъективно) и каждая перестановка из входит в образ одной из перестановок типа ( 1, 2, ..., ) (отображение сюръективно).
Значит мы построили взаимно-однозначное соответствие между множеством перестановок типа ( 1, 2, ..., ) и разбиением множества перестановок на группы
58
по 1! 2! · · · !1 1 2 2 · · · штук. |
Поделив мощность |
|
на количество перестановок, |
||
сопоставленных каждой перестановке типа ( 1, 2, ..., ), получим формулу (18). |
|||||
Пример 29.6 . Пусть задан тип перестановки |
(0, 2, 1, 0, 0, 0, 0). Согласно утверждению 29.4, |
||||
число перестановок такого типа должно быть |
|
7! |
7! |
||
|
|
|
= 24 = 7 · 6 · 5 = 210, |
||
|
|
0!2!1!0!0!0!0!10223140506070 |
|||
где 24 — число перестановок, из которых можно получить одну и ту же перестановку типа
(0, 2, 1, 0, 0, 0, 0).
Рассмотрим, например, перестановку (1, 2)(3, 4)(5, 6, 7). Из каких перестановок она может быть получена добавлением скобок? Перечислим такие перестановки:
1)(1, 2, 3, 4, 5, 6, 7), 13) (3, 4, 1, 2, 5, 6, 7),
2)(2, 1, 3, 4, 5, 6, 7), 14) (3, 4, 2, 1, 5, 6, 7),
3)(1, 2, 4, 3, 5, 6, 7), 15) (4, 3, 1, 2, 5, 6, 7),
4)(2, 1, 4, 3, 5, 6, 7), 16) (4, 3, 2, 1, 5, 6, 7),
5)(1, 2, 3, 4, 6, 7, 5), 17) (3, 4, 1, 2, 6, 7, 5),
6)(2, 1, 3, 4, 6, 7, 5), 18) (3, 4, 2, 1, 6, 7, 5),
7)(1, 2, 4, 3, 6, 7, 5), 19) (4, 3, 1, 2, 6, 7, 5),
8)(2, 1, 4, 3, 6, 7, 5), 20) (4, 3, 2, 1, 6, 7, 5),
9)(1, 2, 3, 4, 7, 5, 6), 21) (3, 4, 1, 2, 7, 5, 6),
10)(2, 1, 3, 4, 7, 5, 6), 22) (3, 4, 2, 1, 7, 5, 6),
11)(1, 2, 4, 3, 7, 5, 6), 23) (4, 3, 1, 2, 7, 5, 6),
12)(2, 1, 4, 3, 7, 5, 6), 24) (4, 3, 2, 1, 7, 5, 6).
59
Лекция 8. Принцип включения-исключения, задача о беспорядках
§30. Принцип включения-исключения
Пусть — заданное множество и — множество свойств (множество, элементы которого будут называться свойствами). Каждый элемент из может обладать некоторыми свойствами из . Другими словами, задана функция, сопоставляющая каждому элементу из некоторое подмножество множества :
: → 2 .
Будем говорить, что элемент обладает свойствами ( ). Пусть . Обозначим
=( ) — число элементов из множества , которые обладают всеми свойствами
из и не обладают свойствами из множества |
; |
|
=( ) = |{ : , |
= ( )}| . |
|
≥( ) — число элементов из , которые обладают всеми свойствами из |
и, |
|
возможно, какими-то еще. |
|
|
≥( ) = |{ : , |
( )}| . |
|
Тогда очевидно, что |
|
|
∑ |
|
|
≥( ) = |
=( ). |
(19) |
Далее нам бы хотелось найти обратное соотношение. То есть способ находить значение функции =, зная значения функции ≥.
Утверждение 30.1 . Пусть : 2 → R — произвольная функция, сопоставляющая каждому подмножеству конечного множества некоторое вещественное число. Пусть — такая функция из 2 в R, что
|
∑ |
. |
( ) = |
( ), |
|
|
|
|
Тогда |
∑ |
|
|
( ) = |
(−1)| | ( ), |
. |
|
|
|
|
|
Доказательство. Пусть . Тогда |
∑ |
|
|
∑ |
∑ |
|
|
(−1)| | ( ) = |
(−1)| | |
|
( ) = |
|
|
|
|
60
