
Лекции Просолупов
.pdfэквивалентности совпадает с одним из указанных. Таким образом, отношение сравнимости по модулю порождает различных классов эквивалентности:
[0], [1], ..., [ − 1].
Утверждение 12.5 . Пусть — отношение эквивалентности на множестве . Тогда 1) для любого верно, что [ ]; 2) для любых , , если , то [ ] = [ ] (класс эквивалентности порождается любым своим элементом).
Доказательство. Доказательство пункта 1) следует из рефлексивности отношения
.
Докажем 2). Пусть [ ]. По определению класса эквивалентности . Тогда из и в силу транзитивности отношения следует и [ ]. Следовательно, [ ] [ ].
В силу симметричности отношения верно и . Значит, рассуждая аналогично[ ] [ ]. Таким образом, получим [ ] [ ], что и требовалось
доказать.
Определение 12.6 . Разбиением множества называется совокупность его
попарно непересекающихся непустых подмножеств таких, что каждый элемент принадлежит одному из этих подмножеств:
|
|
|
|
|
|
|
{ 1 2 ... }, |
̸= ?, = 1, , |
|||||
∩ = ?, |
|
|
|
|||
, = 1, , ̸= , |
||||||
= 1 2 ... .
Утверждение 12.7 . Всякое разбиение множества определяет на
отношение эквивалентности : тогда и только тогда, когда и принадлежат одному подмножеству разбиения.
Доказательство. Рефлексивность и симметричность очевидны. Покажем транзитивность. Пусть и . Тогда , 1 и , 2, где 1 и 2 — подмножества разбиения . Поскольку 1 и 2, а подмножества разбиения не могут пересекаться, то 1 = 2. Таким образом, , 1 и .
Утверждение 12.8 . Всякое отношение эквивалентности определяет разбиение множества на классы эквивалентности по этому отношению.
Доказательство. Покажем, что набор классов эквивалентности по отношениюобразуют разбиение . Из утверждения 12.5 следует, что каждый элемент
множества принадлежит некоторому классу эквивалентности. Следовательно, объединение классов эквивалентности равно . В то же время, из того же
21
утверждения следует, что любые два класса эквивалентности либо не пересекаются, либо совпадают, если имеют хоть один общий элемент: [ ], [ ] ,
[ ] = [ ].
Совокупность классов эквивалентности элементов множества по отношению эквивалентности называется фактор-множеством множества по отношению и обозначается /
22
Лекция 3. Отношения порядка
§13. Отношение порядка
Определение 13.1 . Бинарное отношение на множестве называется
отношением порядка, если оно транзитивно и антисимметрично. Множество, на котором введено отношение порядка, называют упорядоченным.
Пример 13.2 . Множество всех пар ( , ) людей, для которых старше , является отношением порядка.
Определение 13.3 . Отношение порядка называется отношением нестрогого
(частичного) порядка на множестве X, если оно рефлексивно.
Отношение порядка называется отношением строгого порядка на множестве X, если оно иррефлексивно.
Определение 13.4 . Отношение порядка на множестве называется отношением линейного порядка, если любые , , ̸= , сравнимы в смысле отношения (либо , либо обязательно выполняется).
Пример 13.5 . 1) Отношение родитель-ребенок (рисунок 3-a)) не является отношением порядка. Очевидно, что у такого отношения отсутствует транзитивность: дед не является родителем своего внука.
С другой стороны, отношение предок-потомок является отношением порядка. На рисунке 3-b) представлено то же фамильное дерево, что и на рисунке 3-a), но с указанием всех связей от дедов к внукам.
Отношение предок-потомок является отношением строгого порядка и не является линейным порядком.
2) > = {( , ) | , R, > } — является отношением строгого линейного порядка.
3) ≥ = {( , ) | , R, ≥ } — является отношением нестрогого линейного порядка.
4) Отношение , состоящее из всех таких пар подмножеств ( , ) заданного
универсального множества , что является подмножеством множества ,
называют отношением включения. Отношение включения является отношением нестрогого порядка и не является отношением линейного порядка.
Определение 13.6 . Пусть на множестве введено отношение порядка. Пусть элемент таков, что не существует такого , ̸= , что . Тогданазывают минимальным элементом.
Определение 13.7 . Пусть на множестве введено отношение порядка. Пусть элемент таков, что для любых , ̸= , выполняется . Тогда называют наименьшим элементом.
23
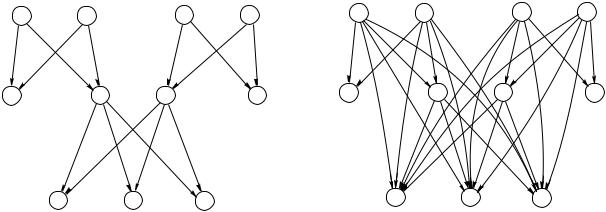
a) |
b) |
Рисунок 3: Генеалогическое древо
Замечание 13.8 . Может существовать несколько минимальных элементов и только один наименьший.
Аналогично определениям 13.6 и 13.7 можно определить максимальный и наибольший элементы.
Лемма 13.9 . Если на конечном непустом множестве задан линейный порядок, то существует наименьший элемент, и он единственен.
Доказательство. Для нахождения наименьшего элемента выберем произвольный элемент из и будем сравнивать его поочередно с остальными элементами из .
В силу линейности порядка, любой элемент из сравним с . Если найдется какойнибудь элемент , для которого , то по свойству транзитивности окажется, что предшествует всем уже просмотренным нами ранее элементам множества(то есть является для всех просмотренных наименьшим). Продолжим перебор элементов, сравнивая теперь оставшиеся элементы из с элементом , пока не найдем такой , что . И т.д. Будем повторять процесс, пока не переберем все элементы из . Элемент, выбранный для сравнения с остальными на тот момент и будет наименьшим элементом множества .
Единственность следует из определения наименьшего элемента и антисимметричности отношения порядка. Действительно, если бы существовало два наименьших элемента и ( ̸= ), то по определению наименьшего элемента
и . Из этого по свойству антисимметричности отношения порядка следовало бы = .
Теорема 13.10 . Пусть на конечном непустом множестве задан линейный
24
порядок. Тогда на можно выбрать такую нумерацию элементов 1, 2, ..., ( = { 1, 2, ..., }), что соотношение ( и ̸= ) будет выполняться в том и только в том случае, когда < .
Доказательство. Согласно лемме 13.9, для множества существует наименьший элемент, то есть такой 1 , что 1 для любых . Удалим элемент 1 из множества .
Множество { 1} также удовлетворяет условиям леммы 13.9 и, значит, в нем тоже существует наименьший элемент — 2.
Мы можем повторять этот процесс до тех пор, пока в множестве не закончатся
элементы. По способу выбора элементов очевидно, что 1, 2, ..., и есть искомая нумерация.
Определение 13.11 . |
Два нестрого упорядоченных |
множества |
и |
|
||||
называются изоморфными, если существует биекция |
: |
→ , сохраняющая |
||||||
отношение нестрогого |
порядка. |
Иными словами, |
если |
и отношения |
||||
нестрогого порядка соответственно множеств и , то |
|
|
|
|||||
|
|
1 2 |
( 1) ( 2). |
|
|
|
||
Пример 13.12 . |
Рассмотрим множество |
2 всех подмножеств множества |
||||||
= {1, 2, 3}, |
упорядоченное |
отношением |
включения, |
и множество |
|
= |
||
{1, 2, 3, 5, 6, 10, 15, 30}, упорядоченное отношением |
|
|
|
|
||||
делится на .
Эти два упорядоченных множества схематично изображены на рисунке 4. Точки соответствуют элементам множеств 2 (на рисунке a)) и (на рисунке
b)). Линия снизу вверх соответствует непосредственному отношению между двумя элементами. Остальные линии не отображены, чтобы не загромождать
изображение. Например, линия между ? и {2, 3} на рисунке a) не нарисована, но
отношение между этими элементами предполагается в силу транзитивности. Из рисунка хорошо видно, что эти два упорядоченных множества изоморфны.
Теорема 13.13 . Всякое нестрого упорядоченное множество изоморфно
некоторой системе подмножеств множества , нестрого упорядоченной отношением включения.
Доказательство. Пусть — отношение нестрогого порядка на множестве . Для каждого элемента рассмотрим множество = { | }. Ясно, что для любого . Покажем, что система подмножеств { |}, упорядоченная отношением включения, есть искомая система подмножеств.
Рассмотрим отображение
: → { | }
25

{1,2,3}
{2,3} |
{1,3} |
{1,2} |
{3} |
{2} |
{1} |
a)
30 |
15 |
10 |
|
6 |
5 |
3 |
2 |
1 |
b)
Рисунок 4: Изоморфные нестрого упорядоченные множества
такое, что ( ) = . Если = , то, поскольку , то и, следовательно,. Аналогично, . Таким образом, в силу антисимметричности отношения ,
= . Значит, отображение инъективно. С другой стороны, у любого множества
есть прообраз . Значит, сюръективно. Следовательно, — биекция.
Пусть . Тогда из в силу транзитивности отношения следует , а значит . Пусть . Тогда, поскольку , то и, следовательно,. Таким образом, биекция сохраняет отношение нестрогого порядка.
§14. Лексикографический порядок
Заслуживающим отдельного упоминания является лексикографический порядок. Лексикографический порядок - это порядок, в котором выстроены слова, например, в орфографических и русско-английских словарях.
Лексикографический порядок может быть введен на множестве слов (упорядоченных последовательностей элементов) над любым множеством, на котором уже введен строгий линейный порядок.
Пусть на множестве введен строгий линейный порядок . Введем отношение
на множестве * = {( 1, 2, ..., ) | N, } всех слов над множеством
. Пусть ̃ = ( 1, ..., ) *, ̃ = ( 1, ..., ) *, ̃ ̸= ̃ и ≤ .
Будем говорить, что ̃ ̃ , если 1) существует такой индекс , 1 ≤ ≤ , что
= , = 1, − 1 и , или 2) < и = , = 1, . В противном случае
̃ ̃ .
Замечание 14.1 . На множестве слов одинаковой длины определение
26

лексикографического порядка упростилось бы и приняло бы вид:
Пример |
|
|
|
{1, ..., } : = , = |
1, − 1 |
, . |
|
̃ |
̃ |
|
|
|
|
|
|
|
14.2 . Выпишем все возможные перестановки чисел {1, 2, 3, 4}, |
||||||
выстроенные в лексикографическом порядке: |
|
|
|
||||
|
|
1 2 3 4 |
|
2 1 3 4 |
3 1 2 4 |
4 1 2 3 |
|
|
|
1 2 4 3 |
|
2 1 4 3 |
3 1 4 2 |
4 1 3 2 |
|
|
|
1 3 2 4 |
|
2 3 1 4 |
3 2 1 4 |
4 2 1 3 |
|
|
|
1 3 4 2 |
|
2 3 4 1 |
3 2 4 1 |
4 2 3 1 |
|
|
|
1 4 2 3 |
|
2 4 1 3 |
3 4 1 2 |
4 3 1 2 |
|
|
|
1 4 3 2 |
|
2 4 3 1 |
3 4 2 1 |
4 3 2 1 |
|
Заметим, что здесь мы привели только перестановки — последовательности из различных символов. Если мы захотим выписать все слова в данном алфавите, их окажется гораздо больше.
Отметим также, что существует еще так называемый антилексикографический порядок. Он не является обратным лексикографическому порядку бинарным отношением. Список всех перестановок чисел в антилексикографическом порядке
может быть получен следующим образом: сначала нужно выстроить все такие перестановки в лексикографическом порядке, а затем развернуть список в обратном порядке и развернуть каждое слово, описывающее перестановку. Такой порядок может быть полезен, например, для словаря окончаний.
Используя те же обозначения и договоренности, что и при введении лексикографического порядка, антилексикографический порядок можно определить следующим образом:
Будем говорить, что ̃ ̃ , если 1) существует такой индекс , 1 ≤ ≤ , что
− +1 = − +1, = 1, − 1 и − +1 − +1, или 2) < и − +1 = − +1, = 1, . В
противном случае ̃ ̃ .
Замечание 14.3 . На множестве слов одинаковой длины определение приняло бы следующий вид:
|
|
|
|
|
|
|
{1, ..., } : = , = + 1, , |
. |
|||||
̃ |
̃ |
|||||
Пример 14.4 . Приведем все возможные перестановки чисел {1, 2, 3, 4}, выстроенные в антилексикографическом порядке:
1 2 3 4 |
1 2 4 3 |
1 3 4 2 |
2 3 4 1 |
2 1 3 4 |
2 1 4 3 |
3 1 4 2 |
3 2 4 1 |
1 3 2 4 |
1 4 2 3 |
1 4 3 2 |
2 4 3 1 |
3 1 2 4 |
4 1 2 3 |
4 1 3 2 |
4 2 3 1 |
2 3 1 4 |
2 4 1 3 |
3 4 1 2 |
3 4 2 1 |
3 2 1 4 |
4 2 1 3 |
4 3 1 2 |
4 3 2 1 |
Лексикографический и антилексикографический порядки являются отношениями строгого линейного порядка.
27
Лекция 4. Размещения и сочетания, бином Ньютона, формула обращения
§15. Размещения и сочетания |
|
|
Пусть имеется множество = { 1, 2, ..., }. |
Набор элементов 1 , 2 , ..., |
|
из множества называется выборкой объема |
|
( -элементной выборкой) из |
элементов.
Выборка называется упорядоченной, если порядок элементов в ней задан. Иначе выборка называется неупорядоченной.
Также различают выборки с повторениями и без повторений в зависимости от того, допускается или не допускается повторное вхождение в выборку одних и тех же элементов.
Пример 15.1 . Пусть = {1, 2, 3}. Тогда (1, 1), (1, 2), (1, 3), (2, 1), (2, 2), (2, 3),
(3, 1), (3, 2), (3, 3) — все возможные упорядоченные выборки объема два из трех элементов.
Определение 15.2 . Размещением из элементов по называется упорядоченная выборка без повторений объема из -элементного множества.
Поскольку элементы нашего множества пронумерованы некоторым образом, не умаляя общности, можно называть размещением из элементов по упорядоченный набор из различных чисел, принадлежащих множеству {1, ..., }.
Обозначим количество различных размещений из по .
Пример 15.3 . 1) Пусть на экзамене у преподавателя различных билетов и
сдавать пришло студентов. Тогда существует ровно способов выдать всем
студентам по одному билету для подготовки.
2) Пусть = {1, 2, 3}. Тогда (1, 2), (1, 3), (2, 1), (2, 3), (3, 1), (3, 2) — все возможные размещения из трех элементов по два.
Утверждение 15.4 . Пусть , N и 1 ≤ ≤ . Тогда
= · ( − 1) · ... · ( − + 1) = |
|
! |
|
. |
|
|
|
||
( |
− |
)! |
||
|
|
|
|
Доказательство. Действительно, существует различных способов выбрать первый элемент набора из элементов множества {1, ..., }. Аналогично, существует− 1 способ выбора второго элемента и так далее.
Определение 15.5 . Сочетанием из элементов по называется неупорядоченная выборка без повторений объема из -элементного множества.
28
Как и раньше, |
можем считать, что |
|
сочетанием из элементов по |
||||||
называется неупорядоченный набор из |
|
|
различных |
чисел, |
принадлежащих |
||||
множеству {1, ..., }. |
|
|
|
|
|
|
|
|
|
Количество сочетаний из по обозначим или . |
|
|
|
||||||
|
|
|
из |
|
|
( ) |
|
|
|
Пример 15.6 . |
1) |
Предположим, |
|
|
участников |
спортивного |
клуба на |
||
соревнования должны |
поехать какие-то |
. |
Тогда имеется |
|
различных |
||||
|
|
|
|
|
|
|
|
|
|
возможности собрать команду.
2) Пусть = {1, 2, 3}. Тогда {1, 2}, {1, 3}, {2, 3} — все возможные cочетания из трех элементов по два.
Определение 15.7 . Множество всех подмножеств множества мощности
будем обозначать |
( |
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
( |
|
= |
{ |
|
| |
|
|
, |
| |
|
| |
= |
} |
. |
|
|
|
|
) |
|
|
|
|
|
|
|
|||||||
Пример 15.8 . |
Пусть = {1, 2, 3, 4, 5} и |
= 3. |
Тогда = { {1, 2, 3}, {1, 2, 4}, |
||||||||||||||
( )
{1, 2, 5}, {1, 3, 4}, {1, 3, 5}, {1, 4, 5}, {2, 3, 4}, {2, 3, 5}, {2, 4, 5}, {3, 4, 5} }
Нетрудно видеть, что если мощность множества равна , то
( ) = |
(| |) |
= |
( ). |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Утверждение 15.9 . Пусть , N и 1 ≤ ≤ . Тогда
( ) |
= |
!( ! |
)! |
|
|
|
|
|
|
− |
|
Доказательство. Действительно, каждому сочетанию из
(1)
(2)
по соответствует !
различных размещений из по с различным порядком следования элементов.
|
|
|
|
! |
|
|
|
||
Тогда ( ) |
= |
! |
= |
!( − )! |
Очевидным следствием из формулы (2) является равенство
( ) |
= |
( − ). |
(3) |
|
|
|
|
Интуитивно эту формулу можно было бы обосновать следующим рассуждением. Выбирая элементов из , мы тем самым выбираем − элементов из , которые не
попадают в нашу выборку. Проще говоря, мы разбиваем наше множество мощностина два подмножества мощностей и − соответственно.
Также можно непосредственно подстановкой формулы (2) убедиться в правильности равенства
( ) |
· |
( ) |
= |
( ) |
· |
( |
−− ). |
(4) |
|
|
|
|
|
|
|
|
|
29

Действительно,
( ) |
· |
( ) |
= |
!( |
|
|
)! · |
!( |
|
)! |
· ( |
− )! = |
|||||
|
|
|
|
|
! |
|
|
|
! |
|
|
|
( |
)! |
|||
|
!( − )! · |
|
|
− |
|
|
|
− |
|
|
|
|
− |
||||
|
( − )!( − )! |
|
( ) · ( − ) |
||||||||||||||
= |
|
|
! |
|
|
( |
− )! |
|
= |
|
|
|
− . |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Интуитивно формулу (4) можно описать как разбиение множества из элементов на три подмножества мощностей , − , − соответственно. Левая часть равенства описывает выбор сначала элементов из , а затем элементов из выбранных . Получим все варианты разбиения исходного множества на три
подмножества указанных мощностей.
Правая часть равенства соответствует выбору сначала элементов из , а затем− элементов из оставшихся − . Получим те же варианты подмножеств.
§16. Треугольник Паскаля
Утверждение 16.1 . Пусть , N и 2 ≤ ≤ . Тогда
( ) |
( − 1) |
( |
|
) |
|
|
= − 1 |
+ |
− 1 |
. |
(5) |
Это равенство довольно легко доказать, явно подставив выражение согласно формуле (2), но приведем другое доказательство этого факта.
Доказательство. Пусть множество имеет вид: = { 1, 2, ..., }. Определим множества и следующим образом:
= {{ 1 , 2 , ..., −1 , } | { 1 , 1 , ..., −1 } |
( |
{ |
1 |
}) } |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
|
|
|
|
) |
|
|
|
|
|
− |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
{ } |
|
|
|
|
|
|
|
|
|
||
Очевидно, ∩ = ?. Кроме того, можно видеть, что |
|
|
= , поскольку все - |
||||||||||||||||||||||||
элементные сочетания из |
|
, содержащие |
|
, находятся в , а все такие -элементные |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
) |
| |
= | | + | |. Учитывая, |
||||||
сочетания, которые не содержат , лежат |
в . Тогда | |
||||||||||||||||||||||||||
что по формуле (1) |
|
|
= |
|
|
|
, |
= |
|
−1 |
|
и |
= |
−1 |
|
, |
получаем искомое равенство |
||||||||||
|
|
)| |
|
|
( |
|
) |
| | |
|
( |
|
|
1 |
) |
|
|
| | |
( |
|
|
( |
) |
|
|
|
||
(5). |
|( |
|
|
|
|
|
− |
|
|
|
|
) |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Положим следующие естественные начальные условия для числа сочетаний из
по : 00 |
= 1; |
0 |
= 1 для любых N; |
|
= 0 для любых > . Тогда, пользуясь |
( |
) |
( |
) |
( |
) |
рекуррентным соотношением (5), можно построить следующую таблицу, которую называют треугольником Паскаля:
30
