Давыд Цуриков. Диссертация. 2015 г

21

1.2.3. Позиционирование уровня Ферми

Параметры плёнки

Оценим величину поверхностного потенциала, при котором уровень Ферми можно позиционировать относительно системы 2D энергетических уровней носителей заряда. Для этого применим предложенный в подразделах 1.2.1 и 1.2.2 алгоритм к расчёту ОПЗ

Не умаляя общности предложенной вычислительной процедуры, для иллюстрации принципа позиционирования уровня Ферми рассмотрим случай собственного полупроводника.

Результаты расчёта

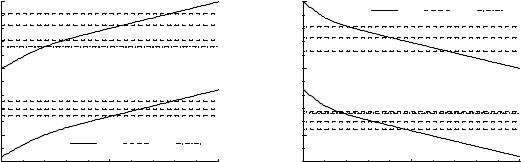
На рисунке 2 изображена энергетическая структура плёнки собственного германия. В обоих случаях уровни энергии разрешены, так как расстояние между ними превосходят значение k0T ≈ 0.026 эВ. При одинаковых по модулю значениях VS уровни двумеризован-

ных электронов разрешены лучше, чем уровни дырок. Это связано с тем, что размерное квантование для электронов более существенно вследствие их меньшей нормальной эф-

фективной массы: m− < m+ . Однако уровень Ферми находится внутри системы уровней только в случае дырок (рис. 2b). Для достижения аналогичного эффекта в случае электронов следует приложить больший поверхностный потенциал. Поэтому при выборе оптимального материала, формирующего полупроводниковую структуру, нельзя однозначно отдать предпочтение полупроводникам с малой нормальной эффективной массой носителей заряда. Несмотря на лучшее разрешение уровней лёгких носителей, они слабее проседают с ростом поверхностного потенциала.

Расчёты для легированных плёнок германия показали, что позиционирование уровня Ферми в энергетической структуре предпочтительнее для основных носителей заряда (состояние обогащения). Для достижения аналогичного эффекта в случае неосновных носителей (состояние инверсии) следует прикладывать существенно большие потенциалы. При двумеризации основных носителей заряда вследствие сильной экранировки потенциал быстро спадает вглубь пленки, и приповерхностная потенциальная яма оказывается узкой.

Это приводит к необходимости дальнейшего увеличения VS . По этой причине нельзя от-

дать предпочтение легированным полупроводникам.

Резюме

Таким образом, уровень Ферми можно позиционировать в системе энергетических уровней двумеризованных носителей заряда в полупроводниковой плёнке. При этом величину поверхностного потенциала можно считать приемлемой. Для расчёта его точного значения следует решать самосогласованную задачу для конкретной планарной системы. Это связано с тем, что наличие латеральной структуры может привести к размерному квантованию в плоскости плёнки. Как видно на примере простых систем (табл. 4), данный эффект повлияет на закон дисперсии и плотность одночастичных состояний, что изменит электростатический потенциал в полупроводниковой плёнке.

23

1.3.Выводы

Вданной главе были сформулированы основные приближения настоящей работы и определения физики низкоразмерных систем. В силу актуальности структур на основе двумерного газа носителей заряда была предложена быстрая схема квантового самосогласованного расчёта ОПЗ полупроводниковой плёнки в случае омического контакта на тыльной стороне. Расчёт основан на совместном решении уравнений Шрёдингера и Пуассона. Повышение его скорости и устойчивости достигается следующим образом:

•расчёт уровня Ферми на основе уравнения электронейтральности без самосогласова-

ния (20);

•при каждом значении поверхностного потенциала VS индивидуальный расчёт для электронов и дырок только тех уровней энергии, которые существенно влияют на заряд в ОПЗ (23);

•выход из самосогласованной процедуры при достижении заданной точности расчёта поверхностной плотности заряда в ОПЗ (26);

•расчёт уровней энергии на основе метода стрельбы для задачи Коши (42) с учётом правила формального смещения границы плёнки (40), с применением алгоритма Верле в скоростной форме (45), (46) на сетке с постоянным шагом;

•локализация уровней энергии на основе параболической экстраполяции (49). Квантовый самосогласованный расчёт ОПЗ был реализован в виде программного кода

на языке C++. В рамках настоящей диссертации программа использовалась применительно к плёнке собственного германия. Это позволило проиллюстрировать принцип позиционирования уровня Ферми в энергетическом спектре носителей заряда посредством верхнего затвора (рис. 1a). Поэтому при проектировании устройств на базе двумерного электронного газа в главе 3 будем полагать, что уровень Ферми можно установить наперёд заданным образом. Чтобы найти электрические токи через такие разветвлённые низкоразмерные структуры, сформулируем в главе 2 объединённую схему расчёта.

24

Глава 2. Электронный транспорт

внизкоразмерных структурах

Вработах, посвящённых квантовому электронному транспорту в низкоразмерных структурах, присутствуют, в известной степени, оригинальные обозначения. Поэтому в обзорном разделе 2.1 изложение будет дано с минимальной формализацией, уточнить которую можно по предоставленным ссылкам. Такой подход позволит избежать возможных конфликтов обозначений, при этом он даст качественное представление о материале. Последовательная формализация рассматриваемой задачи будет проведена в разделе 2.2 (см. также приложение H).

Оригинальный материал данной главы распределён по разделам следующим образом.

1.Система обозначений. В подразделе 2.2.1 предложена система обозначений, позволяющая упростить расчёт электрических токов через низкоразмерные структуры [А3].

2.Граничные условия рассеяния. В подразделе 2.2.3 для расчёта расширенной матрицы рассеяния узла квантовой сети предложены граничные условия рассеяния в интегродифференциальной формулировке [А1].

3.Сетевая формула. В подразделе 2.2.4 предложена формула для расчёта расширенной матрицы рассеяния квантовой сети в терминах расширенных матриц рассеяния её узлов [А3].

4.Электрические токи. В подразделе 2.3.2 для расчёта электрических токов через квантовую сеть предложен формализм Ландауэра–Бюттикера, адаптированный к используемой в работе системе обозначений.

2.1.Моделирование разветвлённых низкоразмерных структур

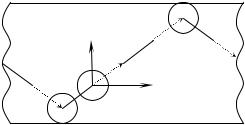
Математической моделью, описывающей электронный транспорт в разветвлённых низкоразмерных структурах, является квантовая сеть (quantum network) [23, 24]. Конструктивно квантовая сеть состоит из квантовых точек, соединённых друг с другом квантовыми проволоками (табл. 3). Поскольку носитель заряда может рассеиваться как в точке, так и на участке проволоки, удобно ввести функциональное определение: квантовая сеть – совокупность рукавов и узлов. Рукав (branch) – элемент сети, в котором носитель заряда не рассеивается. Узел (junction) – элемент сети, в котором носитель заряда рассеивается.

25

2.1.1. Специфика электронного транспорта

Динамика электрона

Не умаляя общности, будем говорить о движении электрона в кантовой сети. Рассмотрим наглядный классический аналог электрона в рукаве: упругий шар в трубе с жёсткими стенками (рис. 3). Пусть шар в трубе движется без вращения с кинетической энергией E :

p

p

Рис. 3. Классический аналог электрона в рукаве квантовой сети:

упругий шар в трубе с жёсткими стенками. p и p – продольная и поперечная составляющие импульса шара соответственно.

Согласно (51) и (52)

где E – кинетическая энергия шара, связанная с его движением вдоль трубы (продольная энергия), E – кинетическая энергия шара, связанная с его движением поперёк трубы от стенки к стенке (поперечная энергия). Попав в участок соединения нескольких труб (узел), шар рассеивается в нём. Вследствие этого он попадает в ту же трубу, либо в одну из прочих. При упругом рассеянии энергия E сохраняется, а E и E могут иметь любые положительные значения в пределах равенства (53). В классической механике этот про-

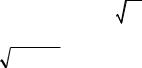
26

цесс однозначно детерминирован: по известным начальным координатам и скорости шара можно предсказать, где и с какой скоростью он будет двигаться.

Рассмотрим движение электрона с энергией E в рукаве. При этом верна формула (53). Специфика рукава состоит в том, что его поперечные размеры сравнимы с длиной волны де Бройля электрона. Это приводит к размерному квантованию его поперечной энергии:

где E n – энергия размерного квантования электрона в рукаве, квантовое число n прини-

Поэтому физический смысл выражения (56) состоит в том, что при фиксированной энергии E электрон может распространяться в рукаве только в дискретном наборе состояний, удовлетворяющих неравенству (57).

Возникшие вследствие размерного квантования уровни энергии {E n}n с ассоцииро-

ванным движением электрона вдоль рукава называются каналами. Каналы, удовлетворяющие неравенству (57), именуют открытыми, не удовлетворяющие – закрытыми. Тип канала определяется значением энергии электрона E и видом поперечного сечения рука-

ва, задающим набор значений {E n}n .

С точки зрения квантовой механики, за движение электрона вдоль рукава отвечают экспоненциальные множители в волновых функциях. Показатель экспонент в открытых каналах является чисто мнимым, в закрытых – вещественным. Поэтому электронные волны в первом случае называют бегущими, во втором – исчезающими.

Электрические токи

Электрон в рукаве может находиться сразу в нескольких каналах с определённой вероятностью. Процесс рассеяния электрона в узле также носит вероятностный характер. В основе расчёта токов в этом случае лежит квантовая теория рассеяния.

Вероятностный характер движения электрона в квантовой сети учитывается в рамках формализма Ландауэра–Бюттикера [25]. Проиллюстрируем его на примере узла с двумя

27

примыкающими к нему многоканальными рукавами, соединёнными с удалёнными резервуарами электронов. В этом случае выражение для тока запишется как [26, с. 1048]

где Tnm – вероятность прохождения электрона между рукавами из открытого канала m в

открытый канал n (прозрачность). Функции распределения электронов в резервуарах имеют вид

где μα – электрохимический потенциал резервуара α , Θα – температура резервуара α в

энергетических единицах.

Прозрачность {Tnm}nm связывает токи в каналах, прошедшие через узел, с входящими в него. Токи в каналах можно найти на основе амплитуд волн электронов. Амплитуды волн, рассеянных узлом, с амплитудами падающих на него связывает матрица рассеяния (S-

матрица). Чтобы записать прозрачности Tnm через квадраты модулей элементов матрицы рассеяния, те предварительно следует умножить на k n / km , где k n = 2m(E − E n ) / –

волновое число канала n [26, с. 1048]. Это связно с видом волновых функций в рукавах и определением для тока в квантовой механике. Полученный таким образом объект называется потоковой матрицей рассеяния [27, 28]. Иногда в литературе S-матрицу вводят так, что она с ней совпадает [26].

Резонансы

Поведение потоковой матрицы рассеяния как функции энергии определяется расположением её комплексных полюсов – резонансных энергий [28]. Их влияние становится особенно существенным, когда они находятся вблизи вещественной оси. В области резонанса (внутри круга радиусом с мнимую часть полюса) элементы потоковой матрицы рассеяния сильно варьируются. Поэтому резонансы проявляются обычно в виде пиков и впадин в прозрачностях, и их можно наблюдать в транспортных свойствах структуры.

Возникновение резонансов связано с открытостью системы. Когда квантовая система сцеплена (запутана) с контактами, она становится открытой, и вещественные энергии связанных состояний закрытой задачи мигрируют в нижнюю полуплоскость комплексной энергии, становясь резонансными энергиями. Характерной особенностью резонансов является то, что в таких состояниях все матричные элементы потоковой матрицы рассеяния

28

сингулярны. Поэтому вблизи них все коэффициенты прохождения между разными каналами имеют сходную зависимость от энергии.

2.1.2. Методы расчёта матрицы рассеяния

Граничные условия рассеяния

S-матрицу узла можно найти путём прямого решения уравнения Шрёдингера в нём. Для этого на его границах следует поставить граничные условия рассеяния (scattering boundary conditions) [29–31]. Они обеспечивают сшивание (совпадение значений функций и их производных) волновой функции в узле с падающими и рассеянными волнами в рукавах. Метод граничных условий рассеяния (ГУР) является универсальным и гибким, что обеспечивает ему широкую область применения.

С помощью ГУР, поставленных для двумерного уравнения Шрёдингера, в работе [29] было исследовано влияние локальных дефектов на электронный транспорт в многоканальных квантовых проволоках при T = 0 K . В качестве узла был рассмотрен участок проволоки, содержащий дефекты. Примыкающие к узлу участки (рукава) предполагались полубесконечными. Это позволило учесть в них только открытые каналы, исключив из рассмотрения исчезающие волны со стороны резервуаров. Дефекты в проволоке проявили себя в флуктуациях её проводимости порядка e2 / h . Проведенные в работе аналитические и численные расчёты являются основой для интерпретации результатов экспериментов.

Трёхмерная задача с применением ГУР для уравнения Шрёдингера была рассмотрена в работе [30]. Предложенный на их основе метод численного расчёта использовался для исследования транспортных свойств нульмерных резонансных туннельных диодов на базе квантовых точек. Полученная таким образом многоканальная S-матрица позволила найти туннельный ток через устройство. Также на основе использованной численной схемы проведено исследование резонансного туннелирования через диод за счёт квазисвязанных состояний, индуцированных ионизованными примесями в квантовой точке.

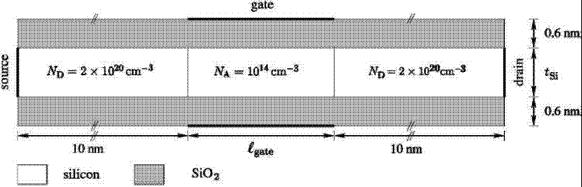
Важной особенностью ГУР является возможность их применения для квантового самосогласованного расчёта тока через всевозможные наноструктуры. Так в работе [31] был проведён расчёт вольт-амперных характеристик ультратонкого двухзатворного МДПтранзистора (рис. 4). Самосогласованные рассеянные волновые функции были вычислены на основе многоканальной S-матрицы. Развитый в работе метод позволил детально изучить влияние геометрии прибора на его транспортные свойства.

29

Рис. 4. Конструкция двухзатворного МДП-транзистора.

Формализм DN- и ND-map

Влитературе, как правило, вид граничных условий рассеяния определяется конкретной задачей, что снижает их наглядность. К недостаткам также можно отнести их «нестандартный» вид. Это затрудняет реализацию метода ГУР во многих вычислительных пакетах. Схемы расчёта S-матрицы на основе граничных условий Дирихле и Неймана являются более удобными для применения. К числу таких схем относится метод Dirichlet-to- Neumann и Neumann-to-Dirichlet отображений (DN- и ND-map).

Следуя обозначениям работы [24], введём определения. DN – Dirichlet-to-Neumann map (DN-map) – оператор, который ставит в соответствие граничным условиями Дирихле граничные условия Неймана: значения нормальной производной функции, являющейся решением задачи Дирихле. ND – Neumann-to-Dirichlet map (ND-map) – оператор, который ставит в соответствие граничным условиями Неймана граничные условия Дирихле: граничные значения функции, являющейся решением задачи Неймана. Эти операторы являются обратными друг другу: DN ND = I , где I – единичная матрица.

Врамках задачи рассеяния электрона в квантовой сети речь идёт о DN- и ND-map на границах узла с рукавами. Записывая операторы этой задачи в виде матриц, в их структуре можно выделить блоки, отвечающие за связь между каналами различного типа. Нижние индексы «+» и «–» будут относиться к открытым и закрытым каналам соответственно. Согласно работам [23, 24], для матрицы рассеяния верны выражения вида

где матрицы M и N определяются посредством соответствующих формул Крейна:

30

K – диагональная матрица волновых чисел каналов.

Согласно формализму работы [24] для S-матрицы узла была получена приближённая формула на основе разрешимой подгоночной модели нулевого радиуса. Был интерпретирован феноменологический параметр в граничных условиях для T-узла. Также предложено использовать данную модель в качестве первого шага в расчёте S-матрицы по модифицированной теории возмущений. Предложенный полуаналитический подход получил развитие в работе [32].

Формализм DN-map также показал свою эффективность в расчётах квантовых моделей полупроводниковых устройств. В работах [33, 34] на его основе был проведён расчёт двумерного переключателя. В них была предложена конструкция переключателя на основе круглого узла с примыкающими к нему четырьмя полубесконечными одноканальными рукавами. Переключение происходило за счёт поворота электрического поля в плоскости прибора. На основе приближённой формулы для матрицы рассеяния выявлены характеристики устройства в зависимости от температуры, уровня Ферми и эффективной массы электрона. Дана оценка скорости переключения.

Формализм R-матрицы

Применительно к расчёту S-матрицы полупроводниковых квантовых структур в литературе также широко распространён формализм R-матрицы [27, 28, 35]. R-матрица выражает значения волновой функции на границах узла с рукавами через её нормальную производную [36]. Её определение идентично определению ND-map. Связь с S-матрицей имеет тот же вид (61) с точностью до обозначений [36]. Поэтому формализм R-матрицы так же эффективен в решении задач рассеяния, как и метод ND-map.

В работе [36] формализм R-матрицы рассмотрен на примере двухполюсной периодической двумерной системы при T = 0 K . Система имела несколько периодов за счёт моду-

лирующего потенциала. Одномерность потенциала позволила упростить расчёты. Была рассчитана многоканальная проводимость системы при различном числе периодов и варьировании их длин.

Полученный ранее результат для одномерного транспорта [36] был обобщён для многополюсных систем [27]. В качестве примера рассчитана проводимость двумерной системы при T = 0 K с потенциалом типа Кронига–Пенни в латеральном направлении. В пре-