
Банк задач, механика , молекулярная физика и термодинамика, 1 семестр
.docx30
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
473 |
Точка
участвует одновременно в двух
гармонических колебаниях, происходящих
по взаимно перпендикулярным направлениям
и описываемых уравнениями х=А1 |
2 |
3 |
1 |
0,5 |
- |
|
474 |
То же |
2 |
3 |
0,5 |
0,5 |
- |
|
475 |
То же |
2 |
2 |
1 |
1 |
- |
|
476 |
То же |
1 |
1 |
1 |
1 |
- |
|
477 |
Материальная
точка участвует одновременно в двух
взаимно перпендикулярных колебаниях,
выражаемых уравнениями х=А1 |
5 |
3 |
- |
- |
- |
|
478 |
То же |
4 |
1 |
- |
- |
- |
|
479 |
То же |
5 |
5 |
- |
- |
- |
|
480 |
То же |
15 |
10 |
- |
- |
- |
|
481 |
Материальная
точка массой m=А кг совершает колебания,
уравнение которых имеет вид: х=А |
0,05 |
0,1 |
5 |
3 |
- |
|
482 |
То же |
0,01 |
0,2 |
10 |
4 |
- |
|
483 |
То же |
0,02 |
0,3 |
20 |
6 |
- |
|
484 |
То же |
0,04 |
0,4 |
15 |
2 |
- |
|
485 |
Колебания
материальной точки происходит согласно
уравнение х=А |
8 |
6 |
5 |
100 |
- |
|
486 |
То же |
10 |
8 |
5 |
50 |
- |
|
487 |
То же |
6 |
4 |
10 |
80 |
- |
|
488 |
То же |
|
|
|
|
|
|
489 |
Груз, массой m=А г, подвешенный к пружине, колеблется по вертикали с периодом Т=В с. Определить жесткость пружины. |
150 |
1,0 |
- |
- |
- |
31
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
490 |
То же |
250 |
1,0 |
- |
- |
- |
|
491 |
То же |
200 |
1,5 |
- |
- |
- |
|
492 |
То же |
300 |
2,0 |
- |
- |
- |
|
493 |
Гиря, подвешенная к пружине, колеблется по вертикали с амплитудой а=А см. Определить полную энергию Е колебаний гири, если жесткость пружины F=В кН/м. |
4 |
1 |
- |
- |
- |
|
494 |
То же |
3 |
2 |
- |
- |
- |
|
495 |
То же |
2,5 |
4 |
- |
- |
- |
|
496 |
То же |
2 |
3 |
- |
- |
- |
|
497 |
Найти отношение длин двух математических маятников, если отношение периодов их колебаний равно А |
1,5 |
- |
- |
- |
- |
|
498 |
То же |
2,0 |
- |
- |
- |
- |
|
499 |
То же |
2,5 |
- |
- |
- |
- |
|
500 |
То же |
3,0 |
- |
- |
- |
- |
|
501 |
Математический
маятник длиной l=А
м установлен в лифте. Лифт поднимается
с ускорением
|
2,0 |
2,5 |
- |
- |
- |
|
502 |
То же |
2,0 |
5,2 |
- |
- |
- |
|
503 |
То же |
0,5 |
1,5 |
- |
- |
- |
|
504 |
То же |
2,5 |
1,2 |
- |
- |
- |
|
505 |
На концах тонкого стержня длиной l=А см укреплены одинаковые грузики по одному на каждом конце. Стержень с грузиками колеблется около горизонтальной оси, проходящей через точку, удаленную на В см от одного из концов стержня. Определить период колебаний такого физического маятника |
30 |
10 |
- |
- |
- |
|
506 |
То же |
60 |
20 |
- |
- |
- |
|
507 |
То же |
15 |
5 |
- |
- |
- |
|
508 |
То же |
120 |
40 |
- |
- |
- |
|
509 |
Диск радиусом R=А см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить приведенную длину колебаний такого маятника. |
24 |
- |
- |
- |
- |
32
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
510 |
То же |
12 |
- |
- |
- |
- |
|
511 |
То же |
10 |
- |
- |
- |
- |
|
512 |
То же |
|
- |
- |
- |
- |
|
513 |
Математический маятник длиной l1=А см и физический в виде тонкого прямого стержня длиной l2=В см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние центра масс стержня от оси колебаний. |
40 |
60 |
- |
- |
- |
|
514 |
То же |
60 |
90 |
- |
- |
- |
|
515 |
То же |
30 |
45 |
- |
- |
- |
|
516 |
То же |
100 |
150 |
- |
- |
- |
|
517 |
В открытую с обоих концов U - образную трубку с площадью поперечного сечения S=А см2 быстро вливают жидкость плотностью ƍ=В кг/м3 и массой С г. Определить период колебаний жидкости в трубке. |
0,4 |
13600 |
200 |
- |
- |
|
518 |
То же |
0,8 |
1000 |
100 |
- |
- |
|
519 |
То же |
0,2 |
1260 |
150 |
- |
- |
|
520 |
То же |
0,6 |
800 |
50 |
- |
- |
|
521 |
Амплитуда затухающих колебаний маятника за время t=А мин уменьшилась в В раз. За какое время, считая от начального момента, амплитуда уменьшилась в С раз? (Ответ выразить в минутах). |
5 |
2 |
8 |
- |
- |
|
522 |
То же |
10 |
3 |
15 |
- |
- |
|
523 |
То же |
2 |
4 |
20 |
- |
- |
|
524 |
То же |
1 |
5 |
10 |
- |
- |
|
525 |
За время t=А мин амплитуда затухающих колебаний маятника уменьшилась в В раз. Определить коэффициент затухания. |
8 |
3 |
- |
- |
- |
|
526 |
То же |
6 |
4 |
- |
- |
- |
|
527 |
То же |
10 |
5 |
- |
- |
- |
|
528 |
То же |
4 |
2 |
- |
- |
- |
|
529 |
Амплитуда колебаний маятника длиной l=А м за время t=В мин уменьшилась в С раз. Определить логарифмический декремент колебаний. |
1 |
10 |
2 |
- |
- |
33
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
530 |
То же |
0,5 |
3 |
5 |
- |
- |
|
531 |
То же |
1,5 |
15 |
3 |
- |
- |
|
532 |
То же |
2 |
20 |
4 |
- |
- |
|
533 |
Тело массой m=А г совершает затухающие колебания. В течение времени t=В с тело потеряло С % своей энергии. Определить коэффициент сопротивления. |
5 |
50 |
60 |
- |
- |
|
534 |
То же |
10 |
20 |
50 |
- |
- |
|
535 |
То же |
20 |
10 |
70 |
- |
- |
|
536 |
То же |
15 |
30 |
40 |
- |
- |
|
537 |
Определить период Т затухающих колебаний, если период Т0 собственных колебаний системы равен А с и логарифмический декремент колебаний равен В. |
1 |
0,628 |
- |
- |
- |
|
538 |
То же |
2 |
9,314 |
- |
- |
- |
|
539 |
То же |
3 |
0,942 |
- |
- |
- |
|
540 |
То же |
4 |
0,314 |
- |
- |
- |
|
541 |
Под действием силы тяжести электродвигателя консольная балка, на которой он установлен, прогнулась на А мм. При какой частоте вращения якоря электродвигателя может возникнуть опасность резонанса? |
1 |
- |
- |
- |
- |
|
542 |
То же |
2 |
- |
- |
- |
- |
|
543 |
То же |
0,5 |
- |
- |
- |
- |
|
544 |
То же |
0,1 |
- |
- |
- |
- |
|
545 |
Колебательная система совершает затухающие колебания с частотой V=А Гц. Определить частоту собственных колебаний, если резонансная частота В Гц. |
1000 |
998 |
- |
- |
- |
|
546 |
То же |
500 |
497 |
- |
- |
- |
|
547 |
То же |
2000 |
1996 |
- |
- |
- |
|
548 |
То же |
3000 |
2995 |
- |
- |
- |
|
549 |
Определить логарифмический декремент колебаний колебательной системы, для которой резонанс наблюдается при частоте, меньшей собственной частоты V0=А кГц на Δ V=В Гц |
10 |
2 |
- |
- |
- |
|
550 |
То же |
15 |
1 |
- |
- |
- |
|
551 |
То же |
20 |
3 |
- |
- |
- |
|
552 |
То же |
24 |
4 |
- |
- |
- |
34
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
553 |
Пружинный маятник (масса груза m=А г) совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления r=В кг/с. Определить коэффициент затухания. |
100 |
0,02 |
- |
- |
- |
|
554 |
То же |
150 |
0,06 |
- |
- |
- |
|
555 |
То же |
300 |
0,09 |
- |
- |
- |
|
556 |
То же |
800 |
0,08 |
- |
- |
- |
|
557 |
Амплитуды вынужденных колебаний при частоте V1=А кГц и V2=В Гц равны между собой. Определить резонансную частоту. Затуханием пренебречь. |
400 |
600 |
- |
- |
- |
|
558 |
То же |
200 |
300 |
- |
- |
- |
|
559 |
То же |
100 |
400 |
- |
- |
- |
|
560 |
То же |
700 |
1000 |
- |
- |
- |
|
561 |
От источника колебаний распространяется волна вдоль прямой линии. Амплитуда колебаний а=А см. Как велико смещение точки, удаленной от источника на х=(В/С), в момент, когда от начала колебаний прошло время Д периодов. |
10 |
3 |
4 |
0,9 |
- |
|
562 |
То же |
5 |
4 |
5 |
0,7 |
- |
|
563 |
То же |
8 |
1 |
4 |
0,6 |
- |
|
564 |
То же |
6 |
2 |
7 |
0,3 |
- |
|
565 |
Две точки находятся на расстоянии х=А см друг от друга на прямой, вдоль которой распространяется волна со скоростью V=В м/с. период колебаний равен С с. найти разность фаз колебаний в этих точках. |
50 |
50 |
0,05 |
- |
- |
|
566 |
То же |
40 |
60 |
0,07 |
- |
- |
|
567 |
То же |
30 |
200 |
0,01 |
- |
- |
|
568 |
То же |
20 |
90 |
0,03 |
- |
- |
|
569 |
Определить скорость звука в газе (m=А кг/коль) при температуре t=В К (i=С). |
28 |
300 |
5 |
- |
- |
|
570 |
То же |
4 |
10 |
3 |
- |
- |
|
571 |
То же |
17 |
500 |
6 |
- |
- |
|
572 |
То же |
2 |
70 |
5 |
- |
- |
|
573 |
Определить скорость звука в металле плотностью ƍ=А кг/м3 (модуль юнга Е=В ГН/м2). |
2700 |
69 |
- |
- |
- |

 и y=А2
и y=А2 .
Определить ускорение
.
Определить ускорение и y=А2
и y=А2 .
Найти эксцентриситет траектории. А1=А
см, А2=В
см
.
Найти эксцентриситет траектории. А1=А
см, А2=В
см ,
где А=В м,
,
где А=В м,
 С
с-1.
Найти силу, действующую на точку в
момент, когда фаза
С
с-1.
Найти силу, действующую на точку в
момент, когда фаза
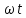 =П/Д.
=П/Д. ,
где А=А см,
,
где А=А см,
 =В
с-1.
В момент когда возвращающая сила в
первый раз достигла значения F=С
мН, потенциальная энергия точки стала
равной Д мкДж. Найти это момент времени.
=В
с-1.
В момент когда возвращающая сила в
первый раз достигла значения F=С
мН, потенциальная энергия точки стала
равной Д мкДж. Найти это момент времени. =В
м/с2.
Определить период Т колебаний маятника.
=В
м/с2.
Определить период Т колебаний маятника.