
Банк задач, механика , молекулярная физика и термодинамика, 1 семестр
.docx
МИНИСТЕРСТВО РЫБНОГО ХОЗЯЙСТВА СССР
МУРМАНСКОЕ ВЫСШЕЕ ИНЖЕНЕРНОЕ МОРСКОЕ УЧИЛИЩЕ
ИМЕНИ ЛЕНИНСКОГО КОМСОМОЛА
КАФЕДРА ФИЗИКИ
БАНК ЗАДАЧ ПО ФИЗИКЕ
Часть 1
Составитель В.Н. Подымахин
Мурманск
1985 г.
Составитель - Владимир Никанорович Пдымахин, канд. техн. наук, доцент кафедры физики Мурманского высшего инженерного моского училища имени Ленинского комсомола.
Банк задач рассмотрен и одобрен кафедрой 12 мая 1984 г. протокол № 9
Введение
Применение банка задач в учебном процессе кафедры ставит своей целью долю самостоятельной работы курсантов при изучении курса физики и улучшить межсессионный контроль за ходом самостоятельной подготовки. Этого можно достичь путем индивидуализации домашних заданий, уменьшения времени на проверку решений задач и оперативного промежуточного контроля результатов.
Перечисленные действия, а также выдача набора задач каждому курсанту на семестр осуществляются с помощью ЭВМ по специальной программе.
Всего представлено пять тем первой части курса общей физики:
1 – физические основы механики;
2 – силы в механике;
3 – механические колебания и волны;
4 – молекулярная физика;
5 – физические основы термодинамики.
Банк задач (часть 1) содержит 93 задачу. Для каждого четверки задач (1-4, 5-8 и т.д.) условия одинаковы и задачи отличаются только численными значениями входящих в них физических параметров А, В, С, Д, Е).
Задача считается решенной, если получен правильный числовой ответ, отличающийся от заложенного в ЭВМ не более чем на 5%.
Рекомендуемая литература
1. Новодворская Е.М., Дмитриев Э.М. методика проведения упражнений по физике во втузе – М.: Высш. Школа, 1981. – 318 с.
2. Фиргант Е.В. руководство к решению задач по курсу общей физики: Учеб. Пособие для студентов втузо. – М.: Высш. школа, 1977. – 361 с.
3. Пойа Д. Как решать задачу. – М.: Высш. школа, 1959. – 240 с.
4
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
1 |
Две автомашины движутся по двум прямолинейным взаимно перпендикулярным дорогам по направлению к перекрестку с постоянными скоростями V1=А км/ч и V2=В км/ч. Перед началом движения первая машина находилась на расстоянии S1=С км от перекрестка, вторая – на расстоянии S2=Д км. Через какое время после начала движения расстояние между машинами будет минимальным? (Ответ дать в секундах) |
50 |
100 |
100 |
50 |
- |
|
2 |
То же |
60 |
100 |
100 |
50 |
- |
|
3 |
То же |
60 |
90 |
100 |
50 |
- |
|
4 |
То же |
60 |
120 |
100 |
50 |
- |
|
5 |
Две материальные точки движутся согласно уравнениям x1=At + Dt2 – Ct3 и x2=2t – Dt2 + t3, где x – в метрах, t – в секундах. |
4 |
8 |
16 |
4 |
1 |
|
6 |
То же |
6 |
10 |
12 |
4 |
2 |
|
7 |
То же |
3 |
15 |
12 |
15 |
2 |
|
8 |
То же |
30 |
7 |
12 |
14 |
2 |
|
9 |
Материальная точка движется прямолинейно. Уравнение движения имеет вид: x=Аt + Bt3 (длина – в метрах, время – в секундах). Найти значение среднего ускорения за первые С с движения. |
3 |
0,06 |
3 |
- |
- |
|
10 |
То же |
4 |
0,5 |
2 |
- |
- |
|
11 |
То же |
2 |
0,02 |
10 |
- |
- |
|
12 |
То же |
2,5 |
0,01 |
100 |
- |
- |
|
13 |
Точка движется по прямой согласно уравнению x=Lt – Bt3 (длина – в метрах, время в секундах). Определить среднюю скорость движения точки в интервале времени от t1=С с до t2=Д с. |
6 |
0,125 |
2 |
6 |
- |
|
14 |
То же |
6 |
0,222 |
2 |
6 |
- |
5
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
15 |
То же |
6 |
0,08 |
2 |
6 |
- |
|
16 |
То же |
10 |
0,25 |
2 |
6 |
- |
|
17 |
Точка движется по прямой согласно уравнению x=At – Bt3 (длина – в метрах, время – в секундах). Определить среднюю скорость перемещения точки в интервале времени t1=С с до t2=Д с. |
6 |
0,125 |
2 |
6 |
- |
|
18 |
То же |
6 |
0,22 |
2 |
6 |
- |
|
19 |
То же |
6 |
0,08 |
2 |
6 |
- |
|
20 |
То же |
12 |
0,25 |
2 |
6 |
- |
|
21 |
Движение двух материальных точек выражается уравнениями x1=A + Вt – Ct2 и x2=2 + Dt + t2 (длина – в метрах, время в секундах). Какова скорость первой точки в момент времени, когда скорости этих точек будут одинаковы? |
20 |
2 |
4 |
2 |
0,5 |
|
22 |
То же |
40 |
5 |
3 |
6 |
1 |
|
23 |
То же |
30 |
4 |
4 |
5 |
1 |
|
24 |
То же |
25 |
3 |
8 |
2 |
2 |
|
25 |
Движение двух материальных точек выражается уравнениями x1=A + Вt – Ct3 и x2=2 + Dt + t3 (длина – в метрах, время в секундах). Каково ускорение второй точки в момент времени, когда скорости этих точек будут одинаковы? |
20 |
2 |
4 |
2 |
0,5 |
|
26 |
То же |
40 |
2 |
4 |
1 |
0,5 |
|
27 |
То же |
30 |
5 |
3 |
4 |
1 |
|
28 |
То же |
25 |
3 |
8 |
2 |
2 |
|
29 |
Материальная точка движется прямолинейно. Уравнение движения имеет вид: x=Аt + Bt2 + Ct3 (длина – в метрах, время – в секундах). Какова средняя скорость движения точки в интервале времени от Д с до Е с? |
3 |
6 |
2 |
1 |
2 |
|
30 |
То же |
3 |
4 |
5 |
2 |
4 |
|
31 |
То же |
2 |
3 |
4 |
1 |
5 |
|
32 |
То же |
1 |
2 |
3 |
4 |
0 |
6
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
33 |
Лодка, идущая через реку на веслах, движется относительно воды со скоростью V1=А м/с. Течение реки имеет скорость V2=В м/с. Найти
полную скорость лодки, если она движется
под углом
|
2 |
1 |
90 |
- |
- |
|
34 |
То же |
2 |
1 |
45 |
- |
- |
|
35 |
То же |
2 |
1 |
135 |
- |
- |
|
36 |
То же |
2 |
1 |
60 |
- |
- |
|
37 |
Корабль идет на запад со скоростью V1=А м/с. Ветер дует с юго-запада со скоростью V2=В м/с. какую скорость ветра зарегистрируют приборы, расположенные на корабле? |
6,5 |
3,5 |
- |
- |
- |
|
38 |
То же |
6,0 |
4,0 |
- |
- |
- |
|
39 |
То же |
6,3 |
3,75 |
- |
- |
- |
|
40 |
То же |
5 |
3 |
- |
- |
- |
|
41 |
Точка движется по окружности радиусом R=А м. Закон ее движения S=E-Ct2, где S – в метрах, t – в секундах. Найти, в какой момент времени нормальное ускорение точки аn=Д м/с2. |
4 |
8 |
2 |
9 |
- |
|
42 |
То же |
4 |
10 |
3 |
36 |
- |
|
43 |
То же |
4 |
6 |
4 |
6,25 |
- |
|
44 |
То же |
5 |
12 |
5 |
20 |
- |
|
45 |
Точка движется по окружности радиусом R=А м. Закон ее движения S=В-Ct2, где S – в метрах, t – в секундах. Найти, полное ускорение точки в момент времени, когда нормальное ускорение аn=Д м/с2. |
4 |
8 |
2 |
9 |
- |
|
46 |
То же |
4 |
10 |
3 |
36 |
- |
|
47 |
То же |
4 |
6 |
4 |
6,25 |
- |
|
48 |
То же |
5 |
12 |
5 |
20 |
- |
|
49 |
Материальная точка движется по окружности радиусом R=А м согласно уравнению S=Вt -Ct3, (длина – в метрах, время – в секундах). Найти нормальное ускорение точки в момент времени t=Д с. |
2 |
8 |
0,2 |
3 |
- |
7
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
50 |
То же |
2 |
16 |
0,4 |
3 |
- |
|
51 |
То же |
2 |
5 |
0, |
4 |
- |
|
52 |
То же |
4 |
5 |
0,1 |
4 |
- |
|
53 |
Материальная точка движется по окружности радиусом R=А м согласно уравнению S=Вt -Ct3, (длина – в метрах, время – в секундах). Найти полное ускорение точки в момент времени t=Д с. |
2 |
8 |
0,2 |
3 |
- |
|
54 |
То же |
2 |
16 |
0,4 |
3 |
- |
|
55 |
То же |
2 |
5 |
0,1 |
4 |
- |
|
56 |
То же |
4 |
15 |
0,1 |
6 |
- |
|
57 |
По
дуге окружности радиусом R=А м движется
точка. В некоторый момент времени
нормальное ускорение точки аn=В
м/с2.
Вектор полного ускорения образует в
этот момент с вектором нормального
ускорения угол
|
10 |
4,9 |
60 |
- |
- |
|
58 |
То же |
12 |
5,33 |
45 |
- |
- |
|
59 |
То же |
9 |
4 |
30 |
- |
- |
|
60 |
То же |
10 |
4 |
70 |
- |
- |
|
61 |
По
дуге окружности радиусом R=А м движется
точка. В некоторый момент времени
нормальное ускорение точки аn=В
м/с2.
Вектор полного ускорения образует в
этот момент с вектором нормального
ускорения угол
|
10 |
4,9 |
60 |
- |
- |
|
62 |
То же |
12 |
5,33 |
45 |
- |
- |
|
63 |
То же |
9 |
4 |
30 |
- |
- |
|
64 |
То же |
10 |
4 |
70 |
- |
- |
|
65 |
Определить
в момент времени t=А с полное ускорение
точки, находящейся на ободе колеса
радиусом R=В м, вращающегося согласно
уравнению
|
3 |
0,5 |
2 |
0,2 |
- |
8
|
№ п/п |
ЗАДАЧА |
ПАРАМЕТРЫ |
||||
|
А |
В |
С |
Д |
Е |
||
|
66 |
То же |
4 |
0,5 |
2 |
0,1 |
- |
|
67 |
То же |
2 |
1 |
4 |
1 |
- |
|
68 |
То же |
4 |
0,2 |
1 |
0,1 |
- |
|
69 |
Определить в момент времени t=А с нормальное ускорение точки, находящейся на ободе колеса радиусом R=В м, вращающегося согласно уравнению |
3
|
0,5 |
2 |
0,2 |
- |
|
70 |
То же |
4 |
0,5 |
2 |
0,1 |
- |
|
71 |
То же |
2 |
1 |
4 |
1 |
- |
|
72 |
То же |
4 |
0,2 |
1 |
0,1 |
- |
|
73 |
Диск
радиусом R=А м вращается согласно
уравнения
|
0,2 |
3 |
-1 |
0,1 |
10 |
|
74 |
То же |
0,4 |
3 |
+1 |
0,2 |
5 |
|
75 |
То же |
0,1 |
10 |
-2 |
0,1 |
15 |
|
76 |
То же |
0,1 |
10 |
+2 |
0,1 |
5 |
|
77 |
Диск
радиусом R=А м вращается согласно
уравнения
|
0,2 |
3 |
-1 |
0,1 |
10 |
|
78 |
То же |
0,4 |
3 |
+1 |
0,2 |
5 |
|
79 |
То же |
0,1 |
10 |
-2 |
0,1 |
15 |
|
80 |
То же |
0,1 |
10 |
+2 |
0,1 |
5 |
|
81 |
На цилиндр, который может вращаться вокруг горизонтальной оси, намотана нить. К концу нити привязали грузик и предоставили ему возможность опускаться. Двигаясь равноускоренно, грузик за время t=А с опустится на h=В м. Определить угловое ускорение цилиндра , если его радиус r=С см. |
3 |
1,5 |
4 |
- |
- |
|
82 |
То же |
4 |
1 |
5 |
- |
- |
|
83 |
То же |
2 |
2 |
2 |
- |
- |
|
84 |
То же |
4 |
2 |
3 |
- |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

 =С
град к направлению течения реки.
=С
град к направлению течения реки. =С0.
Найти скорость движения точки.
=С0.
Найти скорость движения точки. =С0.
Найти тангенциальное ускорение точки.
=С0.
Найти тангенциальное ускорение точки.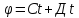 3
3 3 .
Определить тангенциальное ускорение
точек на окружности диска в момент
времени t=Е
с.
3 .
Определить тангенциальное ускорение
точек на окружности диска в момент
времени t=Е
с.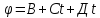 3 .
Определить полное ускорение точек на
окружности диска в момент времени t=Е
с.
3 .
Определить полное ускорение точек на
окружности диска в момент времени t=Е
с.