
Физика вод суши / Хватаем
.doc|
1. Физические свойства воды и диаграмма её агрегатных состояний. П |
2. Роль физико-механических процессов в изменчивости свойств снежного покрова. 3. Физико-механические и тепловые процессы, протекающие в снежном покрове, и их роль в образовании лавин. Снежный покров – слой снега, лежащий на поверхности земли и образовавшийся при снегопадах. К физ факторам отн-ся режеляция, рекристаллизация, возгонка и сублимация, гелио- и гео- тепловые воздействия. К меха-м факторам относятся сила тяжести и ветер. 1.Режеляция (повторное смерзание) заключ-ся в плавлении и повторном смерзании ледяных кристаллов, образующих снежинки, под влиянием удельного давления. Протекает с заметной интенсивностью лишь при t, близкой к О °С, т. е. при t, при кот не требуется большого уд-го давления, чтобы вызвать плавление льда. Уд.давление мб обусловлено высотой снежн покр, возник-ем добавочного давления при острых углах и лучах снежинок. Образова-ся вода выдавливается в соседние места и снова замерзает. 2. Рекристаллизация –физ процесс, при кот атомы молекул перескакивают с кристаллической решетки 1 кристалла на решетку др, и обусловливают срастание отдельных кристаллов (снежинок). Хаар-р и v процесса зависят от ориентации пространственных решеток и тенденции перехода системы из менее в более уст-е сост. Большое зерно устойчивее малого. 3.Возгонка-процесс перехода вещ-ва из твердой фазы в газообразную, минуя жидкую. 4.Сублимация- процесс кристаллизации вещ-ва из пара. 5.Фирнизация снега -процесс округления кристалликов льда и увеличения их объема, т.е. процесс превращения свёжевыпавшего снега, состоящего из отд-х снежинок с их своеобразной формой, в бесформенную массу ледяных зерен, сначала мелких, а затем все более и более крупных. Он наблюдается при изотермии и активизируется при наличии температурной стратификации. 6.Повторное таяние кристаллов льда и замерзание воды способствует фирнизации снега. Таяние кристаллов начинается с их выступающих частей: углов, лучей, ребер. При повторном таянии кристаллические зерна увеличиваются в размерах за счет попадания на них капелек воды с соседних кристалликов. При этом в снежном покрове увеличиваются поры и на их стенках осаждается иней, обусловленный сублимацией. Процесс ускоряется за счёт гравитационной воды, проникаю сверху в ре-те таяния верхнего слоя СП.
Роль. Мокрый СП представляет собой трехфазную систему, состоящую из ледяных кристаллов, воды и воздуха, содержащего водяной пар. Соотношение фаз для снега является неустойчивым и все время меняется в связи с изменением его плотности под воздействием физико-мех-х процессов, протекающих в СП, и особенно в период снеготаяния. Как раз в этот период водные свойства снежного покрова имеют особенно большое значение для прогноза схода лавин. Из общих физ процессов, происходящих в СП, большое значение имеет фирнизация снега. В горных условиях фирнизация снега обусловливает образование лавин, льда ледников. В наст. время считается установленным, что снежные лавины(СЛ) образуются чаще всего на склонах гор крутизной порядка 20- 40°. Лавина образуется при нарушении устойчивости СП из-за уменьшения сил сцепления с подстилающей поверхностью и коэф внутреннего трения в нижних его горизонтах. В процессе метаморфизма кристаллов льда образуются глубинный иней (изморозь) и рыхлый крупнозернистый плотно слежавшийся снег. Процесс разрыхления в нижнем горизонте сопровождается оседанием СП, при котором теряется его связь с подстилающей поверхностью и, следовательно, происходит сползание по склону снежного пласта. Лавины возникают также при резких суточных колебаниях t воздуха. В этом случае причиной нарушения устойчивости снежного покрова являются образовавшиеся в нем трещины при темп-ом сокращении сплошной снежной доски (плотного снега). Другой вид лавины образуется из свежевыпавшего сухого снега после обильного снегопада. Не успев уплотниться, свежевыпавший снег соскальзывает по старому, набрав скорость, вовлекает в движение нижележащие слои. Другим видом сухой лавины является лавина, образующаяся из метелевого снега при скорости ветра 5 - 1 0 м/с. Когда тем-ра воздуха переходит через 0 °С со склонов сходят так называемые мокрые лавины. Они образуются при выпадении мокрого снега либо в период снеготаяния (или дождя), когда талью воды просачиваются до грунта и затем выступают в роли смазочного материала между грунтом склона и снегом. 36. Таяние зависит от теплоты, поступающей в СП из атмосферы, и от подстилающей пов-ти. СП хар-ся значительной пространственной неоднородностью Структура меняется во времени. Неоднородность толщины, плотности, строения СП обусловливает изменчивость пористости, воздухопроницаемости, кот тоже важны при таянии. Т.к. снег явл средой, меняющей агрегатное сост при изменении t, то процесс таяния делится 1)период нагревания до 0С 2) период собственного таяния снега. |
|
6. Основные функциональные зависимости температурного поля. Каждая точка природных объектов (грунт, лед, снег, вода) и инженерных сооружений (плотина, разделяющая стенка, трубопровод) хар-ся t. Если t тела изменяется от точки к точке, то оно может быть охарактеризовано пространственным t полем, а если t изменяется и во времени, то пространственно- временным. ТП может быть представлено виде функциональной зависимости t =f1(x, y, z, τ). ТП -совокупность значений t для всех точек пространства в данный момент времени. ТП поля подразделяют на стационарные и нестационарные. Если t тела является функцией координат и времени, что соответствует зависимости t =f1(x,y,z,τ), то это нестационарное. В том случае, когда t тела с течением времени не изменяется (dt./dτ = 0 ) и является функцией только координат, ТП будет стационарным: t = f 2(x, y, z). Различают ТП трехмерные (пространственные), двухмерные (плоские) и одномерные (линейные). К первым относятся поля, описываемые зависимостями t =f 1(x, y, z, τ) и t = f 2(x, y, z), ко вторым - поля, описываемые зависимостями: t = f3(x,y,τ) и t = f4(x,y). к третьим - поля, описываемые зависимостями: t = f5(x,τ) и t = f6(x). Изотерма-линия точек с одинаковой t. Для них dt=ɗt/ɗx *dx+ ɗt/ɗy *dy=0. Если выделить расположенные рядом изотермы с дt и проследим расстояние дn, то оно окажется различным. Отношение перепада дt к дn по нормали n-градиент t: grad t =Lim дt/дn=ɗt/ɗn. Градиент больше там, где расст-е меньше. Градиент – вектор, направленный по нормали к изотерме в сторону возрастания t |
5 |
|
9. Теплопередача и теплоотдача теплопроводностью, конвекцией, испарением, лучистым теплообменом, изменением агрегатного состояния вещества. Их количественная оценка. Теплопередача – совокупность явлений передачи теплоты из более нагретой подвижной среды в другую, менее нагретую, через разделяющую их твёрдую стенку. Теплоотдача – совокупность явлений переноса теплоты между поверхностью тв тела и жидкой или газообразной подвижной средой (нет стенки). 1. Теплопроводностью. Фурье, занимаясь изучением теплопроводности в средах, вывел закон : тепловой поток прямо пропорционален градиенту температуры: q= -λ ɗt/ɗn, n – нормаль к изотермической поверхности, λ-коэфф теплопроводности (пропорциональности) (зависит от t, p, влажности). Выведен экспериментально Q=qF= -λ(ɗt/ɗn)F. Q-тепловой поток, q-уд т.п., F-площадь. (количество теплоты, проходящее в ед времени через ед площади изотермической пов-ти называется плотностью теплового потока q (уд т.п.)). 2. Конвекцией. Qк(Конвекция - вид теплопередачи, при котором энергия переносится потоками жидкости или газа.) Происходит в рез-те перемещения частиц теплоносителя и наблюдается только в ж и газ средах. 1). Свободная- Перемещение частиц жидкости в силу изменения их плотности из-за нагревания или охлаждения, изменения концентрации. (например, охлаждение воды в сосуде сверху, тогда возникнет перенос частиц воды снизу вверх) 2). Вынужденная – обусловлена турбулентным перемешиванием водных или воздушных масс потока. Происходит молярный перенос водных масс, а не молекулярный (как в св) т.е. перенос больших объёмов жидкости. (например, ветровое перемешивание). \\\ Конвективный теплообмен в природе определяется разницей между t подстилающей поверхности (tп) и t находящейся над ней жидкости или газообр среды (θ), в кот имеет место молярный перенос теплоты. По закону Ньютона можно опр кол-во темплоты Qк (вт/м2), теряемое 1 м2 этой пов-ти в ед времени: Qк=α(tп- θ). α-коэф теплоотдачи от пов в среду. (опр экспер-но, зависит от шероховатости, скорости дв, t и физ пар-ов окр среды). (Ф: Проскурякова, Браславского). 3. Лучистым теплообменом. Природа манитоэлектическая. Часть энергии тела, определяемая температурой его поверхности, преобразуется в энергию теплового излучения и уже в таком виде передаётся в окружающее пространство. Встречая на пути др тело, лучистая энергия частично отражается от его поверхности и частично поглощается им, т.е. проникает на некоторую глубину, зависящую от прозрачности тела. Виды излучения (по ув длины волны): космическое, рентгеновское, ультраифолетовое, видимое, тепловое, радио-волны. \\\ Если пов-ть тела поглощает все падающие на неё лучи, то это абс чёрн тело; если отражает лучи – абс белое; если пропускает лучи-абс прозрачное. Закон Стефана-Больцмана: Qиз= σ0 T^4, (σ0-5,67*10^-8-коэф излучение АЧТ, постоянная С-Б, Т-тем-ра). Это зависимость для опр теплового потока при передаче теплоты излучением АЧТ. Реальные тела не АЧТ, поэтому Qиз= ε σ0 T^4, ε-степень черноты серого тела (0-1). \\ Разность между поглащ суммарной радиацией и эф излучением земной пов-ти наз-ся тепловым балансом (радиационным). QR=(1-А)(Qп.р+qр.р.)-Iэф. А-альбедо (хар-ет отражат спос-ть пов-ти, %, это отношение интенсивности радиации, отражённой данной пов-тью к интенсивности радиации, падающей на неё), Qп.р+qр.р.– суммарная солнечная радиация; Iэф – эф излучение при облачности (это разность: собственное излучение пов-ти Земли-излучение атмосферы). 4. Изменение агр сост вещ-ва. При испарении воды, таянии снега и льда, происходит поглощение теплоты из окр среды (сток). При конденсации водяного пара, замерзании воды и грунта, происходит выделение теплоты в окр среду (исток). \\\ Количественная оценка при испарении (теплоотдача в атмосферу) воды: закон Дальтона Qи=Lи ρ E, Lи-уд теплота испарения =2500 кДж/(кг*град), Е – слой испарившейся воды в ед времени (много формул, Е=ε(e0-e2) Зайков, е0-давление насыщ вод пара в воздухе при t испаряющей пов-ти, е2-парциаольное давление вод пара 2м. ε=0.14(1+0.72w2) – интенсивность испарения, w2-скорость ветра. Qи=4,1(1+0.72w2)(е0-е2) \\\ Кол оценка теплообмена при кристаллизации воды (плавлении льда) Qкр=Lкр ρ h; Lкр=33,5*10^4 Дж/кг, h-слой замёрзшей воды. Кол оценка теплопередачи (это от среды к среде через тв стенку). От воды к стенке: Q=α1(t воды-t нижней пов ст), от стенки к воздуху:Q=α2(t верхн пов ст-θ2(возд)). По закону Фурье: Q= (λ/δ)F(t н.п.- t в.п.), δ-материал стенки. q=(tв-θ)/(1/α1+ δ/λ +…+1/α2). 1/α-внешнее термическое сопротивление, δ/λ-термическое сопротивление стенки, q-уд тепл поток.
|
7. Статистическое и динамическое давление льда. Показать необходимость их учёта на примере сооружения по защите СПб от наводнений. Давление лед-го покрова (ЛП) на сооружения при повышении его температуры (при расширении)- статическим давлением. Статическое давление на ГС д.б. учтено, т.к. оно может составлять порядка 106 Н/м2. Также, СД это нагрузки от примерзего ЛП к сооружению при изменении уровня воды (к свае). Сначала высчитывали по форумуле Р=0,9hл (tн+1) (tн (tн+1)2/т’)1/3, но потом нашли ошибку. Проскуряков предложил метод расчета статического давления ЛП на ГС, основанный на уравнениях Навье-Стокса . При сжимающем напряжении P0<5*104 H/m2 лед ведет себя как упругое тело. После того, как напряжение превысит этот предел, деформации во льду подчиняется закону Ньютона: Pкас=µ*ɗv/ɗn , где µ-коэф.вязкости льда, v- cкорость деформации льда, n-нормаль. \\ Это означает, что лед течет (т.е. пластич тело). => лед при напряжении P0<5*104H/m2 - жидкость. (Бингамовоя жидкость, а ее движение – ползущее). Т.к. лед обладает текучестью, то рассчитать напряжение можно по ур-ям гидродинамики: Pxx=P0-P+2µ ɗvх/ɗx-2/3µ div(v),где Pxx ,Pyy ,Pzz – нормальные напряжения, действующие на площадках, перпендикулярных соответственно осям x,y,z ;P-гидромех.давление ; vx,vy,vz-проекции скорости движения соответственно на оси x,y,z. \\\ Для несжимаемой нерасширяющейся жидкости div v=0. После преобразований P’xx = -∑(P0+4µɑ*(дt/дτ)i)*дz, (сумма от 0 до hл). Для практич пользования: Ft=hmaxkлP’xx , где hmax-маx толщина ледяного покрова, kл-коэф, учитывающий протяженность ЛП , P’xx-давление от ЛП за счет пластической и упругой деформации. Т.о., нагрузка льда на берега зависит от толщины ледяного покрова и скорости изменения его температуры, с увеличением которой интенсивность давления увеличивается. Стат нагрузка (СН) от ЛП, находящ на плаву Pxx=(P1+P2+P3+P4)Ω, P1=ɑ1v2-напряжение от трения потока воды о нижнюю пов-ть ЛП, P2= ρh’лI-от действия силы тяжести на массу льда, выступающ над водной пов-ю. P3= ɑ2 ω2- от трения воздушн потока о верхнюю пов-ть ЛП. P4=5*10-4 hл v2в/L-от действия потока воды на кромку ЛП. Нагрузка от примёрзшего к сооружению ЛП при изменении уровня воды: Происходит изгиб, приводящий к появлению вертикального усилия => разрушение сооружения. Pд=kf Rf h2л, hл-max толщина ЛП, Rf- предел прочности льда на изгиб, kf=0.6+0.15*D/hл .D-диаметр опоры. Весной нужно откалывать лёд вокруг сваи. Н
Существенную помеху представляли навалы льда также при эксплуатации причерноморской и прибайкальской железных дорог, при создании линий электропередач, строительстве и эксплуатации сооружений по защите г.СПб от наводнений и др. Дамба рассматрвиается как берег, она должна выдержать навалы льда. Булыжники еперд дамбой-как щиты, которые останавливают нагромождение; иначе навалы повредят саму дамбу, автодороги. |
|
8. Закон теплопроводности. Использование его для решения практических задач. Тепловой поток (ТП) – количество теплоты, проходящее в ед времени через изотермическую пов-ть. Направлен в сторону менее нагретой части среды. ТП, проходящ через ед пов-ти – интенсивность ТП. Кол-во теплоты, проходящее в ед времени через ед площади изотермической пов-ти – плотность ТП (уд ТП)-q. Французский ученый Фурье, изучая перенос теплоты в средах, открыл закон, согласно которому уд ТП прямо пропорционален градиенту температуры: q = -λ*(dt/dn), λ-коэф теплопроводности. Как и градиент температуры, удельный ТП q - вектор, направлен он по нормали п; положительным принято считать направление в сторону убывания температуры. Векторы градиента тем-ры и удельного ТП направлены в противоположные стороны. Зная q, можно опр-ть тепловой поток, проходящ через площадь F, выделенную на изотермич пов-ти: Q=qF. В задачах з.Фурье используется для определения удельного потока тепла, потери тепла водоёма за сутки, граничных условий (3?). Например, дана задача: найти поток тепла через многослойную стенку. 4 слоя: 1-вода, 2-лёд,3-снег,4-воздух. Для 1 и 4 слоя находим по з.Ньютона, т.к. движущаяся среда, для 2 и 3 по Фурье, т.к. тв тело. В итоге складываем все уравнения и находим удельный потом тепла через многосл стенку. |
12. Условия однозначности при решении уравнения теплопроводности. Чтобы решить с помощью диф-ого уравнения теплопроводности задачу, нужноо знать условия однозначности (УО), кот позволяют различать задачу одну от другой. УО состоят: 1)Геометрические У-характер-ют формы и размеры тела. 2)Физические У- хар-ют физ свойства вещества, слогающие тело; 3) Краевые (временные) У- хар-ют распределение t в рассматр-м теле в начальный момент времени (нач.условия). 4) Граничные У- хар-ют тепловое взаим-е рассм-го тела с окр его средой.1. НУ заключаются в задании распределения значений t в нач момент времени (τ = 0). Они должны быть заданы в виде функций: tτ=0 = f1 (х, у, z) - для пространственной задачи, для плоской и линейной без y и z соотв. 2.ГУ . В зав-ти от способа задания бывают 1,2,3,4 рода. А). ГУ 1го рода - задается t во всех точках поверхности тела в течение времени τ: tп=f4 (x,y,z,τ). Б). ГУ2го рода - задается удельный тепловой поток по з.Фурье через поверхность тела в течение времени τ: qп= -λɗt/ɗn; qп=f5(x,y,z,τ). B)ГУ3го рода -задание t поверхности тела и окр его среды (tс) и задании теплообмена (коэф теплоотдачи) между пов-ю этого тела и окружающей средой по з.Ньютона. qп= α(tп-tс); Приравнивая (Ф=Н): ɗt/ɗn |n= - ɑ/λ (tп-tс ), ɗt/ɗn |n –градиент t у пов-ти и по нормали к ней. Г). ГУ4го рода -задается равенство t на поверхности раздела 2х тел или тела с окр средой при подходе к ней с 2х сторон, а также удельных тепловых потоков по з.Фурье в предположении, что между этими телами осуществляется идеальный контакт. t1 = t2 и q1 = q2. |
|
10. Вывод дифференциального уравнения теплопроводности для потока жидкости, его частные случаи. 11. Стационарное температурное поле и дифференциальное уравнение, его описывающее. Вывод этого уравнения. О |
14. Уравнение теплового баланса для открытого водоёма. ∑Q=QR+QK+Qи+Qпр+Qгр+Qос+… , QR- радиационный баланс, Qк-конвективный теплообмен, Qи-испарение воды, Qпр-воды притоков или промышл воды, Qд-теплообмен между водой и дном, Qгр-грунтовые воды, Qос-осадки.\\\ Метод теплового баланса для оценки испарения с водной поверхности впервые применен Е.Шмидтом. Метод предусматривает исп-е ур-я теплового баланса (ТБ). QR=ρLиE+P+B, где QR- радиационный баланс, ρ- плотность воды, Lи-удельная теплота испарения, Е- слой испарившейся воды, Р-количество теплоты, обусловленное турбулентным теплообменом между водной пов-ю и воздухом, В-кол-во теплоты, обусловленное теплообменом между водной пов-ю и нижележащими слоями воды. Это ур-е выражает закон сохранения и превращения энергии. Согласно этому закону, разность между поступающей тепловой энергией в водоем и уходящей из него д.б. равна изменению кол-ва теплоты водной массы водоема за рассматриваемый промежуток времени. Применительно к поверхности воды эта разность тепловой энергии =0. С учетом отношения Боуэна, устанавливающего связь между кол-м теплоты, получаемой водной пов-ю от воздуха при турбулентном теплообмене Р, и кол-м теплоты, затрачиваемой на испарение ρLиE. Относительно испарения ур-е примет вид: E=(R-B)/[Lи(1-ɑ dt/dq)] , где ɑ=ср/Lи, ср-удельная теплоемкость воздуха при пост давлении. Метод ТБ не нашел широкого применения в гидрологической практике, связанной с расчетами испарения. Основная причина его малой применимости заключается в отсутствии данных непрерывных градиентных наблюдений за метеорологическими элементами над акваторией водоемов, а также в отсутствии наблюдений за теплообменом В в их водной массе. |
|
|
16. Уравнение Лапласа и методы его решения: а). метод электротепловых аналогий; б). графический метод (закон рисунка). Ур-е ɗ2t/ɗx2+ɗ2t/ɗy2+ɗ2t/ɗz2=0; Это ур-е описывает стационарное t-е поле, т.е. поле, не меняющихся со временем. А) метод электротепловых аналогий. В основе - аналогия математич записи 2-х различных физ.явлений. С одной стороны - явление теплопроводности фильтрации, диффузии и тд., а с др -электропроводности в электропроводном материале. 1).З.Фурье: q=-λ ɗt/ɗn; З.Дарси q= -k ɗН/ɗn; З.Фика q=-D ɗS/ɗn; 2).З.Ома I=-σ ɗU/ɗn. q-уд поток теплоты, S-концентрация, H-напор, U-эл.потенциал. д/электрическое поле : д2U/дх2+д2U/ду2=0. Если перейти к ур-ям Лапласа для 2х мерного поля: тепловое: ɗ2t/ɗx2+ɗ2t/ɗy2=0, диффузное: ɗ2S/ɗx2+ɗ2S/ɗy2=0; фильтрующих вод (с Н); электрическое (с U). Используя эту аналогию, на практике по данным эл.поля (на модели) находят t-е поле и поток теплоты. |
|
17. Расчёт средней по глубине температуры воды неподвижного водоёма (метод изоклин). В |
18. Уравнение теплового баланса для открытых водоёмов и метод его решения (метод суперпозиции). Метод предложен А.П. Пеховичем и В.М. Жидких. Предусматривает исп-е диф ур-я теплопроводности для немпроточного водоёма ɗt/ɗτ=ɑт ɗ2t/ɗz2 , где ɑт= λ/(сρ)-коэф турбулентной температуропроводности. Принцип суперпозиции (С) состоит в том , что если составляющие сложного процесса воздействия взаимно не влияют друг на друга, то результирующий эффект от этих воздействий будет представлять собой сумму эффектов, вызываемых каждым воздействием в отдельности. Этот принцип строго применим к системам, поведение которых описывается линейным соотношением. Разложение краевых условий на простые процессы заключается в следующем: 1)Сумма значений начальной t (t01+t02+…) и тепловых условий на поверхности воды (Qп1+Qп2+…) и на дне (Qд1+Qд2+…) для слагаемых задач была равна начальной температуре t0=t01+t02+t03+… и тепловым условиям на пов-ти Qп= Qп1+Qп2+… и на дне Qд= Qд1+Qд2+… в основной задаче. (Граничные условия , т.е. при т>0 Сумма(от n до 1) Q=сумма Q1+суммаQ2+…) 3) Значения коэф-в температуропроводности ɑт, теплопроводности λт и теплоотдачи α должны быть одинаковыми.\\\ Пехович и Жидких разработали 19 аналитических решений для простых задач. Безразмерные координаты графиков в зависимости от № задачи представлены искомой относительной избыточной t: Θи1=(t-tп)/(t0-tп); Θи2=(t-Θ2)/(t0-Θ2); Θи3= (t-t0)/(bτ); Критерием Фурье F0=ɑтτ/h2, Критерием Био Bi=α h/λт, и относительной глубиной μ=z/h, где t,t0,tп иΘ2-соответственно температура воды в точке, начальная и на поверхности, и температура воздуха на высоте 2м; b- коэф. При линейном задании температуры поверхности воды или воздуха; ɑт-коэф.турбулентной температуропроводности; τ- время; z и h –переменная и полная глубина водохранилища; α и λт –соответственно коэф.теплоотдачи и турбулентной теплопроводности. Порядок решения задачи: 1. Раскладываем тепловой потом, приходящий на пов-ть, на 3 составляющие (1-->2,3,4). 2. Для каждой из 3х задач уст-ем нач и гранич условия. (t0-нач, Qi-граничн+ɗt/ ɗz |z=h =0). Сумма нач и гранич условий задач = условию изначальной задачи. Ищем рисунки, кот совпадают с усс-ми (3 шт, Мишон). По рисунку находим формулу для расчёта.
|
|
19. Гидротермический расчёт водохранилищ-охладителей. Поясните принцип работы других типов охладителей воды. Гидроэнергетике принадлежит ведущая роль в комплексном исп-ии водных ресурсов. ГЭС экологически чистая, но предпочтение отдают ТЭС и АЭС (дольше строить, зав-ть от водности водотока). В качестве охладителей используют градирни, брызгальные бассейны и водохранилища. Преимущ-во отдают водохранилищам-охладителям (В-О), тк меньше затрат на перекачку воды, комплексное исп-е водоёмов (рыболовство, отдых), более значит-е пониж t. Схема. Топливо подают в потку парогенератора. Образуется пар в процессе сгорания, кот поступает в турбоагрерат (т/а) для выработки в электрогенераторе электроэнергии. После охлаждения в конденсаторе(К) отработанного в т/а пара его направляют в п/г для повт-го исп-я. Для охлаждения в К исп вода, кот подаётся из В-О с tзаб. Пройдя К, вода приобретает теплоту пара и выходит с более высокой tсб. Для охл-ся нужно 100-150 м3/с. \\\\ Тепловая нагрузка В-О – кол-во теплоты, поступающее с электростанции в В-О и приходящееся на 1 площади его поверхности. ТЭЦ будет работать норм, если tзаб не будет превыш предельно доп-ю (35С),а перепад дt между сб и заб не менее 8С. Чтобы охладить воду до дt=tсб-tзаб=8-10С, нужно иметь соотв площадь водохранилища Ω. В В-О есть циркуляционный (транзитный) поток, водоворотные и тупиковые области. Последние учит-ся коэфф-ми (Кэф). 1). Ωакт=Кэф Ω. Ωакт-активная площадь, т.е. кот принимает участие в охлаждении воды. \\\ Построение плана течений в нижнем бьефе ГЭС по закону расширения струи Бернадского b=b0(h0/h)exp(g(n2/hср4/3 –Ix/vср2)l), b0,h0,b,h-ширина и глубина транзитного (циркуляционного) потока (ТП) в нач и кон сечениях участка длиной l. n-коэф шероховатости, Ix-продольный уклон. Намечают ожидаему ось ТП (от водосброса к водозабору). Рассчитывают b1, на расстоянии l1. Повторяются расчёты для каждого очередного участка потока длиной li.Через концы полученных отрезков ширины bi проводят огибающие линии, кот явл границами ТП. \\\2). Оцениваем tзаб. Vx ɗt/ ɗx=λ/cρH ɗt/ɗz => ɗ t/ ɗw=∑Q/cρQц, где Qц-циркуляционный расход, w-уд площадь акт зоны В-О. \\\\ Градирня-устройства для охлаждения большого кол-ва воды направленным потоком атм воздуха. Брызгальный бассейн – с помощью трубопровода вода подаётся к водной поверхности; там разбрызгивается, охлаждаясь; затем, с водной поверхности, поступает для охлаждения объекта.
|
20. Расчёт температуры воды по длине реки. И
|
|
21. Метод теплового моделирования, его преимущества и недостатки. Вывод критерия Фурье. Метод теплового моделирования (ТМ) дает значительно большие возможности по сравнению с расчетными методами и при изучении нестационарных t-х полей, а также при изучении теплообмена в среде, являющейся теплоносителем. Чтобы тепловые процессы, протекающие на модели, были подобными таковым в натуре при ее изготовлении выполняются определенные требования. Эти требования сводятся к геометрическому, тепловому и механическому подобию натуры (Н) и модели (М) - равенству для них безразмерных критериев подобия. В теории теплового моделирования это критерии Фурье , Био, Грасгова и др. Геометрич подобие Н и М опр-ся соотнош-ми: хм=mlxн, yм=m1yн, zм=mlzн, [4] где xм и хн- линейные размеры М и Н, ml-масштаб модели, т.е. отношение линейных размеров М к соот линейным Н. Вывод критерия Фурье: Законы распространения теплоты как в Н, так и на М осуществляются в соответствии с уравнением теплопроводности: для натуры ɗtн/ɗτн=ɑн(ɗ2tн/ɗхн2+ɗ2tн/ɗун2+ɗ2tн/ɗzн2) [1]. Для модели : ɗtм/ɗτм =ɑм(ɗ2tм/ɗхм2+ɗ2tм/ɗум2+ɗ2tм/ɗzм2)[2], где их соотношение τм=mττн; ɑм=maɑн; tм=mttн [3]. τ –время протекания процесса, ɑ-коэф температуропроводн, mi-масштабные множители времени, коэф и t. Решим совместно [2],[3], [4]: ɗtн/ɗтн=mamt/ml2*ɑн(ɗ2tн/ɗх2н+ ɗ2tн/ɗу2н+ ɗ2tн/ɗz2н); Сравним с [1]: если множитель mamt/ml2=1 (это индикатор подобия) [5], то эти уравнения тождественны. Заменив в [5] значения масштабных множителей отношениями соответственных величин – [4], [3], получим: ɑτ/l2=Fо - критерий Фурье.=> выбор размера и материала модели д.б. подчинён требованиям Fo. Он позволяет опр-ть при заданных материале и размерах М, масштаб времени моделирования теплового процесса. t не влияет=> можно брать в произвольном диапазоне. На М д.б. осуществлены граничные условия, отвечающие Н. Если заданы граничн усл-я 3го рода, то нужно учесть: -λɗt/ɗn=ɑ(tп-tс). Сравниваем по аналогии: λм=mλλн, nм=ml nн, ɑм=mɑɑн, tп,м=mt tп,н, tс,м=mttс,н, Bi= ɑl/λ-критерий Био (когда не м.б. выполнены требования граничн усл 1го рода); критерий Пекле: Pe=vl/ʋ, ʋ-коэф кинематич вязкости, v-скорость потока; критерий Грасгофа: gβt дt l3/v2)=Gr, дt=tп-tc, βt-коэф объёмного расширения жидкости; критерий Архимеда: g (ρ-ρ0)/ ρ0 *l3/v2=Ar, ρ-пл жикости, ρ0 -окр среды. |
25. Зажорообразование и расчёт количества льда в зажоре. Зажор – скопление шуги с включением мелкобитого льда, вызывающее стеснение водного сечения и подъём уровня воды (зима). Кол-во шуги можно определить 1) бурением ледяного покрова и измерением толщины шуги под ним 2) по измеренным уровню и расходу воды на зажорном участке. 1-трудоёмкий+часто зажор обр-ся при небольшой толщите лед-го покрова=>не выйти на лёд. Рассм 2й способ. m заж=ρзаж ∑ (Fзажi li)\\\ ρзаж-плотность льда в зажоре, li – длина i-го участка между створами, n-число расчётных участков, mзаж –масса льда зажора, Fзаж – поперечное сечение зажора=Fобщ-Fжив. Расход воды под зажором: Qв=vFжив, v=Cкорень(HI) (Шези), С=1/n *H1/6 (Манинг), n-коэфф шероховатости, I-пьезометрич уклон.
|
|
22. Конвективные течения в водоёмах. Необходимость их учёта в гидротермических расчётах. Конвективные течения (КТ) (свободная конвекция) обусловлены распределением плотности жидкости (разницей плотности) как по вертикали, так и в плане, кот опр-ся t,S,P. При подогреве жидкости снизу нагретые частицы под действием плавучести поднимаются; более холодные=> в более тяжёлые частицы опускаются. Нагретые Ч, поднимаясь, перемешиваются с более холодными и постепенно охлаждаются за счёт теплопроводности. => их ρ увеличивается. Одновременно ρ поднимающейся жидкости ув-ся и за счёт диффузии. Возникшая конвекция може распространяться до свободн пов-ти жидкости или не дойти до неё, что зависит от исходного плотностного сост-я жидкости и степени нагрева придонных частиц. Активные струи ↑, реактивные ↓ \\\ (в практике) При охлаждении жидкости сверху конвективный процесс протекает в обратном порядке: охладившись, более тяжёлые частицы опускаются и вытесняют более лёгкие тёплые частицы. Может происх-ть по всей глубине, или погаситься на некоторой. Акт-↓, реакт- ↑. Max ρ при t=4C. Состояние воды описывается ура-ем ρ= ρ0(1-βt(t-t0)+βS(S-S0)), ρ0-равновесное значение плотности, кот соотв реперные значения t0, S0; βt, βS- коэф наблюдающихся в водоёмах суши t и S. Возникшие в водоёме плостностные КТ мб описаны с учётом этого ур-я, уравнениями Н-С, теплопроводности, диффузии. Они носят название системы ур-й Обербека-Буссинеска. \\\ Наблюдениями установлено, что плотностные КТ в водоёмах при отсутствии ветра и течений осущ-ся в форме ячеистой конвекции (ЯК): на пов-ти воды ЯК проявляется в виде 6-ти угольников. (ячейки Бенара). У периферии конв токи направлены ↓ –Реакт, а в центре ↑-Акт. Акт теплее=> ↑. При сильном ветре структура разрушается, при слабом-изменяется -циркуляция Ленгмюра. При ветре наблюдаются полосы пены, мелких предметов, пыли, льдин, кот расп-ся примерно на равных расст-ях друг от друга и направлены по ветру. \\\ Плотностная конвекция и ветровое перемешивание в стоячих водах явл причинами обра-я на некоторой глубине слоя t скачка и расслоения водных масс на три зоны: эпилимнион (верх), металимнион(ср-зона t скачка), гиполимнион (ниж застойная зона). Возникают КТ (рис.7.12). При охлаждении КТ от середины к берегам, при нагревании- наоборот. Придонные течения имеют обр-е напр-е. => КТ обусловлены разностью t воды в годизонт-м напр-ии. Поэтому утром к берегу приносит лодки, доски. Необходимость учёта: из-за КТ формируются зоны с повыш концентрацией солей и взвесий, что важно при отборе проб на мутность, хим.анализ.( в случае цирк-и Ленгмюра наиболее загр-я вода будет в области линий схождения). Из-за КТ проникают морские воды в устьевую зону реки по её дну (клин солёных вод). От этого зависит скоростной, термич и ледовый режимы реки.
|
24. Заторные и зажорные явления на реках. Методы борьбы с ними. Зажор – скопление шуги с включением мелкобитого льда, вызывающее стеснение водного сечения и подъём уровня воды (зима). Затор – скопление льдин в русле реки во время ледохода, вызывающее уменьшение водного сечения реки и подъём уровня воды (конец зимы и весна). Виды: 1 – образуется при подныривании льдин под кромку неподвижного ледяного покрова и отложнии их подо льдом; 2 – образуются у кромки сплошного ледяного покрова при скоплении ледяных масс (или др препядствия). Льдины, нагромождаясь, образуют голову, тело, хвост затора. При подъёме уровня воды в реке происходи отрыв ледяного покрова от берегов с образованием закраин. В оторвавшемся от берегов ЛП возникают напряжению, обусловленные трением воды о нижнюю пов-ть льда. В рез-те в ЛП происходит рост напряжений по его длине. Если в створе оно достигнет критич значения σкр=σв (временное сопр льда ЛП, соотв его прочности), то в этом створе и ниже по течению ЛП будет разрушаться, образуя ледяные поля и битый лёд. Активная сила Ра=Pn+2Pτ (ур-е равновесия сил, действ в заторе, тк силы в против-е стороны), сила трения Pτ=c+f Pб, с-сила сцепления, f-коэф трения раздробленного льда о берег, Рб-сила, действующ нормально к берегу со стороны раздр льда. \\\\\\ Они вызывают наводнения и разрушения заторным лъдом при его подвижках гидролошических сооружений: плотин, мостов, пирсов, водозаборов и др. Борьба с ними должна вестись с учётом природных особенностей реки и закономерностей процесса. 1. Предупредительные меры: а) возведение каскада или отдельных гидроузлов б) выравнивание русла в) взлом льда для прохода плывущего льда (ледоколом) г)бомбометание и подрывы льда (в Неве взрывать нельзя, тк по дну идёт кабель; можно поврелить набережные, мосты). д) искусственное усиление ледяного покрова путём удаления с него снега, намораживания льда 2. Непосредственная борьба при помощи ледоколов, подрывов, артобстрела, регулирования уровня воды (ув, чтобы поднялся затор и прошёл). Наибольший эффект будет достигнут, если ниже затора или зажора река будет освобождена ото льда или же в нём будет проделан широкий канал. 3. Заблаговременное предсказание места образования З и его мощности. Могут проводится ледокольные, взрывные, ледорезные и др работы или приняты соотв меры для изменения скоростного режима потока.
|
|
2
|
2 |
|
2 ɗξ/ɗт=1/(WρLкр)*(λм ɗt/ɗz|-0 -λт ɗt/ɗz|+0). Задачи о замерзании и оттаивании почв имеют решающее значение в вопросах прогноза весеннего стока.
|
28.
Методы расчёта испарения с поверхности
воды. МБ
исп-но несколько методов, тк сложный
механизм взаимодействия между водной
пов-ю (ВП) и прилегающей к ней воздушной
массой полностью не раскрыт. Более
точным считается инструментальный
(прямой) метод, т.е метод непосредственного
измерения слоя испарившейся воды с
помощью испарителей. К нему относится
и пульсационный метод. Но они не всегда
мб применены из-за их трудоёмкости и
невозможности исп-я при разработке
проекта. Поэтому применяют косвенные
методы. \\\Е-слой испарившейся воды,
мм/сут. \\\ Пульсционный.
Потоки воздуха почти всегда имеют
турбулентный характер движения.
Уравнение переноса водяного пара
нужно привести к виду, кот учитывает
этот хар-р движения. С помощью метода
осреднений (Рейнольдс) N= |
|
|
30. Определение испарения с водной поверхности с помощью испарителей. Зависимость величины испарения от площади испарителя. Погрешности измерения испарения. Наблюдение за испарением с помощью приборов регламентируются Наставлениями Госкомгидромета. Они уст методику, контроль и обработку рез-тов наблюдений. Наблюдения осущ на гидро станциях, расположенных в типичных природно-климатич зонах. Цель – изучение режима испарения. Более точные рез-ты об испарении с водн пов (ВП) можно получить, если приборы разместить на плавучих площадках (плотах). Но осущ сложно из-за плохой доступности. Поэтому наблюдения осущ по приборам, установл на береговой метеостанции, а рез-ты, с учётом коэфф, пересчитывают к значению измерений с водн пов-ти. В РФ создана сеть площадок, оборуд-х испарометром ГГИ-3000, эталонным водно-испарит бассейном S=20м2 глубиной 2м. Площадки, на кот осущ постановка спец тематических исследований, оснащаются бассейном 100м2. Испарение между сроками наблюдений по испарометку вычисляется как разность между уровнять воды в нём за предыдущ и текущ сроки наблюдений+слой осадков за период. Расчётное ур-е для перехода от показаний прибора к испарению с пов-ти водоёмов S до 1000 км2: Е= 0.43Е0.3 +0.9h+ -1.2дh+ +2.4τ -8.1дτ -35, E,E0.3-месячные норма испарения с ВП и испарометра ГГИ-3000, h+ -полуденная высота солнца, τ-прод-ть дня. Если есть сведения по бассейну (20), то расчёт водоёмов S до 40км2: Е=kнkзащβЕ20, kн-коэф, хар-щий влияние глубины водоёма на испарение, kзащ-коэф, хар-щий защищённость водоёма от ветра лесом, берегами, β-коэф, хар-щий влияние площади водоёма на испарение. \\\\\ В основе измерения испарения с водной пов-ти лежит ур-е водного баланса Е=Х±дН, Х-слой выпавших осадков за период измерения, дН- изменение уровня воды в испариетеле. Х измеряется с помощью дождемера. Пересчёт рез-тов измерения с ВП по испарит ГГИ-3000 на значения испарения с пов крупного водоёма осущ по той длинной формуле, либо Ефакт=RЕ3000, R=E20/Е300 – редукционный коэффициент. \\\ В комплект ГГИ-3000 входят: испаритель, дождемер, измерит трубка, объёмная бюретка, дождемерный стакан.
|
|
31. Акустические явления в воде. Ультразвук и его применение в гидрологии. А
|
32. Оптические свойства и явления в воде. Вода озёр, рек, водохр состоит из чистой воды, раствор-х веществ и взвесей. Оптические св-ва сильно зависят от этих составляющих. Состав раств-х в-в и взвесей (совокупность мелких частиц твердого вещества в жидкости или газе)- неорганические соли (Na,K,Mg,Cl,SO4) органич соединения (планктон, бактерии, пыльца), минеральные частицы и др. Часть видимых лучей солнечной радиации отражается от водной пов-ти в окр среду, а др часть, преломляясь, уходит в воду. Показатель преломления зависит от ρ среды. Альбедо – показатель отражательной способности. Естественный свет, распрострающ в воде, ослабляется по закону Багера-Ламберта Ez=E0 exp(-α z) (закон уменьшения звуковой энергии с глубиной). Ez-облучённость (освещённость) на глубине z, E0-облучённость прямо под пов-ю, α= χ+pσ-показатель вертикального ослабления облучённость (ослабление света), χ-показатель поглощения солнечн энергии, σ-пок-ль рассеяния солн энергии, р-коэф, хар состав воды. По закону Релея σ=32π3(n-1)2/(3λ4N), n-пок-ль преломления среды, N-число частиц в 1 см3, λ-длина волны света. Из закона известно, что осн влияние на рассеяние света в воде оказывает взвесь => σ убывает с глубиной. χ= χ0 exp(-μ0(λ-λ0)), χ0 –пок-ль поглощения при фиксированной длине волны λ0, μ0-коэф, зависящ от концентрации раствор-го вещ-ва. => χ зависит от концентрации раст в-ва и длины волны. С ростом концентрации в-ва χ ув-ся, с ростом длины уменьшается. Чем выше концентрация взвешанных частиц, тем сильнее поглощение уф-х и видимых лучей. Прозрачность воды – её св-во пропускать в глубь водоёма видимые лучи. Хаар-ки: 1) глубина видимости – глубина исчезновения белого диска «диска Секки». Диск d=0.3м, опущенный в воду. Наблюдение за глубиной видимости рекомендуется осущ с теневой стороны и в штиль, чтобы исключить влияние волнения воды и отражения исходящ и восходящ освещённости диска. 2) коэф прозрачности. Опр из закона Бугера-Ламберта. p=Iдz/I0=exp(-ε), Iz-поток излучения, прошедший через слой воды дz=1м; I0 -поток излучения, вошедший в этот слой, ε-показатель ослабления. Определение р и ε вып-ся с помощью приборов прозрачномеров на пробах воды. Цвет воды опр-ся цветом лучей, кот она рассеивает. Измерения желат-но при высоком стоянии Солнца и штиле. С ув-ем кол-ва взвеси и размеров её частиц вода зеленеет и приобретает желтоватый оттенок. Если взвеси нет-синий цвет. Если концентрация взвеси оч высокая, то вода приобр цвет этой взвеси. => по цвету воды можно опр происхождение воды. В горах синий, в тайге жёлто-коричневый. Шкала цветности (Форель, Уле)-набор пробиров с растворами мин-х солей. Сравнивая пробы воды со шкалой устанавл цвет. |
|
23=33. Электрические (магнитные) явления в почво-грунтах и воде, примеры их использования в практике. Омагниченная вода получается при пропускании её по трубопроводу, находящемуся в магнитном поле (МП). На неподвижную воду МП действует оч слабо. В 1945 Вермайер получил патент на способ борьбы с накипью в паровых котлах. Вода, пропущ через МП, не даёт накипи. Применяется на ТЭЦ, АЭС и др. С помощью такой воды бетон застывает быстрее и он прочнее, ув скорость протекания хим.реакций, ускорение прорастания семян и рост растений и др. Варианты, почему: 1)изменяется структура молекул воды; 2)влияют находящ в воде примиси. Точно не известно. \\\ Вода в ест водоёмах содержит ионы и различн взвешенные частицы, несущие заряд. Распределение их по акватории мб неодинаковым=>эл хар-ки могут значительно изменяться от места к месту. Электросмос. –движение жидкости через пористые материалы, обусловленное внешним эл.полем. проф Рейс. Эксперимент: U-образная трубка. Помещается пористый материал, напр, промытый песок, заливается водой. Слева Анод, справа Катод. После подачи напряжения к электродам, опущ в трубки, вода придёт в движение в направлении отрицат полюса (К). Справа уровень воды повысится. Электроосмос наблюд-ся при прохождении воды не только через песок, но и глину, грунт и др. Электрокинетический потенциал при электроосмосе ξ =4πμv1/(hD). μ-коэф вязкости, v-скорость, h=разность уровней воды, D-диэлектрич пост. Электрофорез –движение заряженных частиц, обусловленных внешним эл. полем. В кусов влажной глины вставлены 2 стеклянные трубки А и К. Насыпали на дно промытый песок, налили воды в них. Подали напряжение. Отрицат-но заряж частицы мигрировали к аноду. Внешне-помутнение воды (Ионы глины попали в воду). Уровень в А понизился, в К повысился. Электрический потенциал протекания – разность потенциалов, возникающ при протекании жидкости через пористую диафрагму (капилляр) под действием внешнего давления.уч Квинк. ЭДС пропорциональная давлению, под действием кот протекает жидкость. Явление, обратное электроосмосу. Потенциал тем выше, чем больше ионов диффузионного слоя выносится из капилляра в ед времени. Кол-во этих ионов пропорционально объёмой скорости жидкости и ξ-потенциалу: ξ=4πμU/(DP), U-разность потенциаов, возникающ на пов-ти диафрагмы, P-приложенное внешн давление. Электрический потенциал седиментации – разность потенциалов, возникающая между поверхностны и придонным слоями жидксти при быстром оседании тв-х частиц на дно. Обратно электрофорезу. Дорн. В ёмкость с неподвижной водой, к кот подлючены А и К, насыпаем песок. В рез-те движения возникает эл.ток, это видно на приборе для регистрации эл.тока. Двойной эл слой – 2 близких друг к другу слоя эл зарядов разного знака, но с одинаковой поверхностной ρ, возникающие на границе раздела 2х фаз. Это явление хар-но для рганица раздела 2х фаз различного хим состава, например, металла и раствора воды и воздуха (газовые пузырьки в воде). Пример капилляра, заполненного водой. В рез-те диссоциации пов-х молекул чстиц тв фазы капилляра на ионы происходит переход одного из них, напр, положит, в окр дисперсную среду (раствор). На пов-ти капилляра останется избыточное кол-во отрицат ионов. После того, как пов-ть тв фазы приобретёт эл зарят, она притянет к себе из раствора ионы отрицат знака в таком кол-.ве, что заряды компенсируются и образуется равновесный электронейтральный двойной эл слой. Т.е. будет избыток ионов +, во время нейтральности раствора вне этого слоя.
|
39. Зажоры, заторы, наледи, лавины – опасные явления природы. Методы борьбы с ними. Зажор – скопление шуги с включением мелкобитого льда, вызывающее стеснение водного сечения и подъём уровня воды (зима). Затор – скопление льдин в русле реки во время ледохода, вызывающее уменьшение водного сечения реки и подъём уровня воды (конец зимы и весна). Они вызывают наводнения и разрушения заторным лъдом при его подвижках гидролошических сооружений: плотин, мостов, пирсов, водозаборов и др. Борьба с ними должна вестись с учётом природных особенностей реки и закономерностей процесса. 1. Предупредительные меры: а) возведение каскада или отдельных гидроузлов б) выравнивание русла в) взлом льда для прохода плывущего льда (ледоколом) г)бомбометание и подрывы льда (в Неве взрывать нельзя, тк по дну идёт кабель; можно поврелить набережные, мосты). д) искусственное усиление ледяного покрова путём удаления с него снега, намораживания льда 2. Непосредственная борьба при помощи ледоколов, подрывов, артобстрела, регулирования уровня воды (ув, чтобы поднялся затор и прошёл). Наибольший эффект будет достигнут, если ниже затора или зажора река будет освобождена ото льда или же в нём будет проделан широкий канал. 3. Заблаговременное предсказание места образования З и его мощности. Могут проводится ледокольные, взрывные, ледорезные и др работы или приняты соотв меры для изменения скоростного режима потока. Наледь – многоструктурное образование на поверхности земли, льда или сооружения. Состоит из льда, линз воды, пузырьков воздуха и солей, выпадающих в осадок при замерзании. Толщина от мм до 2-3 м и более. Образуются от периодически изливаемой природной или техногенной воды. Это стихийное и опасное явление. При истечении воды или выпадении осадков происходит затопление большой территории и её увлажнение. Образовавшийся при замерзании этой воды лёд оказывает давление на сооружения (дамбы, авто и железнодороги, нефтепроводы, опоры), повышает скользкость дорог, аэродромов. Методы: 1. Пассивные: направлены на ликвидацию вредного воздействия наледей на хоз деят-ть чела без устранения причины их образования. Это сооружение дамб, заборов, сеток, преграждающих движение воды; применение способов искусственного таяния льда. 2. Активные: направлены на предотвращение наледообразования - промораживание/ теплоизоляция(утепляют и отводят по трубам) грунта, водотока; создание водонепроницаемых стенок; механич уборка снега и льда, покрытие пов-ти протиобмерзающими материалами. Лавина- масса снега, падающая или сползающая с горных склонов. В процессе движения лавина вовлекает новые массы снега на своем пути, поэтому ее масса нарастает к подножию. Причина- накопление снега на склонах гор, нарастание скатывающей силы, образование напряжений в снежном покрове, скачкообразное превышение скатывающей силы над силой сцепления. Обычно они возникают в рез-те интенсивного снегопада, повыш или пониж t воздуха, приложения разных внешних нагрузок. Иногда достаточно громкого звука (акустическая нагрузка). Поражающий фактор при сходе -кинетическая энергия снега, льда, вовлеченных предметов,и завалы. Плотность снега в лавине сильно возрастает и приближается к плотности бетона. При остановке лавины снег затвердевает с огромной скоростью и его можно только взрывать и пилить. Основная опасность - гибель оказавшихся на ее пути людей, разрушением авто- и железных дорог, ЛЭП, транспортных средств, зданий и сооружений. Способы уменьшения потерь: создание спец противолавинных служб, спасательных отрядов, закрытие районов на период повышенной опасности схода лавин. Используются спец инженерные защитные сооружения, способные направлять лавины в обход защищаемых мест. Применяется мониторинг и прогнозирование лавиноопасных участков. Организуются предупредительные спуски лавин путем обстрела лавиноопасных участков из артиллерийских орудий. |
|
35. Наледи, их форм(с?)ирование и разрушение. Наледь – многоструктурное образование на поверхности земли, льда или сооружения. Состоит из льда, линз воды, пузырьков воздуха и солей, выпадающих в осадок при замерзании. Толщина от мм до 2-3 м и более. Образуются от периодически изливаемой природной или техногенной воды. Условие образования: t пов-ти намерзания и воздуха<0, периодически поступающая вода на пов-ть. Классы: 1. Наледи подземных вод. Изливание воды, находящейся в почве под давлением (скважины, колодцы, шахты); свободная гравитационная разгрузка; воздействие криогенного (связ с низкими t) напора; 2.Н поверхностных вод. Поверхн-я вода изливается из-за: закупорки русла шугой, обильного снегопада (лёд прогибается), промерзания реки до дна, наводнений, приливов/отливов, ветрового нагона, периодического погружение ГС, сброс техногенной воды, поступление талой воды. 3. Н при растекании атмосферных вод. Выпадение жидких осадков (дождь, морось), конденсация водяных паров (?иней). Стадии замерзания: 1. Охлаждение воды до 0С. Для определения t воды и льда уравнение теплопроводности:ɗtв/ɗτ=ɑв ɗ2tв/ɗz2+W1/(cвρв)-для воды; для слоя льда вместо «в» «л». W-источник теплоты в толще воды (льда). Ещё условие Стефана. 2. Переохлаждения воды и зарождение кристаллов льда. После охлаждения до 0 будет процесс переохлаждения. Глубина зависит от состояния, в кот вода нах-ся и тепловой нагрузки. Образуется внутридонный лёд, кот всплывает на пов-ть и образует слой шуги 8-10 мм. Он, смерзаясь, предст собой корку льда. Процесс замерзания описывается уравнением: dQ=∑Qdτ; d(Lкр ρ hл) = (Qс+Qк+Qис+…)dτ => hл=1/(Lкр ρ) *(Qк+Qис)dτ (остальными Q пренебрегаем). 3. Рост толщины льда наледи. Дальнейший рост корки льда снизу из-за замерзания воды приводит к образованию наледи. Тк пов-ть имеет t<0, то замерзание и сверху и снизу. Мб ситуация, когда внутри останется незамёрзшая линза воды. При поступлении волны холода она замёрзнет. При этом произойдёт её расширение=> взрывное разрушение наледи. hл = -А+корень((A+hл0)2-(2 θ2 λл/(Lкр ρ))(τ-τ0)). \\\ А=λл/αсн+hсн λл/ λсн. Разрушение наледи. Обусловлено испарением наледи в рез-те вознонки (тв-газ), таянием, мех и хим воздействием на неё. Испарение происх под действ солнечной радиации, поступлением теплоты от подстил пов-ти. На пов-ти появляются чашеообразные углубления, образуется волнистый рельеф. Испарение неравномерно. Таяние начинается, когда верхний слой прогреется до 0С. Слой стаивания льда с пов-ти надели: hл=1/(Lпл ρ) ∑Q dτ \\\\ (Q-сумма тепловых потоков через пов-ть наледи). |
. |
|
34. Химический и электрический осмос. Явление мерзлотного выпучивания свай на водомерных постах. Мерзлотное пучение почвогрунтов (МППГ)связано с образованием в нём линз чистого льда, «сегрегационного льда». Плановые размеры и толщина линз опр грунтами, слагающими промерзаюущую толщу, их влажностью, глубиной промерзания. Обр линз и пучение нужно учиывать, тк МППГ приносит ущерб хоз деят-ти чела. Например, вспуч дороги. Весной, при оттаивании, грунт дороги сползает на стороны, после расстаивания самой линзы-образуется провалина. ТО, уменьшается прочность и надёжность дорог. Борьба-пропитка дорог хим растворами в целях упрочнения или засыпка под полотно дороги щебёнки или песка на глубину промерзаниц грунта (в них вода не зад-ся). Причина перемещения вды из обл с малым давлением в обл с высоким (P=ρм.г. hм.г.+ρлhл. ) – осмос. Хим.осмос – проникновение молекул раст-ля через полупроницаемую мембрану, разделяющую чистый раст-ль и раствор или 2 раствора различной концентрации. Развивающеемя в рез-те осмоса избыточное гидростатич давление измеряется столбом раствора высотой h, при кот устанавливается осмотич равновесие. Это осмотич давление. Оно мб вычислено по закону Вант-Гоффа: π=CRT, C=n/V (молярная конц р-ра), n-число молей неэлектролита, V-объём р-ра, R-универ газ пост, T-абс t. Если рассм почвогрунт как полупроницаемую мембрану с большой концентрацией солей в р-ре у его пов-ти в сравнении с нижерасположенными слоями, то можно обнаружить подъём воды к пов-ти и образование некоторого давления. \\\\ Вода в ест водоёмах содержит ионы и различн взвешенные частицы, несущие заряд. Распределение их по акватории мб неодинаковым=>эл хар-ки могут значительно изменяться от места к месту. Электросмос. –движение жидкости через пористые материалы, обусловленное внешним эл.полем. проф Рейс. Эксперимент: U-образная трубка. Помещается пористый материал, напр, промытый песок, заливается водой. Слева Анод, справа Катод. После подачи напряжения к электродам, опущ в трубки, вода придёт в движение в направлении отрицат полюса (К). Справа уровень воды повысится. Электроосмос наблюд-ся при прохождении воды не только через песок, но и глину, грунт и др. Электрокинетический потенциал при электроосмосе ξ =4πμv1/(hD). μ-коэф вязкости, v-скорость, h=разность уровней воды, D-диэлектрич пост. В
|
40. Определение прочностных характеристик льда. Изучение мех-х св-в ледяного покрова (ЛП) имеет важное значение для задач, таких как: сооружение ледяных переправ, защита ГЭС, портовых сооружений, мостов от разрушающего действия на них ЛП. Прочностные хар-ки оцениваются в лабораториях или в полевых условиях на образцах льда. Испытания произв-ят на спец машинах на сжатие, изгиб, растяжение, кручение, срез. К образцу прикладывают равномерно возрастающие статич нагрузки. По достижении нек-го критич её значения образец разрушается. Запас прочности сооружений, подвергающ воздействию ЛП, обосновывается max прочностью льда. 1 Сжатие. Лёд обладает упругопластичексими св-ми. 1)опр-е модуля деформации при кратковременной нагрузке 2)опр хар-ра связ деформаций с напряж-ями при медленном изменении нагрузки 3) опр временного сопротивления. Действующее напряжение сжатия: σсж=PS/F, S-площадь поршня пресса, F-площадь поперечн сечения образца, P-давление по маноментру с учётом поправок по паспорту. Относительная деформация εсж=дLсж/l0, l0-нач длина образца, дl-изменение дляны при нагрузке. Модуль деформации образца при сжатии Есж= σсж/εсж. Для испытания образца применяется гидравлич пресс. Образец 6х6х6 устанавливается на нижней площадке пресса. Закачивают масло в камеру=>площадка с образцом поднимается до упора в верхнюю площадку. Испытание при кратковременной нагрузке-для опр Eсж- масло закачивать нужно плавно, иначе разрушение произ-т быстро. Испытание при медленно изменении нагрузки-закачивать так, чтобы стрелка манометра останавливалась на опр отсчётах (25,50,75..) и не двигалась в теч 1 мин.В рез-те измерений строят графики (напряжение/отн деф-я). Угол наклона прямой позволяет опр Есж. 2.Изгиб осущ-ся на той же установке, с доп. приспособлениями. Подставка с 2мя опорными выступами снизу и выступом сверху, с помощью кот прикладывается нагрузка. Напряжение σизг=3LP/(2bh2), модуль деформации Eизг=((lP/(48Ifmax))(3L2-4l2), P-давление по манометру, L-расстояние между опорами, l-расстояние от опоры до точки приложения силы, b и h-ширина и высота образца, I=bh3/l2 – момент инерции попереч сечения, fmax –max прогиб балки. Посл-ть операций такая же. 3.Растяжение. на той же установке. Образец в виде восьмёрки с удлинённой шейкой. Он закладывается в спец приспособление, кот при сжатии площадками пресса приводят к растяжению образца. Формулы такие же, как при сжатии. Посл-ть операций тоже.
|
|
4
|
4 |
|
37. Влага в почвогрунтах и её передвижение. Почвогрунт (ПГ)– трёхфазная система, сост из почты, воды и воздуха, содержащего водяной пар. ПГ и снег-дисперсная система. Они отличаются от тв тел тем, что содержат поры. Оч мелкие поры-капиляры. Если поры ПГ полность заполнены водой-водонасыщение. Если нет-водоненасыщение. Зона ниже уровня грунтовых вод постоянно водонасыщенна. Слой почвы, непоср-но прилегающий к пов-ти грунтовых вод-капилярная зона (КЗ). Влажность почвы тут зависит от её высоты над пов-ю грунтовых вод. Выше КЗ-промежуточная зона, дальше-зона подвешенной (почвенной) влаги. Для описания передвижения влаги в водонасыщ почве применяют формулу Дарси: v=-kф ɗH/ɗx, kф – коэф фильтрации; Н-напор (градиент гидростатич давления (напора)), v-скорость фильтрационного потока. Коэф зависит от механич состава и структуры ПГ, вязкости жидкости. Водоненасыщение: влага передвигается при наличии градиентов влажности, t, плотности ПГ, концентрации хим р-ра и др, т.е. в одинаковых почвах наиболее интенсивное вижение влаги происходит из областей с более высокой влажностью или t в области с низкой вл-ю или t. Движение обусловлено климатическими условиями: осадками, t воздуха, Ра, солнечной радиацией и гидрологич факторами: глубиной залегания грунтовых вод, влагопроводностью и др. Массовая влажность (Wм)-массовая доля воды в 1 кг ПГ. Объёмная влажность (Wоб)-отношение объёма воды, нах-ся в порах, к объёма всего ПГ, в %. Объёмная пористость – объём пор в 1 м3 ПГ. Уравнение неразрывности влагопереноса: ɗWоб/ɗτ + ɗq/ɗn=0, τ-время, n-нормаль, вдоль кот проис-т движение влаги. Ф-потенциал почвенной влаги (работа, кот нужно совершить для удаления из почвы 1 кг воды). Ф=z+φк+ φс+ φосм+…, (z, φк..гравитац, капиллярный, сорбционный и осмотич потенциалы). Закон передвижения почвенной влаги: q=-k ɗФ/ɗn, k-коэф влагопроводности, q-поток влаги через ед сечения за ед времени; градиент общего потенциала. Решая совместно: уравнение влагопереноса в ПГ: ɗW/ɗτ=ɗ/ɗz (DW ɗW/ɗz)± ɗkz/ɗz, DW- коэф диффузии почв влаги, W=Wоб. \\\Аэрация – обмен почвенного поздуха с атмосферным, вентиляция почвы.
|
38. Проблемы, возникающие в устье реки после воздвижения плотины ГЭС. ГЭС - электростанция, в качестве источника энергии использующая энергию водного потока. 1. Каховская (Днепр, Украина). Солёная вода стала проникать из Ч.моря дальше в русло, поэтому население по берегам осталось без пресной воды, пропала пресноводная рыба. Решение:а) прокопать канал из другой реки, и пустить доп пресную воду. Отказались, тк долго копать б)построить плотину ниже Каховской СЭС, чтобы солёная вода не поступала. СССР распался, и идею не воплотили. 2. Красноярская. (Енисей, Карское море). а)При строительстве лес не вырубили, а затопили=> погибли животные, пропала древесина; б)животные не могут перебраться на др берег, звериные тропы перерезаны в)повысилась солёность и мутность воды (стала поступать вода из грунтов вечной мерзлоты, появились родники). г)решётки в ГЭС, защищающие от попадания крупного мусора, начали зарастать из-за бактерий д) в нижнем бьефе изменился t режим е) в Красноярске ув t воздуха в зимнее время, ум t в летнее ж) повысился уровень заболевания населения (бонхит, орви) из-за изменения климата. (После постройки ГЭС появилась незамерзающая полынья. Чтобы её уменьшить пытались, например, охлаждать искусственным снегом, но нужно слишком много снега; установить аэродинамические трубы, чтобы охлаждать воздух; пустить рядом приток через трубы чтобы охладить воду. Предполагалось, что полынья будет 20 км, оказалось 200 км. Климат стал более влажным из-за большего кол-ва незамерзающ воды зимой=> обмерзают провода, троллейбусы не ходят). Енисей в районе Красноярска перестал замерзать. Для решения можно построить контррегулятор, который обеспечит выравнивание расходов и уровней воды ниже створа контррегулятора, что позволит значительно уменьшить длину полыньи и создаст условия для образования ледяного покрова в нижнем бьефе и его сохранения на весь зимний период.
|
|
|
|
|
4. Формирование, рост и разрушение ледяного покрова. ЛП образуется в рез-те процессов теплообмена водоёмов с окр средой в осеннее-зимний период. При достижении 4С вода охлаждается с пов-ти без перемешивания на глубине. Дальнейшее охлаждение воды на пов-ти пр-дит до 0С, и даже до -1С (переохлаждённая). Чем спокойнее вода, тем на меньшую глубину проникает переохл-е. Там, где турбулентное перемешивание, мб по всей толщине воды. Переход в тв сост-е пр-дит при наличии в вое центров кристаллизации (взвешенные частицы в воде, кристаллы льда или снега из воздуха). Образует-ся сало. Чтобы кристаллы смёрзлись в монолитный ЛП, достаточно безветренной, ясной, морозной ночи. Бывает, что из-за небольшой глубины и отсутствия течений по берегам, установление ледостава начинается с берегов. (переохлаждение происх быстрее). В реках течения не позволяют в короткий срок образовать ЛП по всей пов-ти. Также ЛП может сформир-ся при замерзании шуги (рыхлые скопления льда, обр-ся из всплывшего на пов-ть внутриводного и донного льда, сала). Внутриводный лёд-кристаллы льда, нах-ся по всей толщине переохл-й воды, донный-скопление (примерзание) внутриводного на дне или предметах в воде. Продолжительность формирования ЛП определяется соотношением между теплоотдачей с водной поверхности и интенсивностью турбулентного перемешивания водных масс. Разновидности льда: 1. Водный (кристаллический) лед, образовавшийся из чистой воды при спокойном ее состоянии с ориентацией оси кристалла к поверхности воды. В весенний период от проникающей в лед солнечной радиации таяние льда начнется прежде всего на гранях кристаллов между этих прослоек, т.е. температура плавления льда здесь ниже. 2. Шуговой лед, образовавшийся при замерзании всплывшей на поверхность шуги, представляющей собой кристаллы льда с различной ориентацией осей. Он может быть не сплошным и включенным в водный лед, а также многослойным. Он обычно содержит пузырьки воздуха и взвешенные наносы, менее прозрачен, чем водный лед. По этой причине внутриледное таяние его в весенний период более интенсивное, чем кристаллического льда. 3. Снеговой лед, образовавшийся в результате замерзания пропитанного водой снега на льду. Такой лед, как и шуговой, непрозрачен из-за большого количества пузырьков воздуха, он подвержен по этой причине интенсивному внутрикристаллическому таянию в весенний период. 4. Наледный лед, образовавшийся в результате замерзания воды растекающейся по ледяному покрову, представляет собой слоистую структуру, непрозрачен. Разрушение Процесс вскрытия водоемов и водотоков различен по прод-ти и опр-ся тепловыми (солнечная радиация (СР), приход тёплых воздушных масс, поступление по реке тёплых водных масс) и механическими факторами (течение воды под ЛП, ветер, подъем уровня воды). 1.Тепловые факторы. Процессу таяния льда ЛП предшествует таяние снега, его покрывающего. После его стаивания происходит таяние льда как с верхней поверхности ЛП (обусл-ое СР и турбулентным теплообменом с атмосферой), так и с нижней поверхности (обусл-ое теплыми водами, прогретыми проникающей СР через лед, или водами, пришедшими из других районов). Одновременно происходит прогревание и таяние льда по всей его толще, обусловленное поглощением СР. Наличие во льду примесей увеличивает его поглощат-ю способность по отнош к СР, что сказывается на интенсивности его таяния и ослаблении связей между кристаллами льда. В результате сплошность ледяной массы нарушается и распадается на ряд зерен и столбчатых кристаллов. 2.Механические факторы. Таяние снега, лежащего на водосборе и на льду реки, приводит к повышению уровня воды в реке и отрыву ледяного покрова от берегов. На оторвавшийся от берегов ЛП по нижней его поверхности действует касательная сила, обусловленная течением водного потока. Она вызывает в нем напряжения, которые могут превзойти напряжения, опр-е прочность льда, произойдет его разрушение на отдельные поля. Эти поля при столкновении с берегами и друг с другом разламываются на льдины и начинается ледоход. Если разрушение ЛП происходит и в начале его таяния, то фактором является интенсивный подъем уровня воды, вызванный приходом паводочной волны. Действие ветра при разрушении ЛП аналогично действию водного потока на него: оно сказывается на озерах и водохранилищах. Важно также волнение воды, вызванное ветром. Прод-ть ледохода на реках зависит от толщины льда, его степени раздробленности, размеров реки и климатических условий. \\\ При разрушении ЛП на озерах и водохранилищ ах доминирующими факторами являются тепловые, мех только довершают этот процесс. В речных потоках, наоборот, мех факторы, воздействующие на него, превалируют над тепловыми. P=ɑv2 -течение с нижней пов-ти льда. Рост hл = -А+корень((A+hл0)2-(2 θ2 λл/(Lкр ρ))(τ-τ0)). \\\ А=λл/αсн+hсн λл/ λсн. hл =φ(∑θ2)n-сумма средних суточных знач t, фи и n-эмперич коэф-ты. Рост зависит от можности и плотности снежного покрова, погодных условий (Ветер штиль), теплопотока из водноё массы, интенсивности потока лучистого тепла. |
13. Методы решения уравнений стационарной теплопроводности: аналитический, графический, релаксаций. 15. Метод графоаналитического интегрирования уравнения теплопроводности для двухмерного стационарного температурного поля. АМ состоит в том, что пользуясь полной математич формулировкой задачи, находят её аналитич решение. Следует искать готовое решение, а не новое. Если нет готового-сумма др готовых (с помощью принципа суперпозиции). «+» точность решений, зависит лишь от точности закладываемых в условие данных. t рассчитывается для любой точки тела и для любого момента времени. «-»-ограниченность круга задач. М Метод релаксации. М Получаем t 1+t 2 +t 3 +t 4-4t0=0. Если она не находится в равновесии с соседними значениями температуры, то правая часть этого уравнения не будет равна нулю, т. е. 1+t 2 +t 3 +t 4-4t0 =дt. Где дt=0. Затем вычислим в этих точках остаток дt. Полученный остаток говорит о том, что температура льда в этих точках принята неправильно. ее необходимо выровнять методом последовательного приближения, начиная с точки, в которой наблюдается максимальный остаток. Таким образом, метод релаксации заключается в том, что, задаваясь первоначально произвольным, но более или менее вероятным распределением температуры, затем постепенно выравнивают ее последовательным приближением, пользуясь уравнениями которые выше.
|

 лотность
одн среды определяется массой вещества
среды в единице объёма (p=m/V).
p=f(t,
S
(солёность), P
(давл)) (опр.экспериментально). p
изменяется с изм t
незначительно, поэтому в практич
расчётах принимается 1000 кг/м3.(наиб p
при t=4C).
ρ
солёной воды (зав от S)
> ρ
дистиллированной. Пресная вода –
S<0.5‰.
S<24,7
– солоноватая, 24,7-40 – солёная, S>40
– сильно солёная вода. Сжимаемость
хар-ся
коэфф сжимаемости бета В=относительное
изменение объёма/изменение давления.
В= - dV/V*1/dP.
B=
- дV/V
*1/дP.
Минус показывает, что увеличению P
соотв-ет уменьшение V.
Модуль объёмной упругости (объёмного
сжатия) k=1/B.
Если произвести расчёты, то вода очень
мало сжимаема. (дельтаV=5*10^-3
м3). B
уменьшается при повыш t,S,P.
Вода расшир при пов t
и сжим при пониж-и. Коэф объёмного
расширения = относительное изменение
объёма жидкости/ изменение t.
Bt=
dV/V*1/dt.
Bt=
дV/V
*1/дельта t.
Температура
наибольшей плотности
при норм P=1,01*10^5
равна 3.98 C
(4). Темп кристаллизации дистил воды
при н.а.д. принимается равной 0С. При
замерзании воды д.б. переохлаждённой
(порядка -1С), тк при 0С равновесие фаз.
Теплофизические
хар-ки воды. Теплоёмкость
– кол-во теплоты, поглощаемой телом
при нагревании на 1С. C=Q/дt.
Характеристика теплоёмкости вещ-ва
удельная
теплоёмкость
- колв-о теплоты, необходимое для
нагревания 1 кг дист воды на 1С. Она
слабо зависит от t
и в практич расчётах равна с=4,2
кДж/(кг*град). c=Q/(mдt).
Удельная теплота кристаллизации
Lкр
– количество теплоты, которое выделяется
при кристаллизации 1 кг воды при пост
t.
Lкр=Qкр/m,
Lпл=Qпл/m=33,5*10^4
Дж/кг(для дист). Удельная теплота
испарения (обратное – конденсации)
Lи
– кол-во теплоты, необходимое, чтобы
перевести 1 кг воды в парообразное
состояние при пост температуре.
Lи=Qи/m=25*10^5
Дж/кг (при 0С) , Lк=Qк/m.
Температуропроводность
– физ параметр вещества, характеризующий
скорость выравнивания температуры в
различных точках тела. Коэфф темппроводн
альфа=λ/(cp).
λ-коэф теплопроводности. Вязкость
Объёмная – способность жидкости
воспринимать растягивающие усилия
(при распространении звуковых и
ультразвуковых волн). Тангенциальная
вязкость
– способность жидкости оказывать
сопротивление сдвигающим усилиям.
Силы внутреннего трения пропорциональны
градиенту скорости по нормали и
площади, на которую они действуют.
Относя силу внутр трения к площади
(=1), получаем касательное напряжение
в жидкости τ=μ *ɗv/ɗn,
μ-динамич коэф вязкости (опр силу
трения на единицу поверхности при
град=1). Зависит от t.
Поверхностное
натяжение.
Возникает на поверхности соприкасания
воды с воздухом, тв телом или др
жидкостью. Обусловлено силами притяжения
между молекулами в этих телах. ПН
стремится уменьшить поверхность
жидкости до min.
Поэтому капли имеют сферич форму. Сила
ПН действует на свободной пов-ти капли.
Направлена по касательное к пов-ти и
нормально к границе свободн пов-ти.
F=σl,
l-длина
контура пов-ти жидкости, σ-коэфф
ПН (Н/м). Смачивание.
При соприкосновении тв тела с водой
смачивание наблюдается тогда, когда
взаимодействие между их молекулами
сильнее взаимодействия между молекулами
самой воды. Вода будет стремится ув
пов-ть соприкосновения и растечётся
по тв телу. И наоборот. Поверхность
смачивающей жидкости в узких капиллярах
принимает вогнутую форму. При вогнутом
мениске давление воды под ним меньше
атмосферного на уровне горизонта
подземных вод Pа
на величину дР=2σ/r,
r-радиус
кривизны мениска. дР= ρgh,
h-высота
уровня воды в капилляре. Электрические
свойства воды
Удельное эл сопротивление ρэ зависит
от t.
Диэлектрическая проницаемость ε
показывает, во сколько раз напряжённость
поля с данным веществом ниже, чем в
вакууме. При 20С, ε=81. Тяжёлая вода. В
природных водах суши есть в оч слабых
концентрациях 1:7000. В состав входит
тяжёлый изотоп водорода 2Н (2 сверху),
кот наз-ся дейтерий. Формула тяж
воды-D20.
t
кр=3,82С, tкип=11,6С.
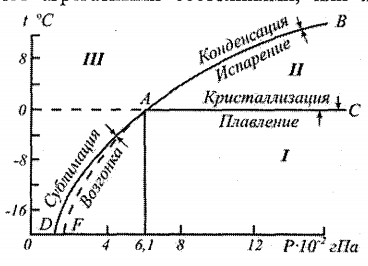
Плотность при 20С=1105,6. Переход из одной
фазы в другую обусловлен изменением
t,P.
I
– тв, II-
ж, III
–пар. Вдоль линии АС вода нах-ся в
состоянии равновесия между тв и ж
фазами. Вдоль АВ – между ж и газ, вдоль
АD
– тв и газ. Равновесие фаз вдоль АВ,
АС, АD,
надо понимать как динамическое
равновесие, те вдоль этих кривых число
вновь образующихся молекул 1 фазы
равно числу в.о.м. др фазы. АС – кривая
зав-ти t
плавления от Р, АВ-t
кип от Р, АD
– Р пара тв фазы от t.
Точка А – тройная точка (Р=610,6 Па,
t=0.01C).
Переход из тв в газ – возгонка, из газ
в тв- сублимация. Кривые описываются
уравнением Клапейрона-Клаузиуса
dP/dT=L/T
(V2-V1).
лотность
одн среды определяется массой вещества
среды в единице объёма (p=m/V).
p=f(t,
S
(солёность), P
(давл)) (опр.экспериментально). p
изменяется с изм t
незначительно, поэтому в практич
расчётах принимается 1000 кг/м3.(наиб p
при t=4C).
ρ
солёной воды (зав от S)
> ρ
дистиллированной. Пресная вода –
S<0.5‰.
S<24,7
– солоноватая, 24,7-40 – солёная, S>40
– сильно солёная вода. Сжимаемость
хар-ся
коэфф сжимаемости бета В=относительное
изменение объёма/изменение давления.
В= - dV/V*1/dP.
B=
- дV/V
*1/дP.
Минус показывает, что увеличению P
соотв-ет уменьшение V.
Модуль объёмной упругости (объёмного
сжатия) k=1/B.
Если произвести расчёты, то вода очень
мало сжимаема. (дельтаV=5*10^-3
м3). B
уменьшается при повыш t,S,P.
Вода расшир при пов t
и сжим при пониж-и. Коэф объёмного
расширения = относительное изменение
объёма жидкости/ изменение t.
Bt=
dV/V*1/dt.
Bt=
дV/V
*1/дельта t.
Температура
наибольшей плотности
при норм P=1,01*10^5
равна 3.98 C
(4). Темп кристаллизации дистил воды
при н.а.д. принимается равной 0С. При
замерзании воды д.б. переохлаждённой
(порядка -1С), тк при 0С равновесие фаз.
Теплофизические
хар-ки воды. Теплоёмкость
– кол-во теплоты, поглощаемой телом
при нагревании на 1С. C=Q/дt.
Характеристика теплоёмкости вещ-ва
удельная
теплоёмкость
- колв-о теплоты, необходимое для
нагревания 1 кг дист воды на 1С. Она
слабо зависит от t
и в практич расчётах равна с=4,2
кДж/(кг*град). c=Q/(mдt).
Удельная теплота кристаллизации
Lкр
– количество теплоты, которое выделяется
при кристаллизации 1 кг воды при пост
t.
Lкр=Qкр/m,
Lпл=Qпл/m=33,5*10^4
Дж/кг(для дист). Удельная теплота
испарения (обратное – конденсации)
Lи
– кол-во теплоты, необходимое, чтобы
перевести 1 кг воды в парообразное
состояние при пост температуре.
Lи=Qи/m=25*10^5
Дж/кг (при 0С) , Lк=Qк/m.
Температуропроводность
– физ параметр вещества, характеризующий
скорость выравнивания температуры в
различных точках тела. Коэфф темппроводн
альфа=λ/(cp).
λ-коэф теплопроводности. Вязкость
Объёмная – способность жидкости
воспринимать растягивающие усилия
(при распространении звуковых и
ультразвуковых волн). Тангенциальная
вязкость
– способность жидкости оказывать
сопротивление сдвигающим усилиям.
Силы внутреннего трения пропорциональны
градиенту скорости по нормали и
площади, на которую они действуют.
Относя силу внутр трения к площади
(=1), получаем касательное напряжение
в жидкости τ=μ *ɗv/ɗn,
μ-динамич коэф вязкости (опр силу
трения на единицу поверхности при
град=1). Зависит от t.
Поверхностное
натяжение.
Возникает на поверхности соприкасания
воды с воздухом, тв телом или др
жидкостью. Обусловлено силами притяжения
между молекулами в этих телах. ПН
стремится уменьшить поверхность
жидкости до min.
Поэтому капли имеют сферич форму. Сила
ПН действует на свободной пов-ти капли.
Направлена по касательное к пов-ти и
нормально к границе свободн пов-ти.
F=σl,
l-длина
контура пов-ти жидкости, σ-коэфф
ПН (Н/м). Смачивание.
При соприкосновении тв тела с водой
смачивание наблюдается тогда, когда
взаимодействие между их молекулами
сильнее взаимодействия между молекулами
самой воды. Вода будет стремится ув
пов-ть соприкосновения и растечётся
по тв телу. И наоборот. Поверхность
смачивающей жидкости в узких капиллярах
принимает вогнутую форму. При вогнутом
мениске давление воды под ним меньше
атмосферного на уровне горизонта
подземных вод Pа
на величину дР=2σ/r,
r-радиус
кривизны мениска. дР= ρgh,
h-высота
уровня воды в капилляре. Электрические
свойства воды
Удельное эл сопротивление ρэ зависит
от t.
Диэлектрическая проницаемость ε
показывает, во сколько раз напряжённость
поля с данным веществом ниже, чем в
вакууме. При 20С, ε=81. Тяжёлая вода. В
природных водах суши есть в оч слабых
концентрациях 1:7000. В состав входит
тяжёлый изотоп водорода 2Н (2 сверху),
кот наз-ся дейтерий. Формула тяж
воды-D20.
t
кр=3,82С, tкип=11,6С.
Плотность при 20С=1105,6. Переход из одной
фазы в другую обусловлен изменением
t,P.
I
– тв, II-
ж, III
–пар. Вдоль линии АС вода нах-ся в
состоянии равновесия между тв и ж
фазами. Вдоль АВ – между ж и газ, вдоль
АD
– тв и газ. Равновесие фаз вдоль АВ,
АС, АD,
надо понимать как динамическое
равновесие, те вдоль этих кривых число
вновь образующихся молекул 1 фазы
равно числу в.о.м. др фазы. АС – кривая
зав-ти t
плавления от Р, АВ-t
кип от Р, АD
– Р пара тв фазы от t.
Точка А – тройная точка (Р=610,6 Па,
t=0.01C).
Переход из тв в газ – возгонка, из газ
в тв- сублимация. Кривые описываются
уравнением Клапейрона-Клаузиуса
dP/dT=L/T
(V2-V1).
 .
Ледяной покров рек, озёр и водохранилищ
и расчёт его толщины. Важность знания
этой характеристики.
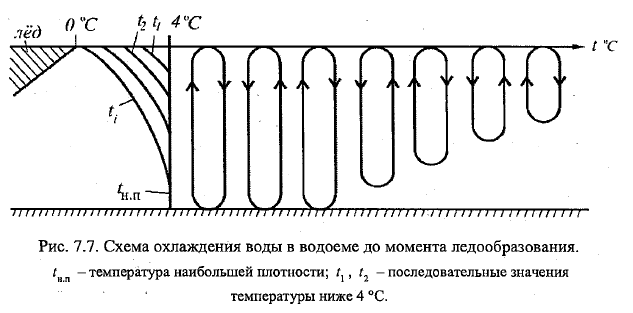
ЛП образуется в рез-те процессов
теплообмена водоёмов с окр средой в
осеннее-зимний период. При достижении
4С вода охлаждается с пов-ти без
перемешивания на глубине. Дальнейшее
охлаждение воды на пов-ти пр-дит до
0С, и даже до -1С (переохлаждённая). Чем
спокойнее вода, тем на меньшую глубину
проникает переохл-е. Там, где турбулентное
перемешивание, мб по всей толщине
воды. Переход в тв сост-е пр-дит при
наличии в вое центров кристаллизации
(взвешенные частицы в воде, кристаллы
льда или снега из воздуха). Образует-ся
сало. Чтобы кристаллы смёрзлись в
монолитный ЛП, достаточно безветренной,
ясной, морозной ночи. Бывает, что из-за
небольшой глубины и отсутствия течений
по берегам, установление ледостава
начинается с берегов. (переохлаждение
происх быстрее). В реках течения не
позволяют в короткий срок образовать
ЛП по всей пов-ти. Также ЛП может
сформир-ся при замерзании шуги (рыхлые
скопления льда, обр-ся из всплывшего
на пов-ть внутриводного и донного
льда, сала). Внутриводный
лёд-кристаллы
льда, нах-ся по всей толщине переохл-й
воды, донный-скопление
(примерзание) внутриводного на дне
или предметах в воде (примерзает, т.к.
у металла др теплопроводность, происх-т
передача тепла и примерзание). hл=φ(∑θ2)n
, в
скобках-сумма (от 0 до τ
-за период образования ледостава)
среднесуточных t
воздуха, φ,n-эмпирич
коэф. Дата начала ледостава-первый
день образования неподвижного ЛП. Эта
формула не учит мощность плотность
СП, погодные условия, потока солнечного
тепла и др. Lкр
ρ dhл/dτ=∑Q,
∑Q=QR+QK+…,
слагаемыми пренебрегают, т.к. они
взаимно компенсируют друг друга, и в
итоге Lкр
ρ
dhл/dτ=Qк=ɑ(tп-θ2),
ɑ-коэф теплоотдачи от пов-ти снега к
воздуху=>hл
= -А+корень((A+hл0)2-(2
θ2
λл/(Lкр
ρ))(τ-τ0)).
\\\ А=λл/αсн+hсн
λл/
λсн.
\\\ Значение
толщины льда важно
для расчёта нагрузки (статистич и
динамич давления) на ГС, мосты, причалы,
для расчёта количества льда в заторе,
размеров навалов льда и др.
.
Ледяной покров рек, озёр и водохранилищ
и расчёт его толщины. Важность знания
этой характеристики.
ЛП образуется в рез-те процессов
теплообмена водоёмов с окр средой в
осеннее-зимний период. При достижении
4С вода охлаждается с пов-ти без
перемешивания на глубине. Дальнейшее
охлаждение воды на пов-ти пр-дит до
0С, и даже до -1С (переохлаждённая). Чем
спокойнее вода, тем на меньшую глубину
проникает переохл-е. Там, где турбулентное
перемешивание, мб по всей толщине
воды. Переход в тв сост-е пр-дит при
наличии в вое центров кристаллизации
(взвешенные частицы в воде, кристаллы
льда или снега из воздуха). Образует-ся
сало. Чтобы кристаллы смёрзлись в
монолитный ЛП, достаточно безветренной,
ясной, морозной ночи. Бывает, что из-за
небольшой глубины и отсутствия течений
по берегам, установление ледостава
начинается с берегов. (переохлаждение
происх быстрее). В реках течения не
позволяют в короткий срок образовать
ЛП по всей пов-ти. Также ЛП может
сформир-ся при замерзании шуги (рыхлые
скопления льда, обр-ся из всплывшего
на пов-ть внутриводного и донного
льда, сала). Внутриводный
лёд-кристаллы
льда, нах-ся по всей толщине переохл-й
воды, донный-скопление
(примерзание) внутриводного на дне
или предметах в воде (примерзает, т.к.
у металла др теплопроводность, происх-т
передача тепла и примерзание). hл=φ(∑θ2)n
, в
скобках-сумма (от 0 до τ
-за период образования ледостава)
среднесуточных t
воздуха, φ,n-эмпирич
коэф. Дата начала ледостава-первый
день образования неподвижного ЛП. Эта
формула не учит мощность плотность
СП, погодные условия, потока солнечного
тепла и др. Lкр
ρ dhл/dτ=∑Q,
∑Q=QR+QK+…,
слагаемыми пренебрегают, т.к. они
взаимно компенсируют друг друга, и в
итоге Lкр
ρ
dhл/dτ=Qк=ɑ(tп-θ2),
ɑ-коэф теплоотдачи от пов-ти снега к
воздуху=>hл
= -А+корень((A+hл0)2-(2
θ2
λл/(Lкр
ρ))(τ-τ0)).
\\\ А=λл/αсн+hсн
λл/
λсн.
\\\ Значение
толщины льда важно
для расчёта нагрузки (статистич и
динамич давления) на ГС, мосты, причалы,
для расчёта количества льда в заторе,
размеров навалов льда и др.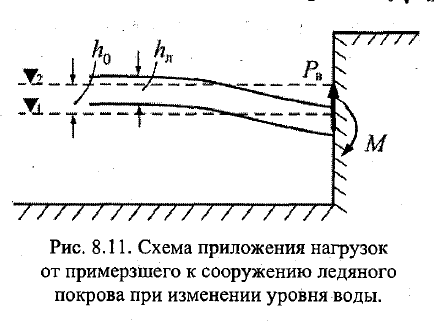 агрузки,
обусловленные кинетической энергией
движущегося льда, называются
динамическими
нагрузками (ДН).
ДН льда на ГС зависят от прочностных
характеристик и характера взаимодействия
лед. Поля с сооружением. Предусматривают
расчет следующих ДН: 1)от движущихся
ледяных полей на сооружение с
вертикальной передней гранью: для
отдельно стоящих опор при прорезании
ими льда ; для отдельно стоящих опор
при остановке ледяного поля опорой
;для секции сооружения при ударе
отдельных льдин ; для секции сооружения
при разрешении льда. 2) от ЛП на сооружение
откосного профиля или на отдельно
стоящую опору , имеющую в зоне действия
льда наклонную поверхность. 3) от
движущихся ЛП на сооружение из ряда
вертикальных опор. 4)от остановившегося
ЛП , наваливающегося на сооружения
под воздействием течения воды и ветра.
5) при прорезании опорой зажорной массы
льда. 6) при навале зажорной массы льда
на сооружении перпендикулярно его
фронту. 7)от навала зажорных масс льда
на единицу длины сооружения,
расположенного параллельно направлению
течения, а также на берега. \\\ Максимальная
нагрузка на опору при прорезании ею
,льдины может определена по формуле
P=mjQpbhл
,где
mj-коэф.формы
опоры. Если ЛП остановится , то формула
такова P=0,4vлhл(mEΩQp)1/2
, где mE-
коэф.формы опоры, Ω-площадь
ЛП.
агрузки,
обусловленные кинетической энергией
движущегося льда, называются
динамическими
нагрузками (ДН).
ДН льда на ГС зависят от прочностных
характеристик и характера взаимодействия
лед. Поля с сооружением. Предусматривают
расчет следующих ДН: 1)от движущихся
ледяных полей на сооружение с
вертикальной передней гранью: для
отдельно стоящих опор при прорезании
ими льда ; для отдельно стоящих опор
при остановке ледяного поля опорой
;для секции сооружения при ударе
отдельных льдин ; для секции сооружения
при разрешении льда. 2) от ЛП на сооружение
откосного профиля или на отдельно
стоящую опору , имеющую в зоне действия
льда наклонную поверхность. 3) от
движущихся ЛП на сооружение из ряда
вертикальных опор. 4)от остановившегося
ЛП , наваливающегося на сооружения
под воздействием течения воды и ветра.
5) при прорезании опорой зажорной массы
льда. 6) при навале зажорной массы льда
на сооружении перпендикулярно его
фронту. 7)от навала зажорных масс льда
на единицу длины сооружения,
расположенного параллельно направлению
течения, а также на берега. \\\ Максимальная
нагрузка на опору при прорезании ею
,льдины может определена по формуле
P=mjQpbhл
,где
mj-коэф.формы
опоры. Если ЛП остановится , то формула
такова P=0,4vлhл(mEΩQp)1/2
, где mE-
коэф.формы опоры, Ω-площадь
ЛП.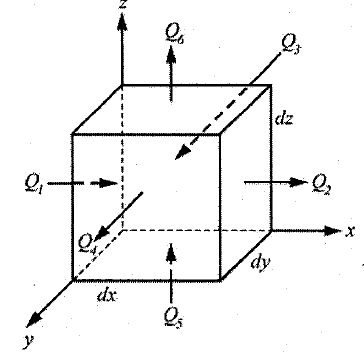 писывает
нестационарное пространственное t-е
поле, т.е. где значения t
меняются в каждой точке во времени.
Выделим в однородном тв теле объём V
в системе декартовых координат (xyz),
основные координаты совместим с
гранями dx,dy,dz.
В пределах V,
t меняется в 3ч направлениях. => через
3 грани в направлении 3х осей будут
входить кол-во теплоты Q1,Q3,Q5;
через 3 противоположн грани будет
выходить кол-во теплоты Q2,Q4,Q6.
ЗСЭ: кол-во теплоты, поступающее в V
через его грани за время t
равно изменению энтальпии этого V–Q7.
∑Q=Q7.
По формуле Q=qF
(q-уд
тепловой поток): Q1=qx
dxdydz,
Q3=qy
dxdydz;
Q2=
- (qx+(ɗqx/ɗx)dx)dxdydz;
Q4=-
(qy+(ɗqy/ɗy)dy)dxdydz;
Q7=cρ
dxdydz
ɗt/ɗτ
dτ.
(qi-
уд тепловые потоки через грани соотв
х, у, z;
dqi/
d x ,-
изменение уд тепловых потоков внутри
выделенного
объема по
осям х, у, z;
dt/dx —
изменение
температуры этого объема за время
dx). Решая
совместно и деля на dxdydz
dτ,
cρ:
ɗt/ɗτ=
-1/cρ
(ɗqx/ɗx+
ɗqy/ɗy+ɗqz/ɗz);
По з.Фурье: q=
-λ ɗt/ɗn
(λ-коэф пропорц) => ɗt/ɗτ=
λ/cρ
(ɗ2t/ɗx2+
ɗ2t/ɗy2+ɗ2t/ɗz2);
Обозначив скобище за▼(оператор
Лапласа), и λ/cρ=a
(коэф температуропр-ти) => ɗt/ɗτ=a▼2t.
Можно записать в цилиндрич координатах
(x=rcosφ,
y=rsinφ,
z=z):
ɗt/ɗτ=a(ɗ2t/ɗr2+1/r
*ɗt/ɗr+1/r2
*ɗ2t/ɗφ2+ɗ2t/ɗz2);
Для нестационарного двухмерного t
поля: ɗt/ɗτ=
a(ɗ2t/ɗx2+
ɗ2t/ɗy2);
Для нестац-го одномерного: ɗt/ɗτ=
a(ɗ2t/ɗx2).
Стац
поле-это
поле, в кот t’=f(x,y,z)=const.
Если t=const=>левая
часть всех ур-й=0, «а» отбрасываем и
записываем 3 ур-я. \\\ Ур-е с ▼ позволяет
решить задачу, когда нет источников
теплоты. Если есть, то к правой части
прибавляем W/cρ,
(W-интенсивность
источника).
писывает
нестационарное пространственное t-е
поле, т.е. где значения t
меняются в каждой точке во времени.
Выделим в однородном тв теле объём V
в системе декартовых координат (xyz),
основные координаты совместим с
гранями dx,dy,dz.
В пределах V,
t меняется в 3ч направлениях. => через
3 грани в направлении 3х осей будут
входить кол-во теплоты Q1,Q3,Q5;
через 3 противоположн грани будет
выходить кол-во теплоты Q2,Q4,Q6.
ЗСЭ: кол-во теплоты, поступающее в V
через его грани за время t
равно изменению энтальпии этого V–Q7.
∑Q=Q7.
По формуле Q=qF
(q-уд
тепловой поток): Q1=qx
dxdydz,
Q3=qy
dxdydz;
Q2=
- (qx+(ɗqx/ɗx)dx)dxdydz;
Q4=-
(qy+(ɗqy/ɗy)dy)dxdydz;
Q7=cρ
dxdydz
ɗt/ɗτ
dτ.
(qi-
уд тепловые потоки через грани соотв
х, у, z;
dqi/
d x ,-
изменение уд тепловых потоков внутри
выделенного
объема по
осям х, у, z;
dt/dx —
изменение
температуры этого объема за время
dx). Решая
совместно и деля на dxdydz
dτ,
cρ:
ɗt/ɗτ=
-1/cρ
(ɗqx/ɗx+
ɗqy/ɗy+ɗqz/ɗz);
По з.Фурье: q=
-λ ɗt/ɗn
(λ-коэф пропорц) => ɗt/ɗτ=
λ/cρ
(ɗ2t/ɗx2+
ɗ2t/ɗy2+ɗ2t/ɗz2);
Обозначив скобище за▼(оператор
Лапласа), и λ/cρ=a
(коэф температуропр-ти) => ɗt/ɗτ=a▼2t.
Можно записать в цилиндрич координатах
(x=rcosφ,
y=rsinφ,
z=z):
ɗt/ɗτ=a(ɗ2t/ɗr2+1/r
*ɗt/ɗr+1/r2
*ɗ2t/ɗφ2+ɗ2t/ɗz2);
Для нестационарного двухмерного t
поля: ɗt/ɗτ=
a(ɗ2t/ɗx2+
ɗ2t/ɗy2);
Для нестац-го одномерного: ɗt/ɗτ=
a(ɗ2t/ɗx2).
Стац
поле-это
поле, в кот t’=f(x,y,z)=const.
Если t=const=>левая
часть всех ур-й=0, «а» отбрасываем и
записываем 3 ур-я. \\\ Ур-е с ▼ позволяет
решить задачу, когда нет источников
теплоты. Если есть, то к правой части
прибавляем W/cρ,
(W-интенсивность
источника).
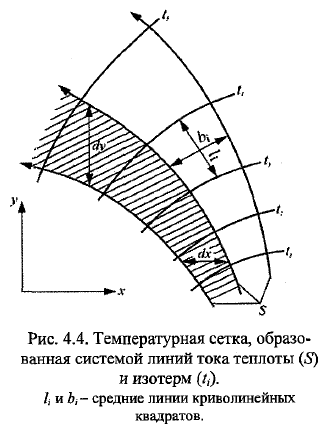
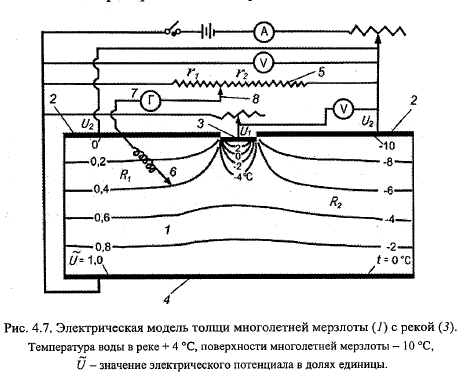 Б)
Графический метод ( закон рисунка).
Предусматривает построение ортогональной
сетки (ОС), состоящей из изотер и линий
тока теплоты. (Изотермы- линии с
одинаковыми значениями температур).
ОС –система криволинейных квадратов,
средние линии которых равны (li=bi).
Для решения задачи д.б. задан контур
плоского тела и граничные условия 1го
рода. Метод удобен для быстрого, но
приближённого получения рез-тов.
Построив сетку, определяем тепловой
поток в теле: Q=qстn=∑
λ дt/li
*bi.
qст-
тепловой поток струи, n-число
струй в ОС, bi-ширина
струи, li-длина
клетки.
Б)
Графический метод ( закон рисунка).
Предусматривает построение ортогональной
сетки (ОС), состоящей из изотер и линий
тока теплоты. (Изотермы- линии с
одинаковыми значениями температур).
ОС –система криволинейных квадратов,
средние линии которых равны (li=bi).
Для решения задачи д.б. задан контур
плоского тела и граничные условия 1го
рода. Метод удобен для быстрого, но
приближённого получения рез-тов.
Построив сетку, определяем тепловой
поток в теле: Q=qстn=∑
λ дt/li
*bi.
qст-
тепловой поток струи, n-число
струй в ОС, bi-ширина
струи, li-длина
клетки.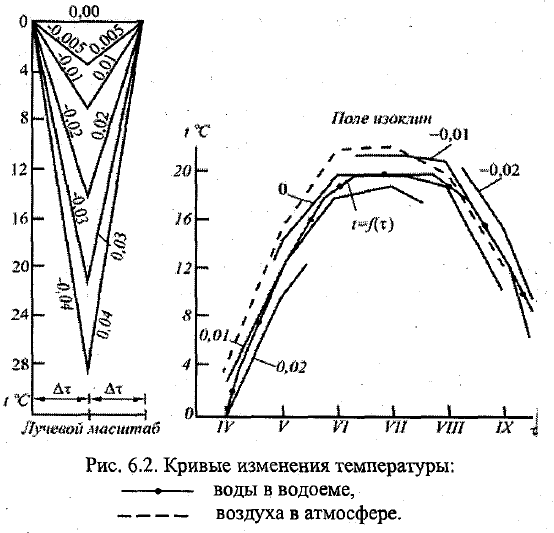 основе метода – ур-е теплового баланса
для нест-го t-го
поля: cρH
ɗt/ɗτ=∑Q.
=> Интегрирование уравнения dt/dτ
= - f(t)+φ(τ)
производят графически по методу
изоклин, предложенному еще Эйлером.
Рассмотрим этот метод на примере
расчета средних месячных значений t
воды для летнего периода года. Расчетный
интервал времени зависит от интервала
за который даются средние метео-
характеристики. Чем короче интервал
времени, тем точнее решается задача.
В начале для каждого летнего месяца
определяем f(t) в предположении, что
средняя месячная t
воды (в каждом месяце) будет меняться
в пределах (например, от 0 до 25 °С).
Полученные значения функции наносим
на график, в результате получим число
кривых, равных числу летних месяцев.
Затем вычисляем φ(τ) для каждого месяца
интересующего нас периода и строим
график. Затем перейдем к построению
поля изоклин. Потом значение dt/dτ
задаём равным 0,02; 0,01; 0,00; -0,01; -0,02 и тд.
и определяем по уравнению
функцию
f(t)
для каждого месяца, при этом значения
φ(τ) снимаем с соответствующего графика.
Затем по значениям функции f(t)
по графику определяем температуру
t. Полученные значения температуры
для всех заданных dt/dτ
наносим на рис. в координатах t, τ.
Соединяя ломаными линиями точки с
одинаковыми значениями dt/dτ, получим
поле изоклин. Изоклина
- это линия, для всех точек которой
производная имеет одно и то же значение.
На этом же рисунке строим лучевой
масштаб производных dt/dτ , который
является вспомогательным для нахождения
кривой t = f(
τ ) в поле изоклин. Масштабы координат
поля изоклин и лучевого принимаются
одинаковыми. Чтобы построить лучевой
масштаб, необходимо задать значения
градиента температуры. Предположим,
что дt/дτ
= 0,01. Тогда при интервале времени дτ:
= 1 мес. = 720 ч перепад температуры дt =
7,2 °С, то для градиента 0,02 будет
дt=14,4°С.
После в поле координат лучевого
масштаба строим линии, принятым
градиентам: 0,02; 0,01; и т.д., которые
выписываем у этих линий. Построение
интересующей нас интегральной
температурной кривой t = f
(τ) с помощью лучевого масштаба начинаем
с месяца, когда значение температуры
известно. Если температура воды равна
О °С 15/IV. Через точку с этой датой
проходит линия поля изоклин со значением
0,02. Из этого следует, что градиент
температуры в этой точке равен 0,02.
Поэтому через эту точку нужно провести
луч лучевого масштаба, отвечающий
значению 0,02, и продолжить его до
середины между изоклиной 0,02 и ближайшей
к ней 0,01, т. е. до изоклины 0,015. Здесь
луч изменит свое направление, так как
линия пойдет под углом, соответствующим
изоклине 0,015, и дойдет до изоклины
0,01, где наклон его снова изменится, и
т. д. Таким образом, полученная ломаная
линия будет кривой хода средней
температуры воды за безледоставный
период.
основе метода – ур-е теплового баланса
для нест-го t-го
поля: cρH
ɗt/ɗτ=∑Q.
=> Интегрирование уравнения dt/dτ
= - f(t)+φ(τ)
производят графически по методу
изоклин, предложенному еще Эйлером.
Рассмотрим этот метод на примере
расчета средних месячных значений t
воды для летнего периода года. Расчетный
интервал времени зависит от интервала
за который даются средние метео-
характеристики. Чем короче интервал
времени, тем точнее решается задача.
В начале для каждого летнего месяца
определяем f(t) в предположении, что
средняя месячная t
воды (в каждом месяце) будет меняться
в пределах (например, от 0 до 25 °С).
Полученные значения функции наносим
на график, в результате получим число
кривых, равных числу летних месяцев.
Затем вычисляем φ(τ) для каждого месяца
интересующего нас периода и строим
график. Затем перейдем к построению
поля изоклин. Потом значение dt/dτ
задаём равным 0,02; 0,01; 0,00; -0,01; -0,02 и тд.
и определяем по уравнению
функцию
f(t)
для каждого месяца, при этом значения
φ(τ) снимаем с соответствующего графика.
Затем по значениям функции f(t)
по графику определяем температуру
t. Полученные значения температуры
для всех заданных dt/dτ
наносим на рис. в координатах t, τ.
Соединяя ломаными линиями точки с
одинаковыми значениями dt/dτ, получим
поле изоклин. Изоклина
- это линия, для всех точек которой
производная имеет одно и то же значение.
На этом же рисунке строим лучевой
масштаб производных dt/dτ , который
является вспомогательным для нахождения
кривой t = f(
τ ) в поле изоклин. Масштабы координат
поля изоклин и лучевого принимаются
одинаковыми. Чтобы построить лучевой
масштаб, необходимо задать значения
градиента температуры. Предположим,
что дt/дτ
= 0,01. Тогда при интервале времени дτ:
= 1 мес. = 720 ч перепад температуры дt =
7,2 °С, то для градиента 0,02 будет
дt=14,4°С.
После в поле координат лучевого
масштаба строим линии, принятым
градиентам: 0,02; 0,01; и т.д., которые
выписываем у этих линий. Построение
интересующей нас интегральной
температурной кривой t = f
(τ) с помощью лучевого масштаба начинаем
с месяца, когда значение температуры
известно. Если температура воды равна
О °С 15/IV. Через точку с этой датой
проходит линия поля изоклин со значением
0,02. Из этого следует, что градиент
температуры в этой точке равен 0,02.
Поэтому через эту точку нужно провести
луч лучевого масштаба, отвечающий
значению 0,02, и продолжить его до
середины между изоклиной 0,02 и ближайшей
к ней 0,01, т. е. до изоклины 0,015. Здесь
луч изменит свое направление, так как
линия пойдет под углом, соответствующим
изоклине 0,015, и дойдет до изоклины
0,01, где наклон его снова изменится, и
т. д. Таким образом, полученная ломаная
линия будет кривой хода средней
температуры воды за безледоставный
период.
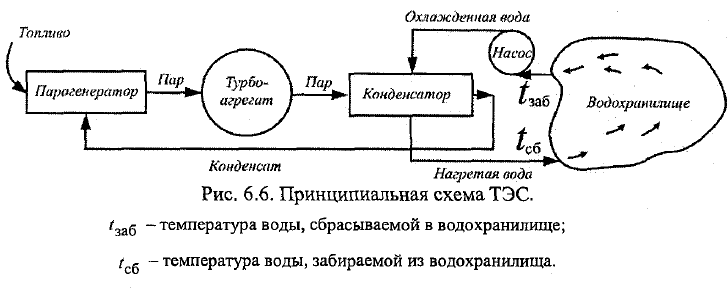
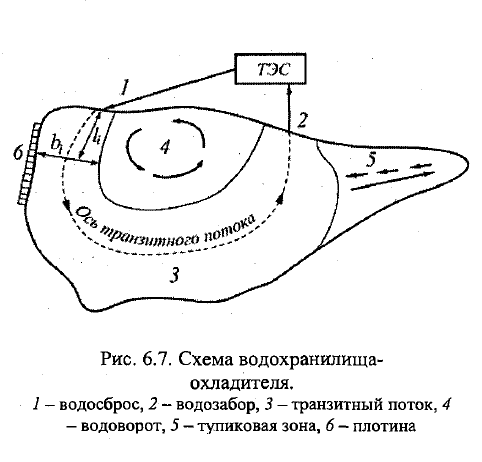
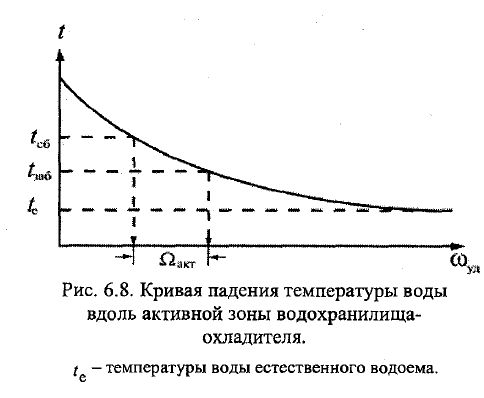
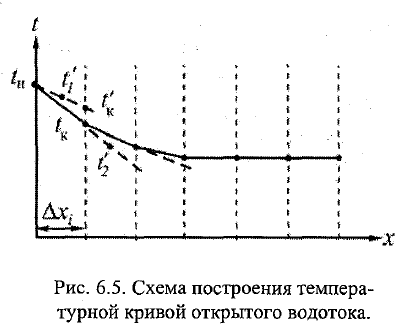 сп-ся
диф.ур-е, описывающее температурное
поле потока. По разным причинам
уравнение ɗt/ɗτ+vx
ɗt/ɗx+
vy
ɗt/ɗy
+vz
ɗt/ɗz
= λт/(cρ)
(ɗ2t/ɗx2
+ ɗ2t/ɗy2
+ɗ2t/ɗz2
), (v-проекция
скорости) решить не удается, поэтому
его упрощают. При рассмотрении
температурного режима потока с более
или менее прямолинейным течением
принимают, что Vx=Vy=0.
Пренебрегают
2ми производными от t
по длине и ширине потока из-за их
малости. Ур-е приобретает вид:
ɗt/ɗτ+vx*ɗt/ɗx=(λт
/cp)*(
ɗ2t/ɗz2).
Для установ-ся t-го
режима ( dt/dτ
= 0),
проинтегрируем vx*ɗt/ɗx=(λт
/cp)*(
ɗ2t/ɗz2)
и запишем в конечных разностях дt/дx=(
∑Q)/(cρvxH),
где дt=(tк
–tн)
отрезка дx;
дx=vx*дτ.
Можно заменить vxН
= qв
; где qв
-уд.расход
воды. Отдельные слагаемые суммы
теплопотоков зависят от искомой t
воды на участке, т.е. от tср=(tн+tк)/2.
Это обусловливает выбор метода
последовательных приближений, т.е.
задается ориентировочно искомое
значение температуры tк.,
затем
определяются теплопотоки через
поверхности водотока, после чего
решается уравнение в конечных разностях.
Решением этого уравнения считается
значение t,
которое совпадет с заданным ее
значением. Если не совпадает – расчёты
повторяют, задач новое значение tк.
\\\ Проектирование t-й
кривой реки по её длине вып-ся по ур-ю
ɗt/ɗx=(
∑Q)/(cρvxH)
по схеме. Водоток по длине разбивается
на участки протяжённостью дxi,
в зав-ти от времени добегания дτ.
В поле координат t,x
на 1м участке проводят отрезок t-й
кривой tнt’к.
Начало кривой опр-ся tн,
конец-t’к.
Средняя t
, т.е. t’1,
позволяет опр-ть тепловые потоки через
водную пов-ть (граничн усл), кот
подставляются в ур-е в конечн.разностях.
Далее следующ участок. Экстраполируют
дx,
снимают t’2
и т.д.
сп-ся
диф.ур-е, описывающее температурное
поле потока. По разным причинам
уравнение ɗt/ɗτ+vx
ɗt/ɗx+
vy
ɗt/ɗy
+vz
ɗt/ɗz
= λт/(cρ)
(ɗ2t/ɗx2
+ ɗ2t/ɗy2
+ɗ2t/ɗz2
), (v-проекция
скорости) решить не удается, поэтому
его упрощают. При рассмотрении
температурного режима потока с более
или менее прямолинейным течением
принимают, что Vx=Vy=0.
Пренебрегают
2ми производными от t
по длине и ширине потока из-за их
малости. Ур-е приобретает вид:
ɗt/ɗτ+vx*ɗt/ɗx=(λт
/cp)*(
ɗ2t/ɗz2).
Для установ-ся t-го
режима ( dt/dτ
= 0),
проинтегрируем vx*ɗt/ɗx=(λт
/cp)*(
ɗ2t/ɗz2)
и запишем в конечных разностях дt/дx=(
∑Q)/(cρvxH),
где дt=(tк
–tн)
отрезка дx;
дx=vx*дτ.
Можно заменить vxН
= qв
; где qв
-уд.расход
воды. Отдельные слагаемые суммы
теплопотоков зависят от искомой t
воды на участке, т.е. от tср=(tн+tк)/2.
Это обусловливает выбор метода
последовательных приближений, т.е.
задается ориентировочно искомое
значение температуры tк.,
затем
определяются теплопотоки через
поверхности водотока, после чего
решается уравнение в конечных разностях.
Решением этого уравнения считается
значение t,
которое совпадет с заданным ее
значением. Если не совпадает – расчёты
повторяют, задач новое значение tк.
\\\ Проектирование t-й
кривой реки по её длине вып-ся по ур-ю
ɗt/ɗx=(
∑Q)/(cρvxH)
по схеме. Водоток по длине разбивается
на участки протяжённостью дxi,
в зав-ти от времени добегания дτ.
В поле координат t,x
на 1м участке проводят отрезок t-й
кривой tнt’к.
Начало кривой опр-ся tн,
конец-t’к.
Средняя t
, т.е. t’1,
позволяет опр-ть тепловые потоки через
водную пов-ть (граничн усл), кот
подставляются в ур-е в конечн.разностях.
Далее следующ участок. Экстраполируют
дx,
снимают t’2
и т.д.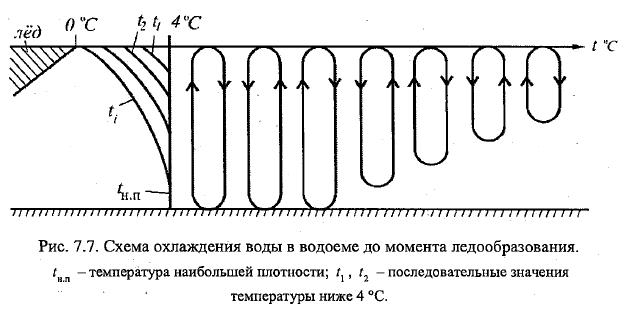
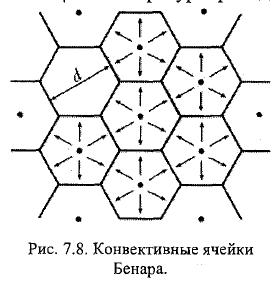
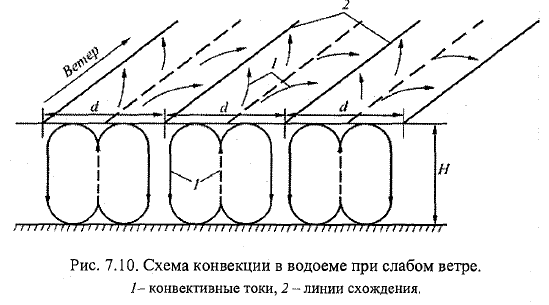
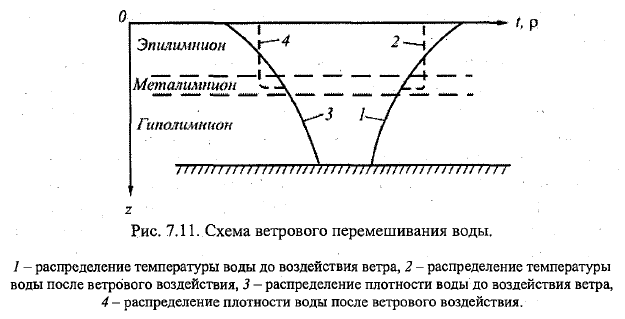
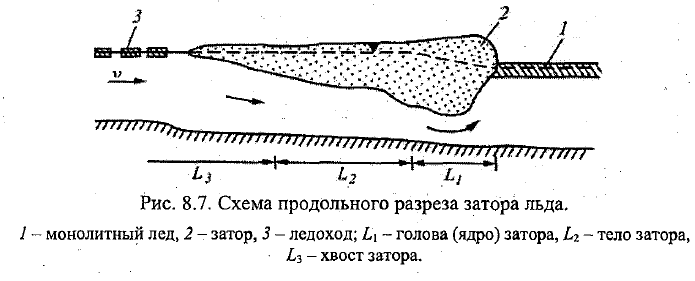
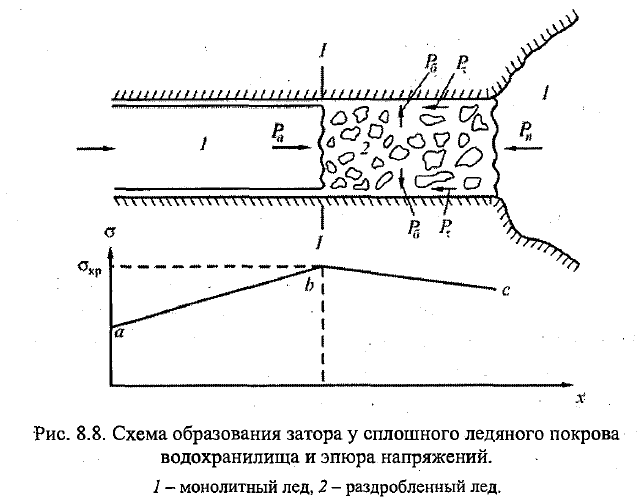
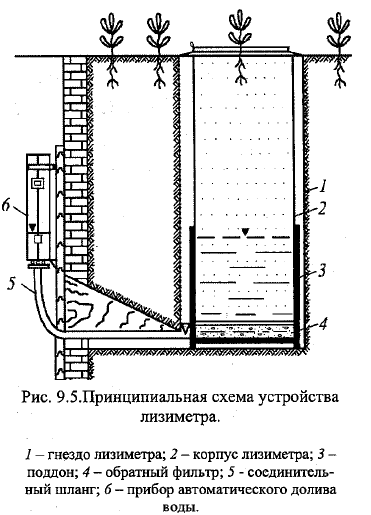 9.
Экспериментальные методы определения
испарения с почвы. Измерение
суммарного испарения с пов-ти почвы,
покрытой растительностью, и испарения
с пов-ти затенённой почвы осущ-ся с
помощью почвенный испарителей
–ГГИ-500-50, ГГИ-500-100, гидравлического
почвенного испарителя малой модели
и лизиметра ГР-80. В основе определения
ур-е водного баланса, применительно
к монолиту испарителя: Е=Х+(B1-B2)-y,
где количество воды за период наблюдений
дτ: Е-испарившейся, Х-выпавших осадков,
у- просочившейся через монолит. В1,В1-
массы монолита в нач и конце дτ. Для
определения массы монолита, он
взвешивается на мех-х весах или
гидравлич способом. Испарители ГГИ-500
применяются для изучения испарения
с пов-ти верхнего деятельного слоя
почвогрунтов (ПГ). После взвешивания
испаритель опускается в спец
изготовленное из металла цилиндрическое
гнездо, вкопанное в ПГ. Просочившаяся
через монолит вода собирается спец
сосудом, прикреплённым снизу. Кол-во
осадков опр с помощью дождемера, кот
установлен рядом с испарителем.
«+»-простота измерения и получение
сведений за любой интервал времени,
«-»-невысокая точность (т.к. почва
отделена от грунтовых вод, металлическая
стенка искажает теплообмен, корневая
система травмируется при зарядке
монолитом).\\\ Гидравлич почвенный
испаритель (ГПИ) даёт возможность
измерять полусуточные и ежечасные
значения испарения путём гидростатич
взвешивания (фиксирование вертикального
перемещения ГПИ с монолитом, плавающего
в воде отн-но уровня воды в бассейне.
В зав-ти от испарения уровень воды
меняется, т.е. в зав-ти от изменения
веса). \\\ Лизиметр применяется для
измерения суммарного испарения,
расхода грунтовых вод, при глубине их
залегания не более 5 м. Измерение
запасов почвенной влаги в монолите
опр-ся с помощью почвенных влагометров
или путём его взвешивания на весах.
Зарядка цилиндра почвенным монолитом
произв вдавливанием его в почву с
последующ окапыванием почвы вокруг.
9.
Экспериментальные методы определения
испарения с почвы. Измерение
суммарного испарения с пов-ти почвы,
покрытой растительностью, и испарения
с пов-ти затенённой почвы осущ-ся с
помощью почвенный испарителей
–ГГИ-500-50, ГГИ-500-100, гидравлического
почвенного испарителя малой модели
и лизиметра ГР-80. В основе определения
ур-е водного баланса, применительно
к монолиту испарителя: Е=Х+(B1-B2)-y,
где количество воды за период наблюдений
дτ: Е-испарившейся, Х-выпавших осадков,
у- просочившейся через монолит. В1,В1-
массы монолита в нач и конце дτ. Для
определения массы монолита, он
взвешивается на мех-х весах или
гидравлич способом. Испарители ГГИ-500
применяются для изучения испарения
с пов-ти верхнего деятельного слоя
почвогрунтов (ПГ). После взвешивания
испаритель опускается в спец
изготовленное из металла цилиндрическое
гнездо, вкопанное в ПГ. Просочившаяся
через монолит вода собирается спец
сосудом, прикреплённым снизу. Кол-во
осадков опр с помощью дождемера, кот
установлен рядом с испарителем.
«+»-простота измерения и получение
сведений за любой интервал времени,
«-»-невысокая точность (т.к. почва
отделена от грунтовых вод, металлическая
стенка искажает теплообмен, корневая
система травмируется при зарядке
монолитом).\\\ Гидравлич почвенный
испаритель (ГПИ) даёт возможность
измерять полусуточные и ежечасные
значения испарения путём гидростатич
взвешивания (фиксирование вертикального
перемещения ГПИ с монолитом, плавающего
в воде отн-но уровня воды в бассейне.
В зав-ти от испарения уровень воды
меняется, т.е. в зав-ти от изменения
веса). \\\ Лизиметр применяется для
измерения суммарного испарения,
расхода грунтовых вод, при глубине их
залегания не более 5 м. Измерение
запасов почвенной влаги в монолите
опр-ся с помощью почвенных влагометров
или путём его взвешивания на весах.
Зарядка цилиндра почвенным монолитом
произв вдавливанием его в почву с
последующ окапыванием почвы вокруг.
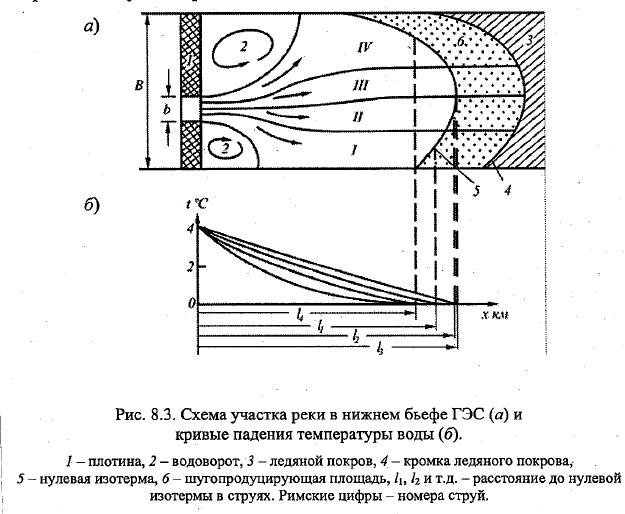 6.
Расчёт полыньи и количества шуги,
образующейся в ней. Покажите необходимость
учёта длины полыньи на примере
Красноярской ГЭС и способы её уменьшения.
Полынья –н езамерзшее
или уже растаявшее
место на ледяной поверхности реки,
водоема.
После установления ледостава на реке
в нижнем бьефе ГЭС в течение всего
зимнего периода наблюдается полынья,
длина которой может достигать 100км и
более. Размер полыньи зависит от t
сбрасываемой воды, теплоотдачи воды
в атм-ру, от скоростного режима реки
на этом участке. Открытые водные пов-ти
реки зимой явл-ся производителями
шуги и тумана. Шуга при остановке может
образовать зажор=> поднятие уровня
воды и затопление тер-рий. Из-за тумана
может произойти обледенение окр
тер-рий. Расчёт
площади: 1). Гидравлическая часть
Построение плана течений в нижнем
бьефе ГЭС по закону расширения струи
Бернадского b=b0(h0/h)exp(g(n2/hср4/3
–Ix/vср2)l),
b0,h0,b,h-ширина
и глубина транзитного (циркуляционного)
потока (ТП) в нач и кон сечениях участка
длиной l.
n-коэф
шероховатости, Ix-продольный
уклон. Намечают ожидаему ось ТП (от
водосброса к водозабору). Рассчитывают
b1,
на расстоянии
l1.
Повторяются расчёты для каждого
очередного участка потока длиной
li.Через
концы полученных отрезков ширины bi
проводят огибающие линии, кот явл
границами ТП. Построенный план течений
должен содержать 4-5 струй. 2.теплотехническая
Исп ур-е теплового баланса для водотока
dt/dx=(bc∑Q)/(cρQc),
bc,Qc-ширина
и расход струи, ∑Q-потери
теплоты на зеркале водоёма, t-темп.
По построенным графикам можно будет
определить для каждой струи расстояние
от нач створа до точки с t=0С,
т.е. длину полыньи. Линия, соединяющая
найденный точки с нулевой t
воды для каждой струи- нулевая изотерма
(НИ). Если расчёт НИ выполнен для
утнановивщ метео условий, то НИ будет
совпадать с кромкой сплошного лед
покрова. Если пройдёт волна холода,
то НИ продвинется вверх по реке, если
тепло-вниз по реке (лёд будет таять).
Шугообразующая (Ш) площадь полыньи –
не вся площадь открытой водной пов-ти,
а только часть между НИ и кромкой
сплошного лед покрова, т.е. где
наблюдается переохлаждение воды.
\\\\\ Qш=(1-exp(-qτ/(Lкр
a)))
v
a
B,
Qш-расход
шуги,q-плотность
теплового потока через водную пов-ть,
t-время
добегания ледяных образований от НИ
до кромки ЛП, а-кол-во льда на ед пов-ти,
v-ср
скорость шугохода, В-ширина реки.
Красноярская.
(Енисей, Карское море). После постройки
ГЭС появилась незамерзающая полынья.
Предполагалось, что полынья будет 20
км, оказалось 200 км. Климат стал более
влажным из-за большего кол-ва незамерзающ
воды зимой=> обмерзают провода,
троллейбусы не ходят). Енисей в районе
Красноярска перестал замерзать.
повысился уровень заболевания населения
(бонхит, орви). Чтобы её уменьшить
пытались, например, охлаждать
искусственным снегом, но нужно слишком
много снега; установить аэродинамические
трубы, чтобы охлаждать воздух; пустить
рядом приток через трубы чтобы охладить
воду. Для решения можно построить
контррегулятор, который обеспечит
выравнивание расходов и уровней воды
ниже створа контррегулятора, что
позволит значительно уменьшить длину
полыньи и создаст условия для образования
ледяного покрова в нижнем бьефе и его
сохранения на весь зимний период. в
верхнем бьефе, подо льдом, вода холоднее.
нужно утсновить трубу, соединующую
верхний и нижний бьеф. по ней будет
стекать холодная водя в нижний бьеф
(t от 0 и ниже)=>там происходит замерзание
6.
Расчёт полыньи и количества шуги,
образующейся в ней. Покажите необходимость
учёта длины полыньи на примере
Красноярской ГЭС и способы её уменьшения.
Полынья –н езамерзшее
или уже растаявшее
место на ледяной поверхности реки,
водоема.
После установления ледостава на реке
в нижнем бьефе ГЭС в течение всего
зимнего периода наблюдается полынья,
длина которой может достигать 100км и
более. Размер полыньи зависит от t
сбрасываемой воды, теплоотдачи воды
в атм-ру, от скоростного режима реки
на этом участке. Открытые водные пов-ти
реки зимой явл-ся производителями
шуги и тумана. Шуга при остановке может
образовать зажор=> поднятие уровня
воды и затопление тер-рий. Из-за тумана
может произойти обледенение окр
тер-рий. Расчёт
площади: 1). Гидравлическая часть
Построение плана течений в нижнем
бьефе ГЭС по закону расширения струи
Бернадского b=b0(h0/h)exp(g(n2/hср4/3
–Ix/vср2)l),
b0,h0,b,h-ширина
и глубина транзитного (циркуляционного)
потока (ТП) в нач и кон сечениях участка
длиной l.
n-коэф
шероховатости, Ix-продольный
уклон. Намечают ожидаему ось ТП (от
водосброса к водозабору). Рассчитывают
b1,
на расстоянии
l1.
Повторяются расчёты для каждого
очередного участка потока длиной
li.Через
концы полученных отрезков ширины bi
проводят огибающие линии, кот явл
границами ТП. Построенный план течений
должен содержать 4-5 струй. 2.теплотехническая
Исп ур-е теплового баланса для водотока
dt/dx=(bc∑Q)/(cρQc),
bc,Qc-ширина
и расход струи, ∑Q-потери
теплоты на зеркале водоёма, t-темп.
По построенным графикам можно будет
определить для каждой струи расстояние
от нач створа до точки с t=0С,
т.е. длину полыньи. Линия, соединяющая
найденный точки с нулевой t
воды для каждой струи- нулевая изотерма
(НИ). Если расчёт НИ выполнен для
утнановивщ метео условий, то НИ будет
совпадать с кромкой сплошного лед
покрова. Если пройдёт волна холода,
то НИ продвинется вверх по реке, если
тепло-вниз по реке (лёд будет таять).
Шугообразующая (Ш) площадь полыньи –
не вся площадь открытой водной пов-ти,
а только часть между НИ и кромкой
сплошного лед покрова, т.е. где
наблюдается переохлаждение воды.
\\\\\ Qш=(1-exp(-qτ/(Lкр
a)))
v
a
B,
Qш-расход
шуги,q-плотность
теплового потока через водную пов-ть,
t-время
добегания ледяных образований от НИ
до кромки ЛП, а-кол-во льда на ед пов-ти,
v-ср
скорость шугохода, В-ширина реки.
Красноярская.
(Енисей, Карское море). После постройки
ГЭС появилась незамерзающая полынья.
Предполагалось, что полынья будет 20
км, оказалось 200 км. Климат стал более
влажным из-за большего кол-ва незамерзающ
воды зимой=> обмерзают провода,
троллейбусы не ходят). Енисей в районе
Красноярска перестал замерзать.
повысился уровень заболевания населения
(бонхит, орви). Чтобы её уменьшить
пытались, например, охлаждать
искусственным снегом, но нужно слишком
много снега; установить аэродинамические
трубы, чтобы охлаждать воздух; пустить
рядом приток через трубы чтобы охладить
воду. Для решения можно построить
контррегулятор, который обеспечит
выравнивание расходов и уровней воды
ниже створа контррегулятора, что
позволит значительно уменьшить длину
полыньи и создаст условия для образования
ледяного покрова в нижнем бьефе и его
сохранения на весь зимний период. в
верхнем бьефе, подо льдом, вода холоднее.
нужно утсновить трубу, соединующую
верхний и нижний бьеф. по ней будет
стекать холодная водя в нижний бьеф
(t от 0 и ниже)=>там происходит замерзание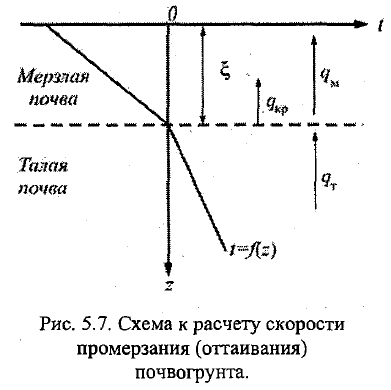 7.
Задача Стефана для промерзающих
(оттаивающих) грунтов.
Когда t
поле опр-ся для среды, меняющей агрегатн
сост с поглощением или выделением
тепловой энергии (влажные
замерзающие/оттаивающие почвы), нужно
учитывать условие на границе талой и
мёрзлой среды. –усл С. Оно заключается
в том , что разность интенсивностей
тепловых потоков, поступающего от
талой среды к границе мерзлой и
уходящего от этой границы через мерзлый
слой, идет на таяние льда в мерзлом
слое. При замерзании почвы тепловой
поток из талого слоя суммируется с
теплотой кристаллизации воды и
отводится через мерзлый слой в
атмосферу. ξ-толщина мерзлого слоя,
t-
ось абсцисс, z-ось
ординат, qм-
интенсивность теплового потока в
мерзлом на границе с талым (qт);
qкр-
интенсивность потока теплоты
кристаллизации => согласно закону
сохранения тепл.энергии qм=
qт+
qкр.
Выразим
интенсивность через Фурье: qт=
-λт
ɗt/ɗz|+0;
qм=
-λм
ɗt/ɗz|-0
(+/- 0 показывают, что поток рассматривается
со стороны талого/мёрзлого слоя почвы).
Пусть W
-объем воды в ед объема почвы. qкр=
-(ɗξ/ɗт) Wρ
Lкр.
Решая совместно, найдем выражение
для скорости промерзании почвы ( и
оттаивания, только справа у уменьшаемого
и вычитаемого необходимо поменять
знаки)
7.
Задача Стефана для промерзающих
(оттаивающих) грунтов.
Когда t
поле опр-ся для среды, меняющей агрегатн
сост с поглощением или выделением
тепловой энергии (влажные
замерзающие/оттаивающие почвы), нужно
учитывать условие на границе талой и
мёрзлой среды. –усл С. Оно заключается
в том , что разность интенсивностей
тепловых потоков, поступающего от
талой среды к границе мерзлой и
уходящего от этой границы через мерзлый
слой, идет на таяние льда в мерзлом
слое. При замерзании почвы тепловой
поток из талого слоя суммируется с
теплотой кристаллизации воды и
отводится через мерзлый слой в
атмосферу. ξ-толщина мерзлого слоя,
t-
ось абсцисс, z-ось
ординат, qм-
интенсивность теплового потока в
мерзлом на границе с талым (qт);
qкр-
интенсивность потока теплоты
кристаллизации => согласно закону
сохранения тепл.энергии qм=
qт+
qкр.
Выразим
интенсивность через Фурье: qт=
-λт
ɗt/ɗz|+0;
qм=
-λм
ɗt/ɗz|-0
(+/- 0 показывают, что поток рассматривается
со стороны талого/мёрзлого слоя почвы).
Пусть W
-объем воды в ед объема почвы. qкр=
-(ɗξ/ɗт) Wρ
Lкр.
Решая совместно, найдем выражение
для скорости промерзании почвы ( и
оттаивания, только справа у уменьшаемого
и вычитаемого необходимо поменять
знаки)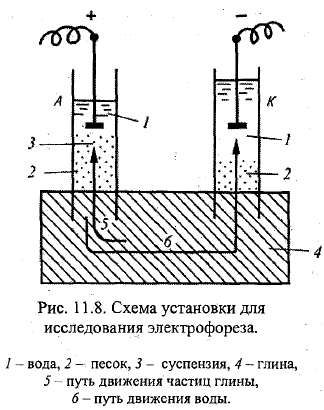
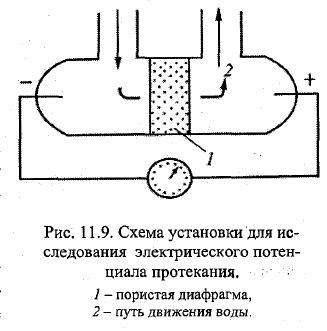
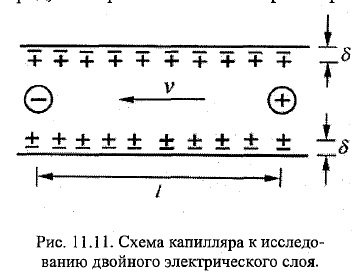
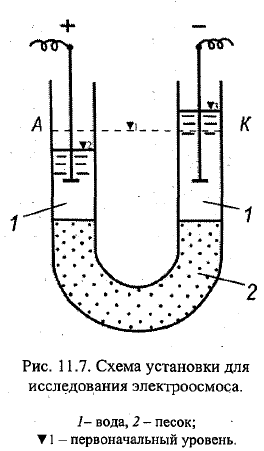
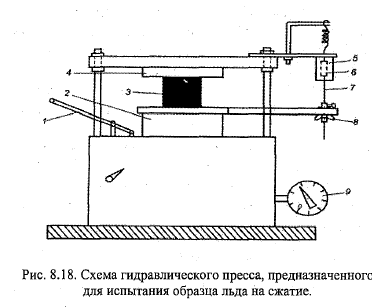
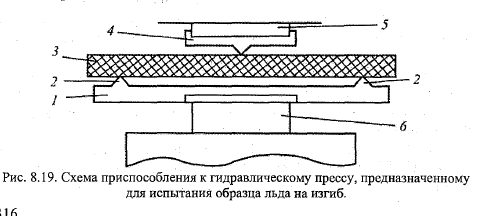
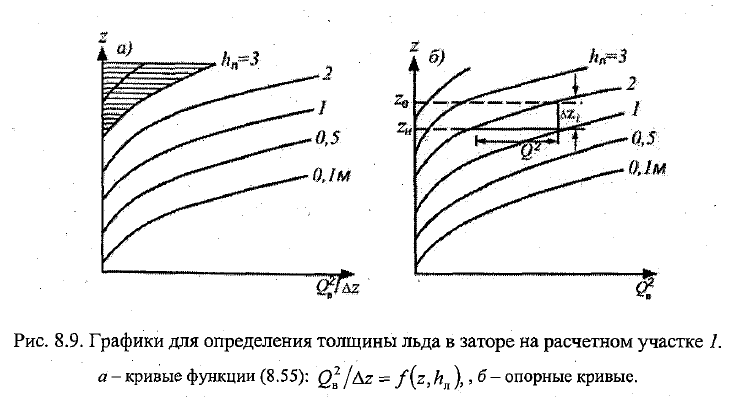 1.
Заторообразование и расчёт количества
льда в заторе.
Затор
– скопление льдин в русле реки во
время ледохода, вызывающее уменьшение
водного сечения реки и подъём уровня
воды (конец зимы и весна). Прямое
измерение основных параметров затора
очень сложно, методы дистанционного
не разработаны. =>Косвенный метод
исп-ют. Основан на применении опорных
кривых Бернадского и позволяет по
сведениям об уровнях воды в разных
створах и расходе воды опр-ть толщину
льда по длине затора=>его кол-во в
заторе. Расход
воды Qв=vF,
F-площадь
поп-го сечения., v=Cкорень(RI),
C=1/n
R1/6
=>Qв2/дz=R4/3
F2/(n2L)-для
открытого потока; Qв2/дz=R4/3
(F2-Bhл)2/(nпр2L)-для
закрытого потока (при ЛП, заторе).
В-ширина реки, nпр-приведённый
коэф шероховатости. дz-перепад
уровней на расстоянии L.
График (z.
Qв2).
Кривые строятся п предположении, что
будет наблюдаться толщина льда в
заторе, например :0.1,0..5,1,2,3 м и т.д. Чтобы
построить опорные кривые
для расчётных участков, по кот будем
опр-ть толщину льда в заторе, нужно
проинтегрировать левую часть посл-го
ур-я. Значения интеграла –посл-е
площади между осью z
и соотв кривой hi.
При помощт опорных кривых (ОК) можно
опр толщину льда. Нужно вычислить
перепад уровней дzi=zв-zн,
найти Qв2
и по этим данным построить прямоугольные
треугольники на прозрачной бумаге.
Затем,
прикладывая поочерёдно каждый из тр-в
к графикам ОК, перемещаем их вдоль
гор-й оси, придерживаясь отметок zв,zн
. Решением
задачи будет совпадение концов
гипотенузы тр-ка с одной из ОК, соотв
опр-му значению hл.
После опр-я толщины на каждом расчётном
участке затора опр кол-во льда в нём:
mзат=ρл∑(Bihлli),
Bihлli
-средние
на раст-м участве ширина, толщина льда
и длина участка, n-число
расч-х участков, ρл
-плотность
льда в заторе.
1.
Заторообразование и расчёт количества
льда в заторе.
Затор
– скопление льдин в русле реки во
время ледохода, вызывающее уменьшение
водного сечения реки и подъём уровня
воды (конец зимы и весна). Прямое
измерение основных параметров затора
очень сложно, методы дистанционного
не разработаны. =>Косвенный метод
исп-ют. Основан на применении опорных
кривых Бернадского и позволяет по
сведениям об уровнях воды в разных
створах и расходе воды опр-ть толщину
льда по длине затора=>его кол-во в
заторе. Расход
воды Qв=vF,
F-площадь
поп-го сечения., v=Cкорень(RI),
C=1/n
R1/6
=>Qв2/дz=R4/3
F2/(n2L)-для
открытого потока; Qв2/дz=R4/3
(F2-Bhл)2/(nпр2L)-для
закрытого потока (при ЛП, заторе).
В-ширина реки, nпр-приведённый
коэф шероховатости. дz-перепад
уровней на расстоянии L.
График (z.
Qв2).
Кривые строятся п предположении, что
будет наблюдаться толщина льда в
заторе, например :0.1,0..5,1,2,3 м и т.д. Чтобы
построить опорные кривые
для расчётных участков, по кот будем
опр-ть толщину льда в заторе, нужно
проинтегрировать левую часть посл-го
ур-я. Значения интеграла –посл-е
площади между осью z
и соотв кривой hi.
При помощт опорных кривых (ОК) можно
опр толщину льда. Нужно вычислить
перепад уровней дzi=zв-zн,
найти Qв2
и по этим данным построить прямоугольные
треугольники на прозрачной бумаге.
Затем,
прикладывая поочерёдно каждый из тр-в
к графикам ОК, перемещаем их вдоль
гор-й оси, придерживаясь отметок zв,zн
. Решением
задачи будет совпадение концов
гипотенузы тр-ка с одной из ОК, соотв
опр-му значению hл.
После опр-я толщины на каждом расчётном
участке затора опр кол-во льда в нём:
mзат=ρл∑(Bihлli),
Bihлli
-средние
на раст-м участве ширина, толщина льда
и длина участка, n-число
расч-х участков, ρл
-плотность
льда в заторе.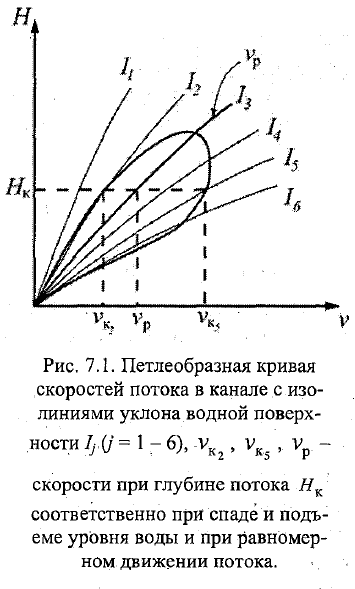 2.
Виды движения вод суши и уравнения их
описывающие.
Воды суши приходят в движение под
влиянием различных действующ на них
сил. 1. Для открытых потоков одна из
них-сила тяжести (гравитационное
течение).
Сила инерции-для отрытого потока- та
часть силы тяжести, на которую она
превышает силу трения потока о стенки
и о дно русла канала/реки. 2. Движение
под воздействием ветра. Имеет случайный
характер. Ветровое
течение (дрейфовое).
Сопровождается денивеляцией (уменьшение
уровня воды
из-за колебаний Ра). 3. Конвективное
течение.
(свободная конвекция). Обусловлено
разностью плотностей частиц воды,
вызванной термичсеким расслоением
водной среды. Также при разной солёности
или насыщенности взвешенными наносами.
\\\ Гравитационное.
Ламинарный
режим-направление
течения частиц жидкости опр-ся стенками
канала. Движение упорядоченное,
струйками, без перемешивания.
Турбулентный-движение
носит беспорядочный характер, сильное
перемешивание. Кроме поступат-го
движения есть сложные доп движения в
поперечном направлении. Стенки не
управляют течением, а обеспечивают
только главное направление. Скорости
изменяются по величине и направлению.
vp=Cкорень(RIp).
Для равном-го движ в безнапорном
потоке, модуль скорости W=Cкорень(R)=vp/I1/2.
R=ω/χ.
Коэф гидравлич сопротив-я λ=2gR/W2
, коэф
шероховатости n=R2/3/W;
\\\\ График (H/v).
–Линии уклона водной пов-ти. При
нестуновивш движении, т.е. при
петлеобразной кривой скоростей и
расходов, получаем 3 значения коэф для
конкретного наполнения русла.
Среднее-равномерн движ, крайние-кривые
подъёма и спала уровня воды (ошибочные,
т.к. нельзя применять Шези). v=vp±vv
. vv-средняя
скорость течения при отсутствии силы
трения, vp=ɑ1ipдI.=>Для
неустановивш-ся движ-я v=Cкорень(Hip)+ɑipдI.\\\
дI=I-ip
\\\Ур-е Сен-Венана I=1/g
ɗV/ɗt+V/g
ɗV/ɗx+Vp2/(C2H).
Левая часть уч-т силу тяжести, первые
два слагаемых справа – силу инерции,
последнее – силу трения.
2.
Виды движения вод суши и уравнения их
описывающие.
Воды суши приходят в движение под
влиянием различных действующ на них
сил. 1. Для открытых потоков одна из
них-сила тяжести (гравитационное
течение).
Сила инерции-для отрытого потока- та
часть силы тяжести, на которую она
превышает силу трения потока о стенки
и о дно русла канала/реки. 2. Движение
под воздействием ветра. Имеет случайный
характер. Ветровое
течение (дрейфовое).
Сопровождается денивеляцией (уменьшение
уровня воды
из-за колебаний Ра). 3. Конвективное
течение.
(свободная конвекция). Обусловлено
разностью плотностей частиц воды,
вызванной термичсеким расслоением
водной среды. Также при разной солёности
или насыщенности взвешенными наносами.
\\\ Гравитационное.
Ламинарный
режим-направление
течения частиц жидкости опр-ся стенками
канала. Движение упорядоченное,
струйками, без перемешивания.
Турбулентный-движение
носит беспорядочный характер, сильное
перемешивание. Кроме поступат-го
движения есть сложные доп движения в
поперечном направлении. Стенки не
управляют течением, а обеспечивают
только главное направление. Скорости
изменяются по величине и направлению.
vp=Cкорень(RIp).
Для равном-го движ в безнапорном
потоке, модуль скорости W=Cкорень(R)=vp/I1/2.
R=ω/χ.
Коэф гидравлич сопротив-я λ=2gR/W2
, коэф
шероховатости n=R2/3/W;
\\\\ График (H/v).
–Линии уклона водной пов-ти. При
нестуновивш движении, т.е. при
петлеобразной кривой скоростей и
расходов, получаем 3 значения коэф для
конкретного наполнения русла.
Среднее-равномерн движ, крайние-кривые
подъёма и спала уровня воды (ошибочные,
т.к. нельзя применять Шези). v=vp±vv
. vv-средняя
скорость течения при отсутствии силы
трения, vp=ɑ1ipдI.=>Для
неустановивш-ся движ-я v=Cкорень(Hip)+ɑipдI.\\\
дI=I-ip
\\\Ур-е Сен-Венана I=1/g
ɗV/ɗt+V/g
ɗV/ɗx+Vp2/(C2H).
Левая часть уч-т силу тяжести, первые
два слагаемых справа – силу инерции,
последнее – силу трения.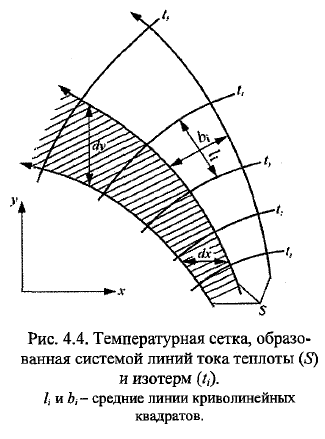 етод
конечных разностей (графический)
состоит в
том, что в дифференциальном уравнении
теплопроводности, которое следует
решить, все бесконечно малые разности
(дифференциалы) заменяются конечными,
но малыми разностными величинами.
Достоинством метода является возможность
решить весьма сложные задачи. К
недостаткам метода относятся: отсутствие
общего решения задач; необходимость
производства вычислений для всего
тела и для всего периода, предшествующего
моменту времени, для которого
производится вычисление температуры,
трудоемкость метода. Предусматривает
построение ортогональной сетки (ОС),
состоящей из изотер и линий тока
теплоты. (Изотермы- линии с одинаковыми
значениями температур). ОС –система
криволинейных квадратов, средние
линии которых равны (li=bi).
Для решения задачи д.б. задан контур
плоского тела и граничные условия 1го
рода. Метод удобен для быстрого, но
приближённого получения рез-тов.
Построив сетку, определяем тепловой
поток в теле: Q=qстn=∑
λ дt/li
*bi.
qст-
тепловой поток струи, n-число
струй в ОС, bi-ширина
струи, li-длина
клетки.
етод
конечных разностей (графический)
состоит в
том, что в дифференциальном уравнении
теплопроводности, которое следует
решить, все бесконечно малые разности
(дифференциалы) заменяются конечными,
но малыми разностными величинами.
Достоинством метода является возможность
решить весьма сложные задачи. К
недостаткам метода относятся: отсутствие
общего решения задач; необходимость
производства вычислений для всего
тела и для всего периода, предшествующего
моменту времени, для которого
производится вычисление температуры,
трудоемкость метода. Предусматривает
построение ортогональной сетки (ОС),
состоящей из изотер и линий тока
теплоты. (Изотермы- линии с одинаковыми
значениями температур). ОС –система
криволинейных квадратов, средние
линии которых равны (li=bi).
Для решения задачи д.б. задан контур
плоского тела и граничные условия 1го
рода. Метод удобен для быстрого, но
приближённого получения рез-тов.
Построив сетку, определяем тепловой
поток в теле: Q=qстn=∑
λ дt/li
*bi.
qст-
тепловой поток струи, n-число
струй в ОС, bi-ширина
струи, li-длина
клетки.
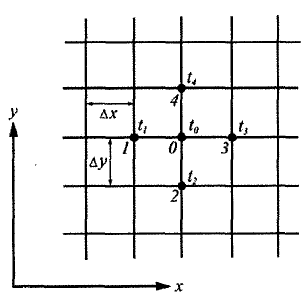 етод
релаксации предусматривает замену
дифференциалов в уравнении стационарной
теплопроводности конечными разностями.
При такой замене дифференциальное
уравнение примет вид д^2t/дх^2
+ д^2t/дх^2
=0. Заключается в достижении равновесного
состояния поля. Разбиваем сетку на
квадраты. дх = дy.
Ведем несколько узлов (1,2,3) и у них в
этих точках будет соответ. температура
. Мы должны найти тем-ру в каждом узле
этой сетки.
етод
релаксации предусматривает замену
дифференциалов в уравнении стационарной
теплопроводности конечными разностями.
При такой замене дифференциальное
уравнение примет вид д^2t/дх^2
+ д^2t/дх^2
=0. Заключается в достижении равновесного
состояния поля. Разбиваем сетку на
квадраты. дх = дy.
Ведем несколько узлов (1,2,3) и у них в
этих точках будет соответ. температура
. Мы должны найти тем-ру в каждом узле
этой сетки.