Тема: Вычисление определенного интеграла и применение определенного интеграла к решению задач Продолжительность занятия:

- специальность 230103 Автоматизированные системы обработки информации и управление в промышленности – 2 часа

- специальность 151001 Технология машиностроения - 2 часа

- специальность 260704 Технология текстильных изделий – 1 час

- специальность 140212 Электроснабжение промышленных предприятий - 2 часа

- специальность 080110 Экономика и бухгалтерский учет в промышленности- 4 часа

Цель занятия. Научить студента вычислять определенные интегралы и применять их к решению задач.

Порядок проведения:

1. изучить теоретический материал;

2. разобрать предложенный пример;

3. выполнить самостоятельно индивидуальные задания;

4. ответить на контрольные вопросы.

Студент должен:

знать:формулу Ньютона-Лейбница, формулы интегрирования заменой переменной и по частям для определенного интеграла и применения определенного интеграла к решению задач;

уметь:вычислять определенные интегралы методом замены переменного и по частям и применять определенные интегралы для решения задач.

1. Понятие определённого интеграла

Пусть функция определена на отрезке. Выполним следующие действия.

1. С помощью точекразобьём отрезокнаnчастичных отрезков.

2. В каждом частичном отрезке ,i=1,2,…,nвыберем произвольно точкуи вычислим значение функции в ней, т.е. величину.

3. Умножим найденное значение функции на длинусоответствующего частичного отрезка:.

4. Составим сумму S_nуказанных произведений:

.

Сумма вида называется интегральной суммой функциина отрезке.

Обозначим через длину наибольшего частичного отрезка:.

5. Найдём предел интегральной суммы, при так, что.

Если при этом интегральная сумма S_nимеет пределI, который не зависит ни от способа разбиения отрезкана частичные отрезки, ни от выбора точек в них, то числоIназывается определённым интегралом от функциина отрезкеи обозначается. Таким образом,.

Числа иназываются соответственно нижним и верхним пределами интегрирования,– подынтегральной функцией,– подынтегральным выражением,– переменной интегрирования, отрезок- областью (отрезком) интегрирования.

Функция , для которой на отрезкесуществует определённый интеграл, называется интегрируемой на этом отрезке.

Основные свойства определённого интеграла

1. , где с – число

2.

Свойство 2 справедливо для любого конечного числа слагаемых.

3.

4. , гдеa<c<b

Свойство 4 позволяет разбивать отрезок интегрирования на части. Свойство 4 называют аддитивностью определённого интеграла. Свойство применяют при вычислении площадей фигур.

Определённый интеграл применяют для решения геометрических и физических задач. Например, вычисление площадей фигур, объёмов тел вращения, работы переменной силы, расстояния при прямолинейном перемещении, длины дуги плоской кривой, объёма тел, площади поверхности вращения, статических моментов и координат центра тяжести плоской кривой и многие другие прикладные задачи.

2. Вычисление определённого интеграла.

Для вычисления определённого интеграла от функции f(x) на отрезкеприменяют формулу Ньютона-Лейбница:

,

т.о. для вычисления определённого интеграла надо найти соответствующий неопределённый интеграл, а затем вычислить разность значений первообразной при верхнем и нижнем пределах интегрирования.

Формулу Ньютона-Лейбница также записывают в виде:

Пример 2.1.Вычислить.

Найдём одну из первообразных для функции

, т.е.

Тогда по формуле Ньютона-Лейбница

Решение записывают в виде:

Пример 2.2.Вычислить

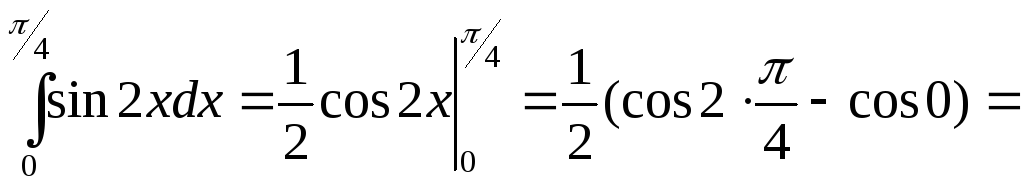
Пример 2.3.Вычислить

.