|
|
|
3 |
t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 11cos |
|
|
0 t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 11sin3 t |
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, |
ограниченной линиями: y2 2x, |
x2 y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
dx |
|
|
0 |
|
dx |
|
4. |
Исследовать сходимость интегралов: а) |
|
|
; |
б) |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
3 1 x3 |
3 x2 2x 1 |
|
|
Вариант №2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
e x dx |
|
|
|
|
|
|
|
|
|
1. |
Вычислить несобственный интеграл |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Вычислить площадь фигуры, ограниченной линиями: y x2 , |
y 3 2x . |
3. |
Вычислить площадь фигуры, ограниченной линией: 2 |
a3 cos 2 . |
|
4. |
Вычислить длину дуги кривой y ln sin x на отрезке |
x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
Факультет автоматики и вычислительной техники
Тест «Простейшие приемы интегрирования» (5-10 баллов)
1. sin x dx
ecos x
2. arccos(x / 2) dx
 4 x2
4 x2
3. e2x2 ln xdx
4. cos x dx  x
x
dx
5. x sin2 (1 ln x)
6. 3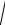 1 log2 x dx x
1 log2 x dx x
Контрольная работа «Неопределенный интеграл» (15-20 баллов)
Вариант №1
dx
1. x ln2 x
xdx
2. cos2 x
3. x4 1 dx x4 1
4. sin3 x dx  cos x
cos x
dx
5. 2 sin x
Вариант №2
2.
 x ln x dx
x ln x dx
xdx
3.cos2 x
x
4. dx
1 4 x3
x3
dx
5. 1 sin x cos x
dx
6. cos4 x sin2 x
Контрольная работа «Определенный интеграл» (10-15 баллов)
Вариант №1
1. Вычислить длину дуги кривой, заданной уравнением:
|
|
y |
x2 |
|
ln x |
1 x 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
2. |
Найти площадь фигуры, ограниченной кривой a sin 3 . |
|
3. |
Вычислить объем тела вращения фигуры, ограниченной линиями |
|
|
y 2x x2 , |
y x 2 , |
|
|
|
|
|
вокруг оси ОХ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
dx |
|
4. |
Вычислить интеграл или установить его расходимость: |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 (3 x)2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Исследовать несобственный интеграл на сходимость: |
1 |
|
arctg x dx . |
|
|
|
|
|
|
|
|
1 x |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вариант №2 |
|
|
|
1. |
Вычислить несобственные интегралы: |
|
|
|
|
|
|
1 |
3x |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
а) |
|
|
dx ; |
б) e2xdx . |
|
|
|
|
|
|
|
|
|
3 x2 |
|
|
1 |
|
|
|
|
|
|
|
|
0 |
|
|
2. |
Исследовать несобственный интеграл на сходимость |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x2 2x 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 4 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 3(2 cos t cos 2t), |
от t 0 до t 2 . |
3. |
Найти длину дуги кривой |
|
|
|
3(2sin t sin 2t) |
|
|
|
|
|
y |
|
|
4. |
Найти площадь фигуры, ограниченной линиями sin , |
2sin . |
Факультет экономики и управления
Тест «Интегрирование путем подведения функции под знак дифференциала» (5-10 баллов)
|
Вариант №1 |
Вариант №2 |
|
|
|
|
|
|
|
|
|
1. |
|
1 ln x |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
1 4sin x cos x dx |
x |
|
|
|
|
|
|
|
|
|
2. |
|
|
dx |
|
2. |
|
|
x3 x |
|
dx |
|
x(2 ln2 x 5) |
|
x4 1 |
|
|
|
|
|
|
|
|
|
|
3. e2 cos 3x sin 3x dx |
3. |
|
|
arcsin2 x 1 |
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
|
tg 2x |
dx |
|
|
|
|
|
|
|
|
|
x dx |
|
|
|
|
|
|
cos2 2x |
4. |
|
|
|
|
|
|
|
|
|
(x 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Контрольная работа «Неопределенный интеграл» (15-20 баллов)
Вариант №1
2.(x 9) sin x dx
xdx
3.(x2 4)(x 2)
5.x 
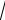 x dx
x dx

 x 3
x 3
|
6. |
|
dx |
|
|
|
|
|
|
3sin x 10 cos x |
|
|
|
7. |
7 5x |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
x2 6 |
|
|
|
|
|
Вариант №2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
|
|
|
e5x |
|
|
|
dx |
|
|
|
|
|
|
|
|
3 e5x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 cos2 x |
2sin2 x 3sin 2x |
|
|
|
|
|
3. |
|
|
x 9 |
|
dx |
|
|
|
|
|
|
|
|
x3 9x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
|
ln x |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x6 |
|
2x 6 x5 |
|
|
|
|
x |
|
|
|
|
|
|
|
101 x |
|
|
|
|
3 |
|
x |
|
|
|
6. |
cos |
|
|
sin |
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
7. |
x cos(3x2 |
5) dx |
Контрольная или домашняя работа «Определенный интеграл» (5-10 баллов)
|
|
|
|
|
|
Вариант №1 |
|
|
|
|
/ 4 |
dx |
|
|
|
|
|
|
1. |
Вычислить интеграл: |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
sin2 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Вычислить площадь фигуры, ограниченной линиями: |
|
|
|
y x2 2x 3, |
y 3x 1. |
3. |
Вычислить объем тела, образованного вращением вокруг оси ОХ фигуры, |
ограниченной линиями: |
y x3, |
x 0, |
y 8. |
|
|
4. |
Исследовать несобственные интегралы на сходимость: |
|
|
|
1 |
dx |
|
|
dx |
|
|
|
а) |
; |
б) |
. |
|
|
|
|
|
|
|
|
|
|
0 x3 3x2 |
|
e |
x ln x |



 4
4 
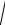 1 log
1 log
 cos
cos 
 x
x 



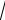 x
x 
 x
x 