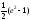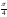Int / Таблица интегралов
.docxТаблица интегралов
-
Непосредственное интегрирование
-
-
Внесение под знак дифференциала
-
-
Интегрирование заменой переменной
-
-
Интегрирование по частям
-
-
Метод неопределенных коэффициентов
-
-
Интегрирование триг. функций
-

-

-
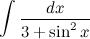
-

-

-

-

-

-

-

-
 универс.тригонометрич.замена
универс.тригонометрич.замена -
-
мм
-
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
-
2)Вычислить определенный интеграл с помощью формулы Ньютона-Лейбница:
-
-
1.
 .
.
-
2.
 .
.
-
3.
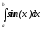 .
.
-
4.
 .
.
-
5.
 .
.
-
6.
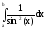 .
.
-
7.
 .
.
-
8.
 .
.
-
9.
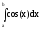 .
.
-
10.
 .
.
-
-
-
11.
 .
.
-
12.
 .
.
-
13.
 .
.
-
14.
 .
.
-
15.
 .
.
-
16.
 .
.
-
17.
 .
.
-
18.
 .
.
-
19.
 .
.
-
20.
 .
.
-
-
3. С помощью подходящих подстановок вычислить интегралы
-
1.
 .
.
-
2.
 .
.
-
3.
 .
.
-
4.
 .
.
-
5.
 .
.
-
6.

-
7.

-
8.

-
9.

-
10.

-
-
4. С помощью формулы интегрирования по частям вычислить интегралы
-
1.
 .
.
-
2.
 .
.
-
3.
 .
.
-
4.
 .
.
-
5.
 .
.
-
6.
 .
.
-
7.
 .
.
-
8.
 .
.
-
9.
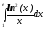 .
.
-
10.
 .
.
-
-
***2. Вычисление определённого интеграла.
-
Пример 2.1. Вычислить
 .
. -
Пример 2.2. Вычислить

-
Пример 2.3. Вычислить

-
Задания
-
Ответы
-
1.

-
256
-
2.

-
3.

-
4.

-
5.

-
6.

-
-
-
методом подстановки:
-
Пример 2.4. Вычислить

-
Пример 2.5. Вычислить

-
Задания
-
Ответы
-
1.

-
2.
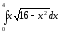
-
3.

-
4.

-
5.

-
-
-
методом по частям применяют формулу

-
Пример 2.6. Вычислить

-
Пример 2.7. Вычислить
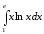
-
-
-
Задания
-
Ответы
-
1.
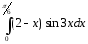
-
2.

-
3.

-
4.

-
5.

-
-
-
3. Вычисление площадей плоских фигур***
-
-

-

-
Пример 3.1. Вычислить площадь фигуры, ограниченной линиями
 ,
,
 ,
,
 ,
,
 .
. -
Построим линии, ограничивающие фигуру.
-
 –
парабола, симметричная относительно
оси оу, вершина (0;1).
–
парабола, симметричная относительно
оси оу, вершина (0;1). -
 – прямая, проходящая через точку (2;0),
параллельная оси оу.
– прямая, проходящая через точку (2;0),
параллельная оси оу. -
 – аналитическое выражение оси ох.
– аналитическое выражение оси ох. -
 – аналитическое выражение оси оу.
– аналитическое выражение оси оу. -

-
Рис. 7.
-
Построенная фигура (рис.7) является криволинейной трапецией с основанием на оси ох, поэтому её площадь вычисляется по формуле
-
 .
. -
 ,
,
 ,
,
 .
.
-
Тогда
 (кв. ед.).
(кв. ед.).-
Вычислить площадь фигуры, ограниченной линиями:
-
Ответы
-
1.

-
 ед2
ед2
-
2.
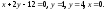
-
21 ед2
-
3.

-
 ед2
ед2
-
4.

-
18 ед2
-
5.

-
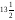 ед2
ед2
-
6.
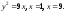
-
104 ед2
-
7.

-
 ед2
ед2
-
8.

-
 ед2
ед2
-
9.

-
 ед2
ед2
-
10.

-
 ед2
ед2
-
11.

-
 ед2
ед2
-
12.

-
 ед2
ед2
-
13.

-
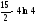 ед2
ед2
-
14.

-
4,25 ед2
-
15.

-
 ед2
ед2
-