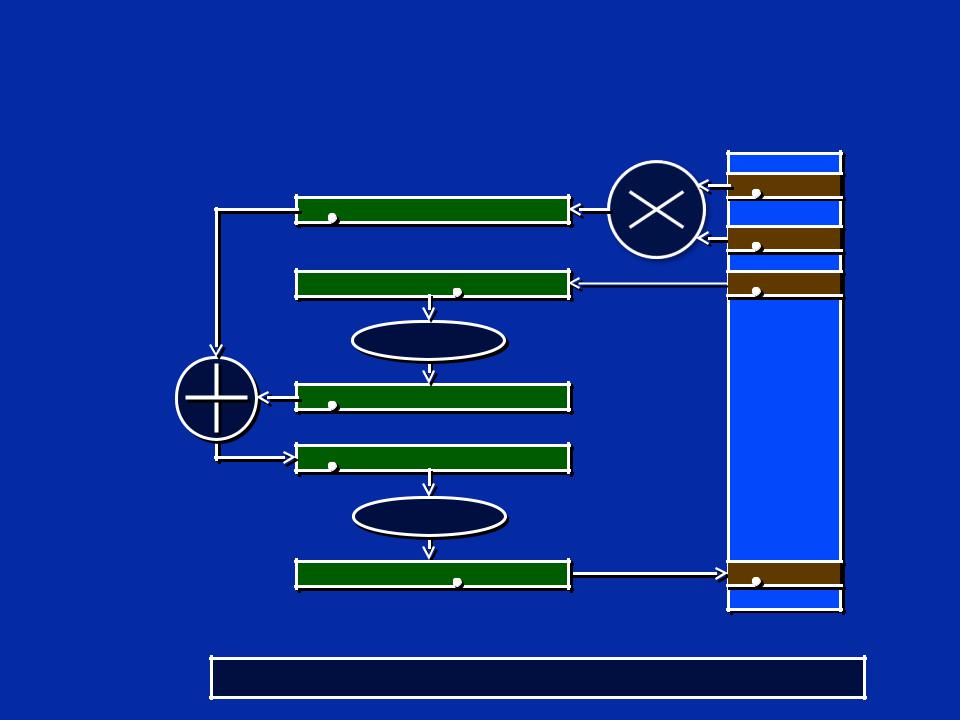
Традиционный 16 битный подход в
“Q” арифметике y = mx + b
|
|
|
s |
Q15 |
ss |
Q30 |
|
|
|
|
|
|
s |
Q15 |
sssssssssssss |
Q15 |
s |
Q15 |
|
|
<< 15 |
Выравнивание |
|
|
|
точки в десятичной |
|
|
|
|
|
дроби для сложения |
|
|
ss |
Q30 |
|
|
|
sI |
Q30 |
|
|
|
|
>> 15 |
Выравнивание |
|
|
|
точка в десятичнойс |
|
|
|
|
дроби для сохранения |
|
||
ssssssssssssI |
Q15 |
s |
Q15 |
|
M
X
B
Y
в C:: |
Y = ((i32) M * (i32) X + (i32) B << Q) >> Q; |
11 - 21 |
|
|
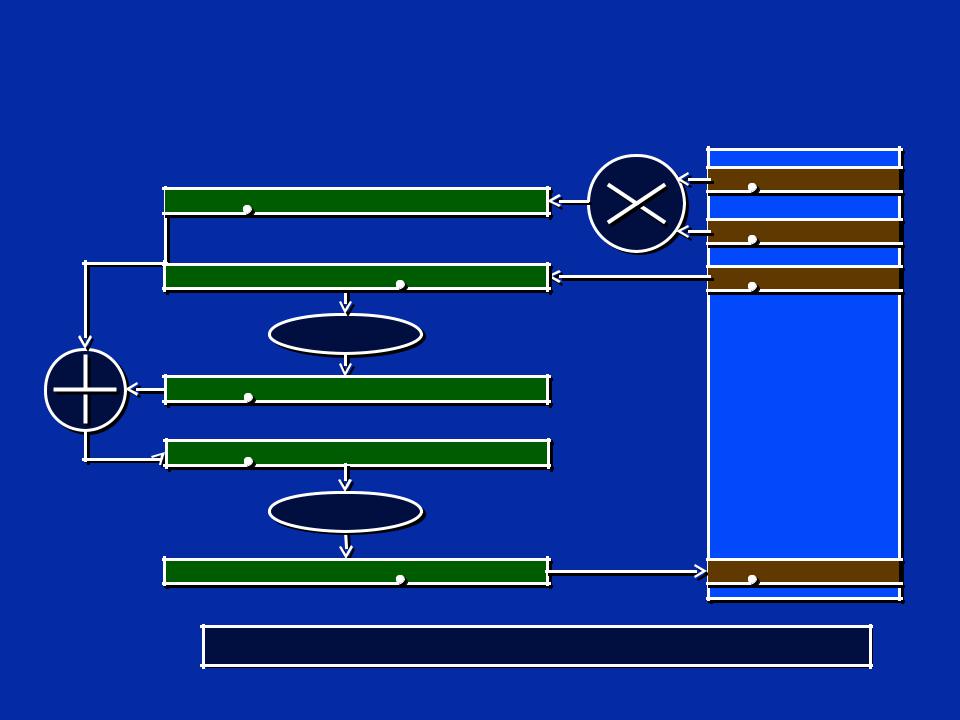
Традиционный 32 битный подход в “Q” арифметике
y = mx + b
|
|
|
I8 |
Q24 |
I16 |
Q48 |
|
|
|
|
|
|
I8 |
Q24 |
ssssssssssssssssssI8 |
Q24 |
I8 |
Q24 |
|
|
<< 24 |
Выравнивание |
|
|
|
точки в десятичной |
|
|
|
|
|
дроби для сложения |
|
|
ssssI8 |
Q48 |
|
|
|
I16 |
Q48 |
Выравнивание |
|
|
|
>> 24 |
|
|
|
|
точки в десятичной |
|
|
|
|
|
дроби для сохранения |
|
|
sssssssssssssssssI16 |
Q24 |
I8 |
Q24 |
|
M
X
B
Y
в C:: |
Y = ((i64) M * (i64) X + (i64) B << Q) >> Q; |
Замечание:: требуется поддержка 64--битного типа данных компилятором11 - 22
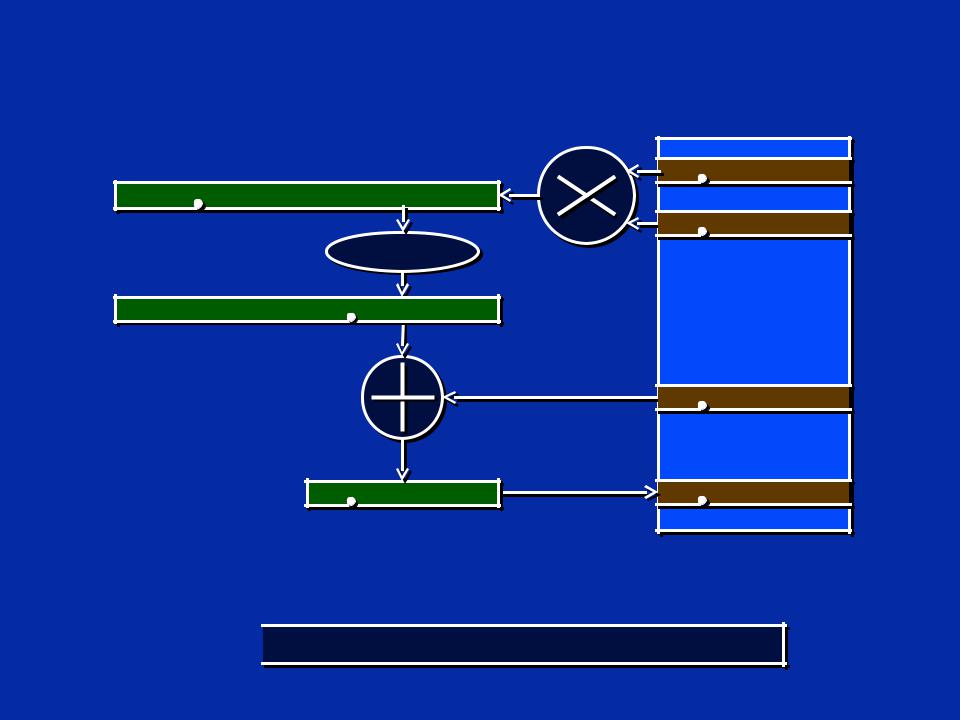
32-битный подход IQmath y = mx + b
|
|
|
I8 |
Q24 |
I16 |
Q48 |
|
|
|
Выравнивание |
>> 24 |
I8 |
Q24 |
|
точки в десятичной |
|
|
||
дроби для умножения |
|
|
||
sssssssssssssssssI16 |
Q24 |
|
|
|
I8 Q24
I8 |
Q24 |
I8 |
Q24 |
M X
B
Y
в C::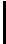 
Y = ((i64) M * (i64) X) >> Q + B;
11 - 23
Подход Iqmath - Операция
умножения
Y = ((i64) M * (i64) X) >> Q + B;
Переопеределение операции умножения следующим образом:
_IQmpy(M,X) == ((i64) M * (i64) X) >> Q
Похоже на исходное выражение:
Y = _IQmpy(M,X) + B;
C28x компилятор поддерживает “_IQmpy” инструкцию; генерируя ассемблерный код:
MOVL |
XT,@M |
|
|
|
|
IMPYL |
P,XT,@X |
; P = |
младшие |
32-бита M*X |
|
QMPYL |
ACC,XT,@X |
; ACC = |
старшие |
32-бита M*X |
|
LSL64 |
ACC:P,#(32-Q) ; ACC = |
ACC:P << |
32-Q |
||
|
|
; ( P = |
ACC:P >> |
Q) |
|
ADDL |
ACC,@B |
; Добавление B |
MOVL |
@Y,ACC |
; Результат Y = _IQmpy(M*X) + B |
|
|
; 7 Cycles |
11 - 24
Подход IQmath похож на
плавающую точку!
Плавающая
точка
Традиционно
в
фиксированн ой точке “IQmath”I
в C
“IQmath”I
в C++
float Y, M, X, B;
Y = M * X + B; long Y, M, X, B;
Y = ((i64) M * (i64) X + (i64) B << Q)) >> Q; _iq Y, M, X, B;
Y = _IQmpy(M, X) + B;
iq Y, M, X, B;
Y = M * X + B;
Достоинство в переводе операторов на языке C+ +,
запись “IQmath” похожа на плавающую точку11 - 25
(более натурально!)
Подход IQmath - GLOBAL_Q
Пользователь выбирает значение “Global Q” для всего приложения
GLOBAL_Q
Базируясь на требованиях к динамическому диапазону или точности, на пример:
GLOBAL_Q |
|
Максимальное |
|
Минимальное |
|
|
Разрешение |
|||||
|
значение |
|
|
значение |
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
28 |
|
7.999 |
999 |
996 |
|
-8.000 |
000 |
000 |
|
0.000 |
000 |
004 |
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
127.999 |
999 |
94 |
|
-128.000 |
000 |
00 |
|
0.000 |
000 |
06 |
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
2047.999 |
999 |
|
|
-2048.000 |
000 |
|
|
0.000 |
001 |
|
#define GLOBAL_Q 18 |
// |
задано в файле |
“IQmathLib.h” |
|
_iq |
Y, M, X, B; |
|
|
|
Y = |
_IQmpy(M,X) + B; |
// |
все значения в |
формате Q = 18 |
Пользователь может отдельно определить Q значение:
_iq20 Y, M, X, B;
Y = _IQ20mpy(M,X) + B; // все значения в формате Q = 20
11 - 26
Подход IQmath - выбор
фиксированной точки или плавающей точки
Y = _IQmpy(M, X) + B;
Пользователь выбирает арифметику ((в “IQmathLibI t ib..h” файле))
#if MATH_TYPE == IQ_MATH
#if MATH_TYPE == FLOAT_MATH
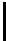Y = (float)M * (float)X + (float)B;
Компиляция & запуск используя “IQmath” на C28x
Компиляция & Запуск используя арифметику плавающей точки на C3x, C67x,C28x (RTS), PC,..
Все “IQmath”I |
операторы имеют |
|
эквивалентные операции в плавающей точке |
11 - 27 |
|
Библиотека IQmath: математические
и тригонометрические функции (v1.4)
Операци |
Плавающая |
“IQmath” в C |
|
“IQmath” в |
|||||||||
|
точка |
|
|
||||||||||
я |
float A, B; |
|
|
_iq A, B; |
|
|
C++ |
|
|
||||
тип |
|
|
|
iq A, B; |
|||||||||
констан |
A = 1.2345 |
|
A = _IQ(1.2345) |
|
A = IQ(1.2345) |
|
|||||||
ты |
|
A * B |
|
|
_IQmpy(A , B) |
|
|
A * B |
|
|
|||
умножен |
|
|
|
|
|
|
|
||||||
ие |
|
A / B |
|
|
|
_IQdiv (A , B) |
|
|
A / B |
|
|
||
делени |
|
|
|
|
|
|
|
|
|||||
е |
|
A + B |
|
|
|
A + B |
|
|
A + B |
|
|
||
сложен |
|
|
|
|
|
|
|
|
|||||
ие |
|
A - B |
|
|
|
|
A - B |
|
|
A – B |
|
|
|
вычитани |
|
|
|
|
|
|
|
|
|
||||
булевы |
, , |
, ||, |
, | |
, , |
, |
, , |
, |
, | , , || |
, |
, |
, ||, |
, | , , |
|
е |
>, >=, <, <=, ==, |=, &&, |
>, >=, <, <=, ==, |=, &&, || |
>, >=, <, <=, ==, |=, &&, |
|
|||||||||
е |
|
|| |
|
|
|
|
|
|
|
|
|| |
|
|
тригономе |
sin(A),cos(A) |
|
_IQsin(A),_IQcos(A) |
|
IQsin(A),IQcos(A) |
||||||||
- |
i |
, |
|
|
I |
i |
, |
I |
|
I i |
,I |
|
|
sin(A*2pi),cos(A*2pi) |
_IQsinPU(A),_IQcosPU(A) |
IQsinPU(A),IQcosPU(A) |
|||||||||||
трические |
i |
i , |
|
i) |
I i |
, |
I |
I |
i |
,I |
|
|
|
функции |
atan(A),atan2(A,B) |
_IQatan(A),_IQatan2(A,B) |
IQatan(A),IQatan2(A,B) |
||||||||||
|
|
, |
|
, |
I |
|
, I |
, |
I |
|
,I |
, |
|
|
atan2(A,B)/2pi |
_IQatan2PU(A,B) |
|
IQatan2PU(A,B) |
|||||||||
|
|
, |
/ |
i |
|
I |
|
, |
|
I |
|
, |
|
|
sqrt(A),1/sqrt(A) |
_IQsqrt(A),_IQisqrt(A) |
IQsqrt(A),IQisqrt(A) |
||||||||||
|
|
, / |
|
|
I |
|
, |
I i |
|
I |
,I |
i |
|
|
sqrt(A*A + B*B) |
|
_IQmag(A,B) |
|
IQmag(A,B) |
||||||||
|
|
|
|
|
|
I |
|
, |
|
I |
|
, |
|
насыщен |
if(A > Pos) A = |
|
_IQsat(A,Pos,Neg) |
IQsat(A,Pos,Neg) |
|||||||||
ие |
Pos |
|
|
|
|||||||||
|
if(A < Neg) A = |
|
|
|
|
|
|
|
|
|
|||
|
Neg |
|
|
|
|
приблизительно от ~28 до ~31 бита |
|||||||
Точность функций/операций/ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
11 - 28 |
|
Библиотека IQmath:
функции преобразования (v1.4)
Операци |
Плавающая |
“IQmath” в C |
“IQmath” в |
|
и |
точка |
|
_IQtoIQN(A) |
C++ |
iq to iqN |
A |
|
IQtoIQN(A) |
|
iqN to iq |
A |
|
_IQNtoIQ(A) |
IQNtoIQ(A) |
integer(iq) |
(long) A |
_IQint(A) |
IQint(A) |
|
fraction(iq |
A – (long) A |
_IQfrac(A) |
IQfrac(A) |
|
iq)= |
A * (float) B |
_IQmpyI32(A,B) |
IQmpyI32(A,B) |
|
iq*long |
(long) (A * (float) |
_IQmpyI32int(A, |
IQmpyI32int(A,B |
|
integer(iq*lon |
||||
g) |
B) |
|
B) |
) |
fraction(iq*lon |
A - (long)(A*(float) |
_IQmpyI32frac(A, |
IQmpyI32frac(A,B |
|
g) |
B) |
|
B) |
) |
qN to iq |
A |
|
_QNtoIQ(A) |
QNtoIQ(A) |
iq to qN |
A |
|
_IQtoQN(A) |
IQtoQN(A) |
string to iq |
atof(char) |
_atoIQ(char) |
atoIQ(char) |
|
IQ to float |
A |
|
_IQtoF(A) |
IQtoF(A) |
IQmath.lib |
> библиотека математических |
|||
I |
th.lib |
|
|
|
функций
IQmathLibI t ib..h > заголовочный файл для C
IQmathCPPI t ..h > заголовочный файл для C++
11 - 29
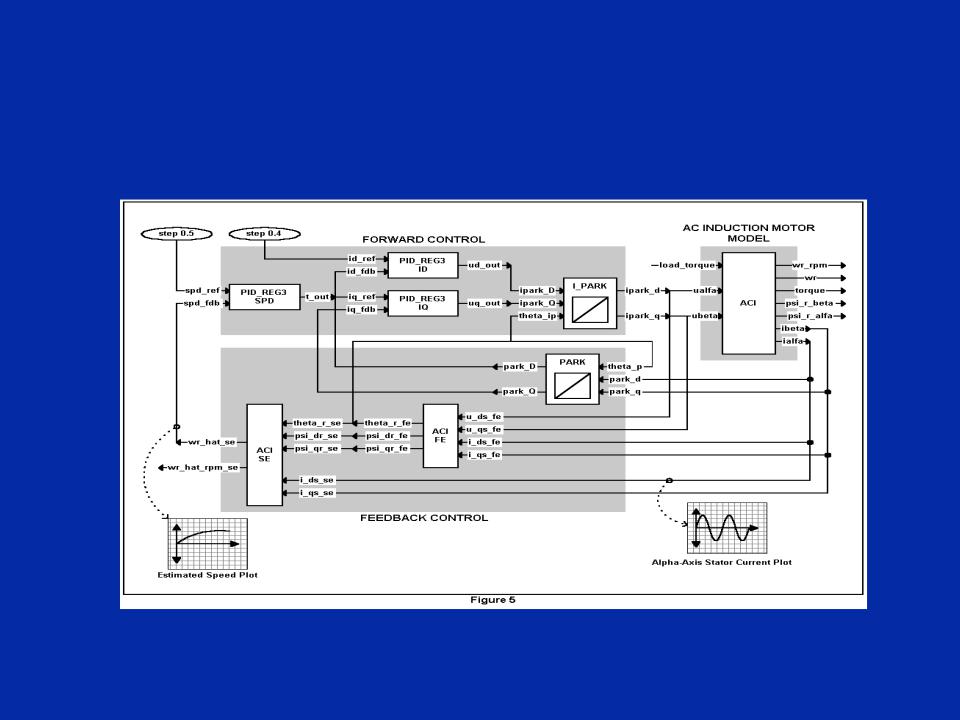
Пример управления асинхронным
электродвигателем переменного тока
Один из сложнейших алгоритмов управления двигателем
Безсенсорное управление прямым магнитным потоком
асинхронным двигателем переменного тока
Цель: оценить скорость вращения двигателя и определить первоначальный ток статора 11 - 30