Модуль 11: Библиотека IQ – Math C28x
Цифровой сигнальный контроллер TMS320F2812
Texas Instruments Incorporated
Плавающая точка, целочисленная и
фиксированная точка
Две основных категории процессоров:
Плавающей точкой
Целочисленной/фиксированной точкой
В чем отличие?
В чем преимущество и недостатки ?
Управление в реальном времени : фиксированная точка !
Обсуждение ограничений при разработке в арифметике фиксированной точки
Сравнение / отличие плавающей точки
иIQ представления
Подход Texas Instruments - IQ-Math 11 - 2
Типы процессоров
Процессоры с плавающей точкой
Модули внутренней аппаратуры
поддерживают операции с плавающей точкой
Примеры:серия Intel’s Pentium,
Texas Instruments C 6000 DSP
Большой динамический диапазон для числовых вычислений
Достаточно дорогостоящие
Процессоры с фиксированной точкой
Арифметический модуль с фиксированной точкой
Большинство встраиваемый контроллеров имеют устройства с фиксированной точкой
Например: Motorola HC68x, Infineon C166,
Texas Instruments TMS430, TMS320C5000, 11 - 3
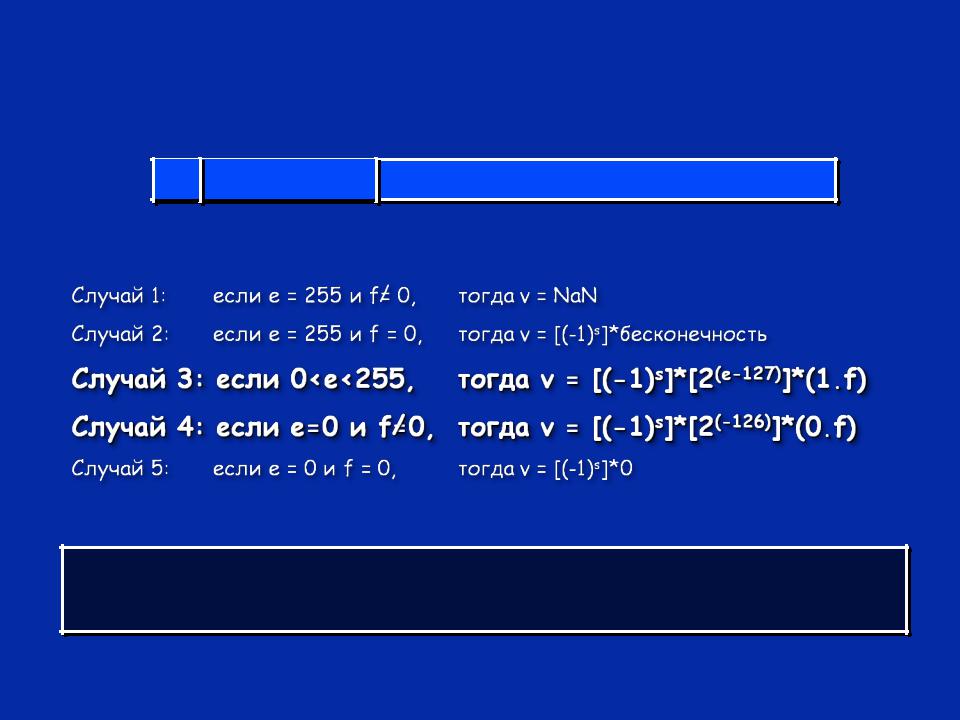
IEEE стандарт 754 плавающей точки с одинарной точностью
31 30 |
23 22 |
0 |
s eeeeeeee fffffffffffffffffffffff
Знак -- 1 битЭкспонента -- 8 бит Мантисса ((дробная часть)) -- 23 бита
Достоинство Экспонента дает большой динамический диапазон Недостаток Точность чисел зависит от экспоненты
11 - 4
Плавающая точка не решает всего!
Пример: x = |
10.0 |
(0x41200000) |
+ y = |
0.000000238(0x347F8CF1) |
|
z = 10.000000238Неправильно!
Не возможно представить 10.000000238 в плавающей точке с одинарной точностью
0x412000000 |
= |
10.000000000 |
не может быть |
0x412000001 |
= |
10.000000238 |
|
10.000000950 |
представлен! |
Таким образом z округляется к 10.000000000
11 - 5
Основы целочисленной системы
исчисленияДвоичные числа
01102 |
= (0*8)+(1*4)+(1*2)+(0*1) |
= 610 |
301111010 2 |
= (1*16)+(1*8)+(1*4)+(1*2)+(0*1) = |
|
Числа в дополнительном коде
01102 |
= (0*-8)+(1*4)+(1*2)+(0*1) |
= 610 |
-210111102 |
= (1*-16)+(1*8)+(1*4)+(1*2)+(0*1) = |
|
11 - 6
Умножение четырех битных целых
чисел
0100 x 1101 00000100
0000000
000100
11100
11110100
Аккумулятор
11110100 
Память данных ?
Имеется ли другая систем исчисления?11 - 7
Да: двоичные дроби
1 |
• |
0 |
1 |
1 |
|
|
|
|
|
-1 |
1/2 |
1/4 |
1/8 |
= -1 + 1/4 + 1/8 = -5/8
Дроби обладают такой особенностью дробь x дробь = дробь
11 - 8
Четырех битное умножение
0100
.
x 1101
.
00000100
0000000
000100
11100
11110100
Аккумулятор
11110100 
-1/4
11 - 9
Дробное представление
31 |
|
0 |
S IIIIIIII |
fffffffffffffffffffffff |
|
|
|
32 битная мантисса |
-2I + 2I-1 + … + 21 + 20 . 2-1 + 2-2 + … |
||
+ 2-Q |
“IQ” – формат |
|
|
||
|
“I” ЦЕЛАЯ часть дроби |
|
|
“Q” |
дробная часть дроби |
Достоинство Точность одинакова для всех чисе
в IQ формате
Недостатки Ограниченный динамический диап
по сравнению с плавающей точко
10