Лекция 5: Волновая оптика

Оптика световых пучков Оптические резонаторы

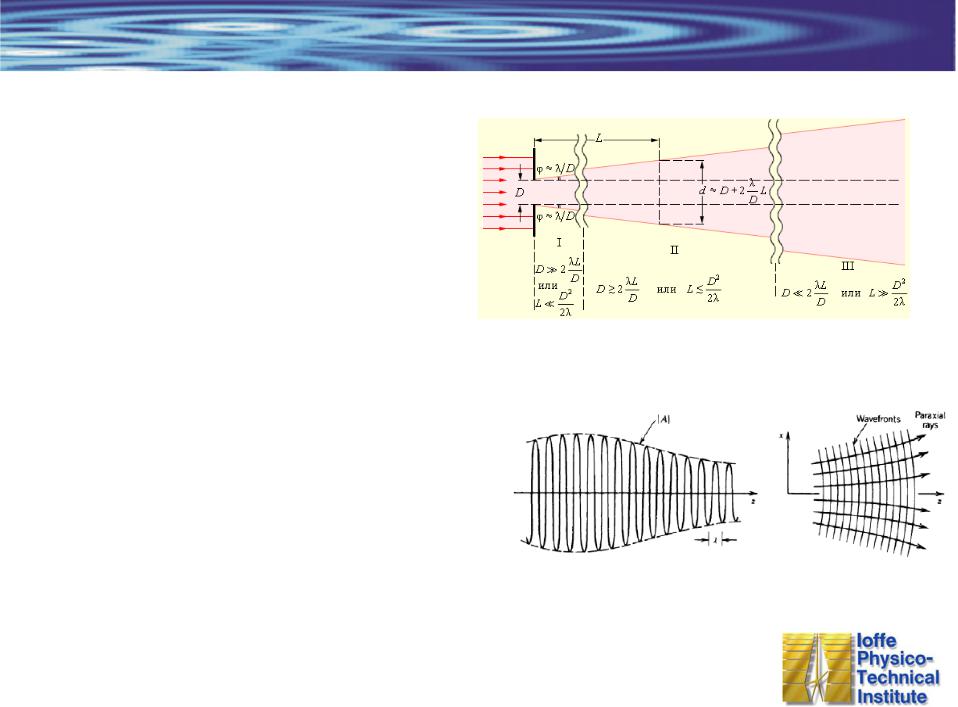
Оптические пучки

По законам волновой оптики любой

световой пучок расходится –

дифракционная расходимость.

Причем чем меньше диаметр, тем быстрее.

Плоская волна – бесконечна в пространстве,

но нет расходимости.

Сферическая волна – точечный источник и

максимальная расходимость.

Параксиальное приближение – оптический пучок

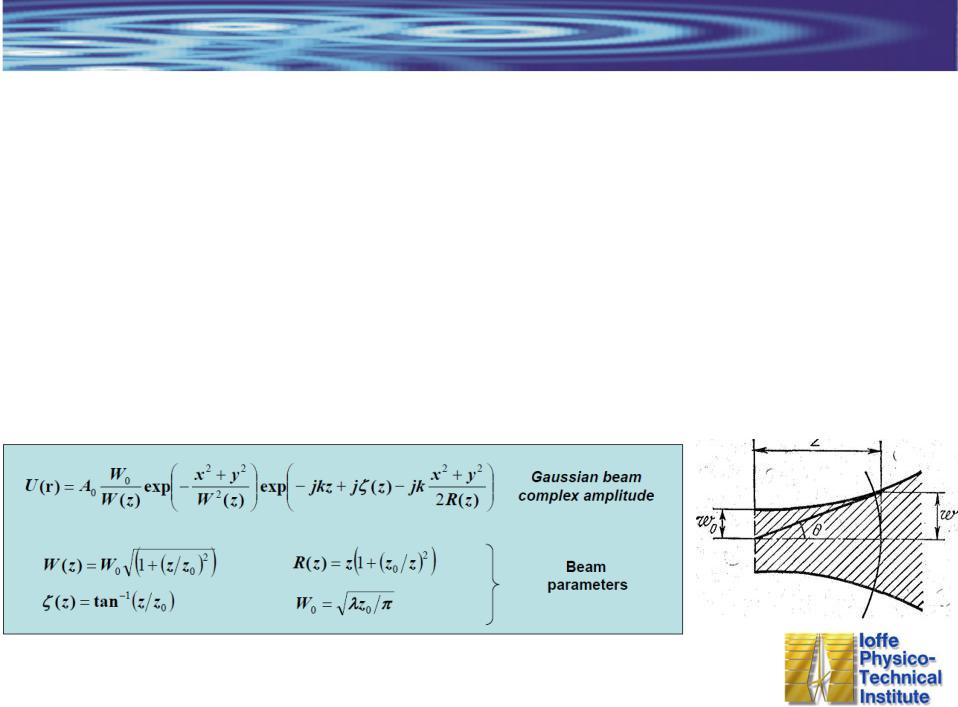
Гауссов пучок

(излучение лазера)

Сферическая волна в параксиальном приближении дает параболическую волну, Гауссов пучок другое решение с квадратичной зависимость фазового фронта.

R(L)

Параметры A0= A1/jz0 и z0 определяются из граничных условий

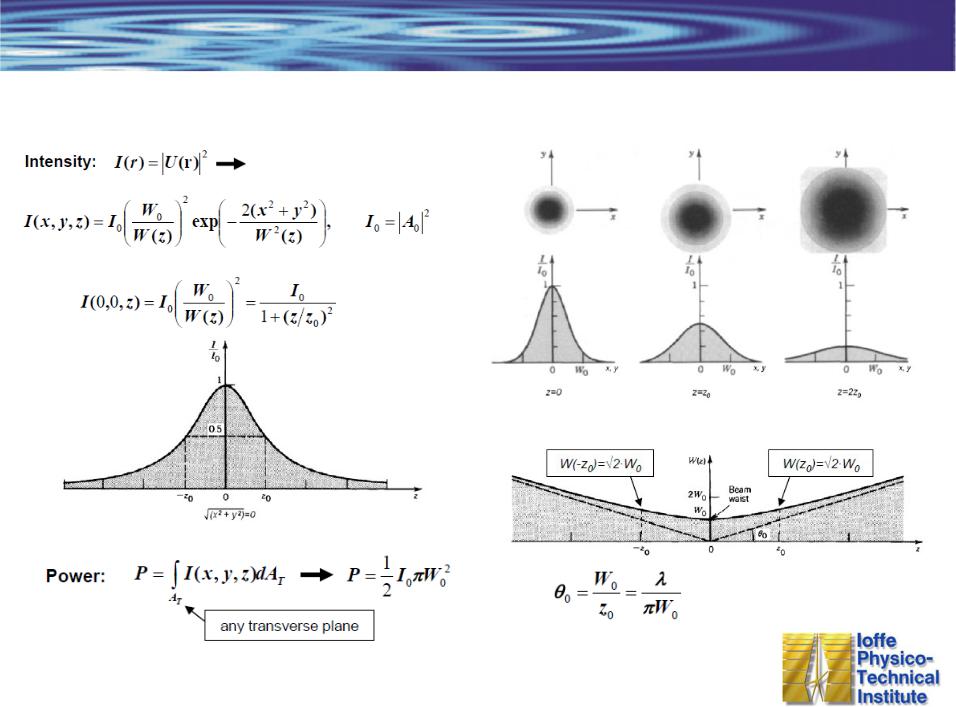
Свойства Гауссова пучка

Интенсивность

Функция Гаусса

Расходимость

Мощность

асимптота при

В круге диаметром W(z) сосредоточено 86% мощности

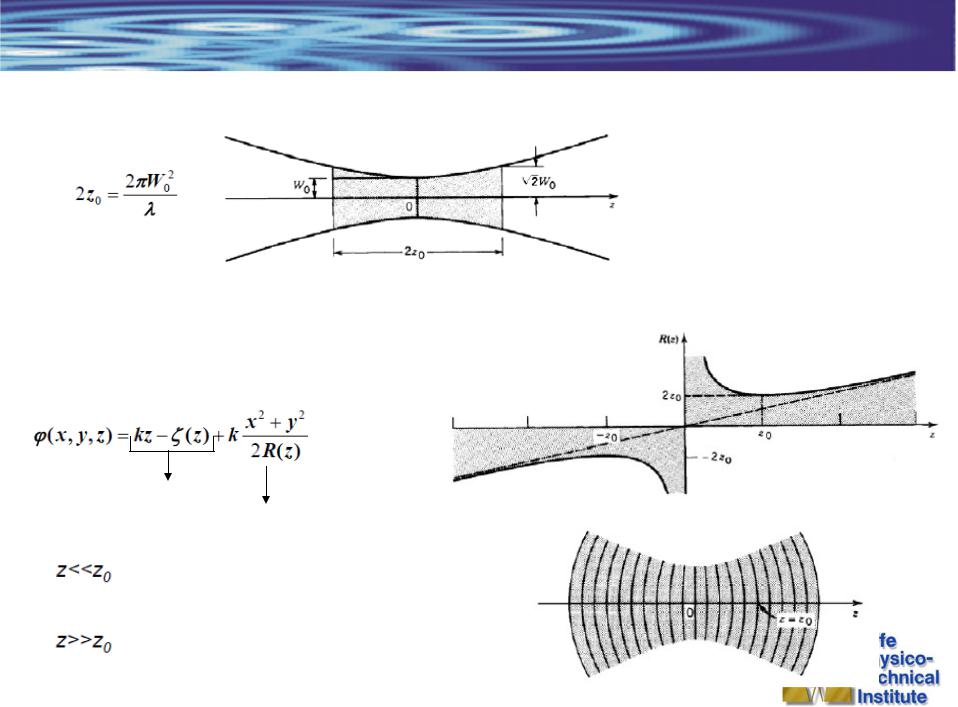
Свойства Гауссова пучка

Глубина фокуса

Для He-Ne лазера (633 нм) размер пятна 2 см имеет глубину фокуса 1 км, при размере 2 мкм, всего лишь 1 мм

Фаза и волновой фронт

плоская волна

искривление волнового фронта

Гауссов пучок – плоская волна

Гауссов пучок – сферическая волна (R=z)

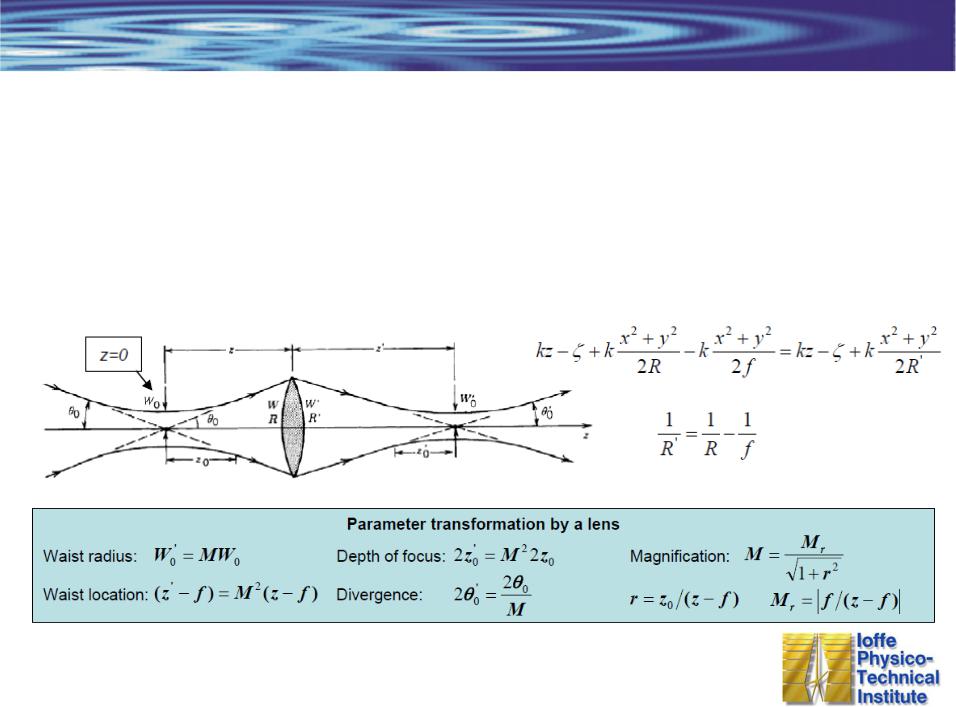
Прохождение Гауссова пучка через оптическую систему

Для системы с осевой симметрией изменяется только размер пятна и радиус кривизны волнового фронта (преобразование Фурье от функции Гаусса – Функция Гаусса)

Тонкая линза

Пропускание пропорционально Изменяется радиус кривизны, размер пятна сохраняется

Уравнение линзы

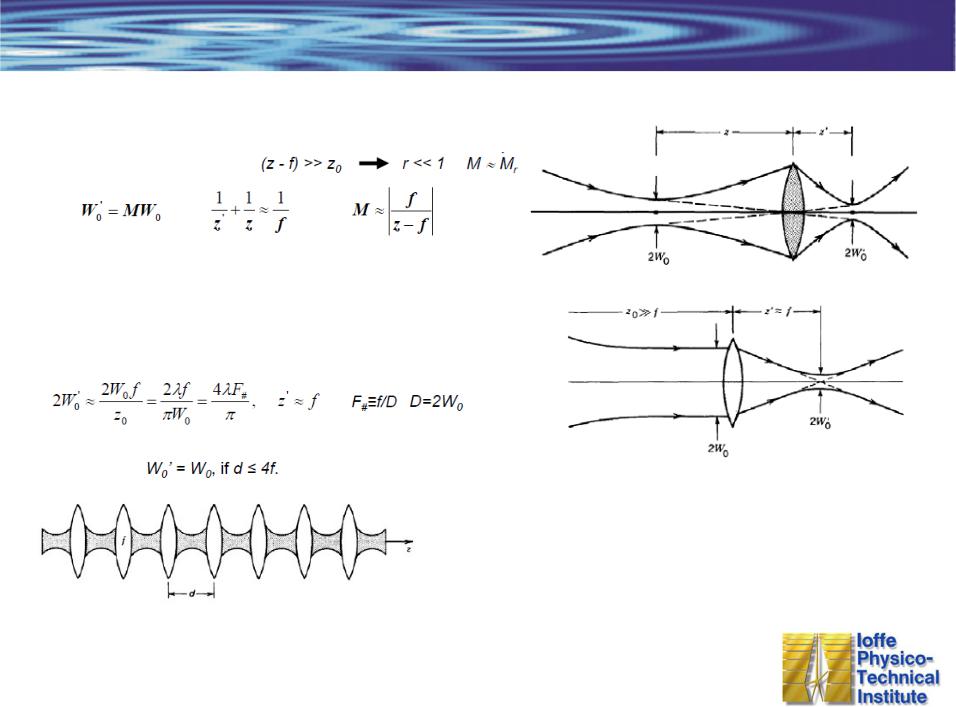
Прохождение Гауссова пучка через оптическую систему

Предел лучевой оптики

Фокусировка

Линза располагается в перетяжке гауссова пучка

Задержка

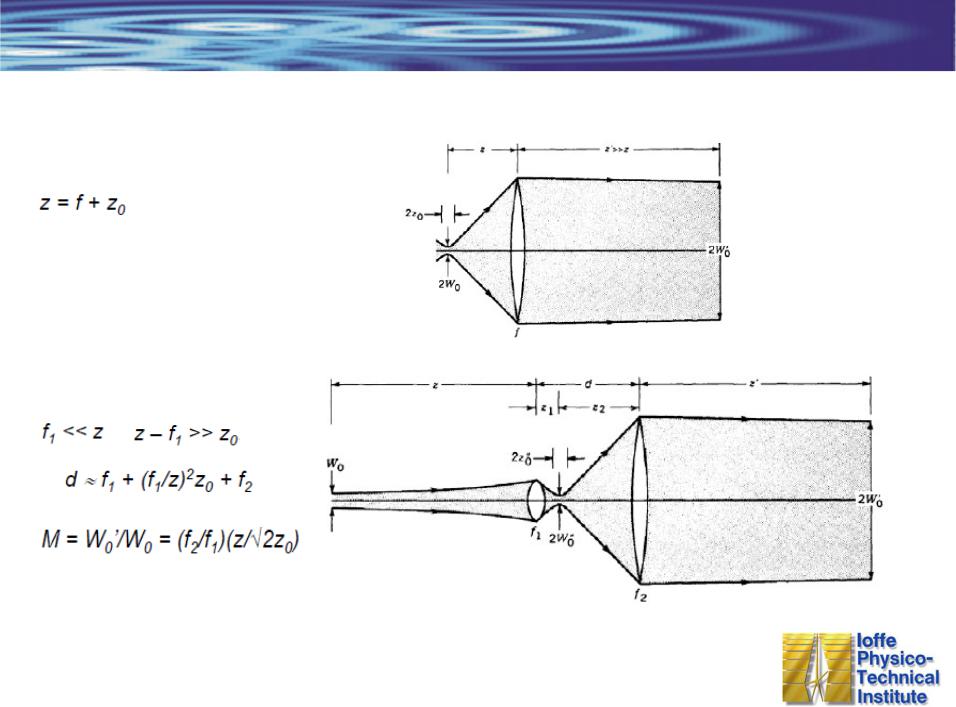
Прохождение Гауссова пучка через оптическую систему

Коллиматор

<<1

Расширение пучка

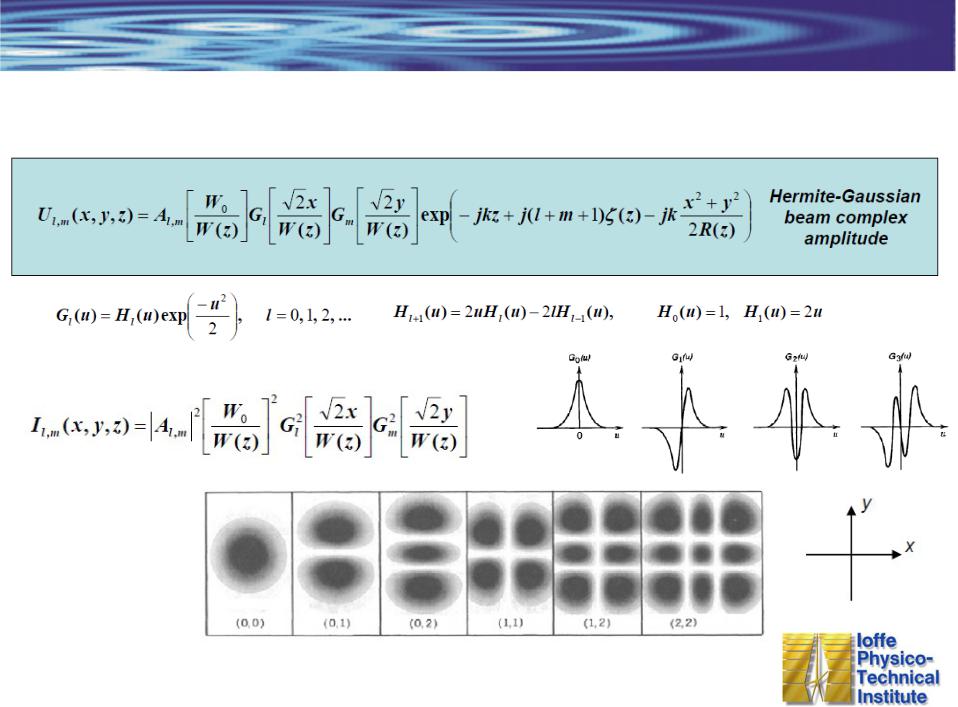
Другие решения уравнения Гельмгольца в параксиальном приближении

Все функции имеют параболический фронт с одинаковым радиусом кривизны

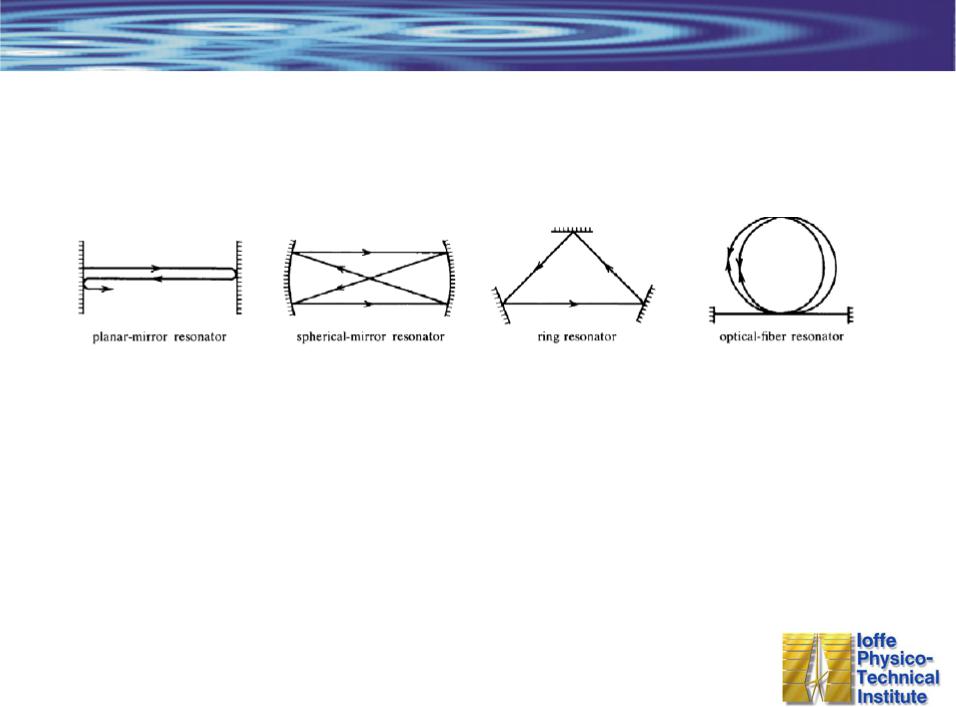
Оптические резонаторы

Накапливают энергию на определенных резонансных частотах (длинах волн)

Применение:

•Оптические фильтры

•Лазеры

Волновая оптика пучков используется для анализа мод резонаторов