
решения курсовых (семестровых) работ из задачника / Динамика / d09_07
.pdf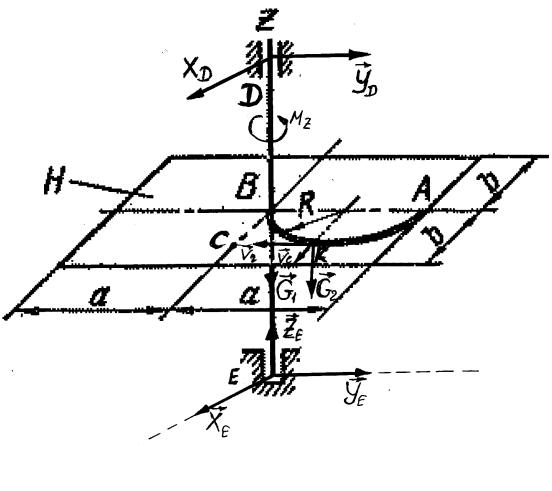
9 ( 7) http://www.termeh.ru
1 z
ω 0 ; ,
, K 2.
( t = 0 ) z = z(t).
t = τ .
ωτ H t = τ.
ωτ .
t1 = 0 (t1 – ) K ( !) !
( ) ! = s = s(t1).
ω t1 = .
, "
, ! .1.
: m1 |
= 300 , m2 = 50 , ω 0 = −2 , |
= 1.6 , b = 1 , R = 0.8 , AO = 0, |
||
M |
z |
= 968 , τ = 1 , K = s = s(t ) = 0.5π Rt2 |
, = 1 c. |
|
|
1 |
1 |
|
|
.1

http://www.termeh.ru
# $ ! !
,
dLdtz = MizE ,
Lz – , ! K ,
z; MizE = zE - $ ,
, z.
% ! t = 0 t = τ : G1 H, G2
K, z $ ( . 1).
, H
, z;
! .
% Lz , !
Jzω K,
H V = ω × BO : |
|
V ×O O = ω × O2. |
||||
|
|
|
|
2 |
1 |
2 |
!, L = J |
ω + ω × O2 |
= (J |
z |
+ × O2 )ω . |
|
|
z z |
2 |
|
|
2 |
|
|
& $ z,
z !.
', ! ,
d ((Jz + 2 × BO2 )ω) Lz = M z , (1) dt
M z = const.
( ! (1)
:
|
|
|
|
|
|
τ |
|
|
|
(Jz + 2 |
× O2 ) ωτ dω = M z dt. |
|
|||
|
|
|
|
|
ω0 |
0 |
|
|
|
|
|
|
|
|
|
(J |
z |
+ × O2 )(ω -ω |
) = M τ. |
|
(2) |
||
|
2 |
τ |
0 |
z |
|
|
|
% ! (2) . ) ( ) z ,
!*
Jz = 13 m1 (a2 + b2 ) = 13 ×300 ×(1.62 +12 ) = 356 × 2.
+! ( .1) O = = = 1.6 , = 0.
J |
z |
+ × O2 = 356 + 50 |
×1.62 |
= 484 × 2. |
|
|
|
2 |
|
|
|
|
|
!, ! (2) |
|
|
|
|
||
484 ×(ωτ - (-2)) = 968×1 |
|
ωτ = |
968 |
- 2 = 0. |
||
484 |
||||||
z H
; G1 G2,
$ ( .1).
$
t1 = 0 t1 = .

|
|
|
|
|
|
http://www.termeh.ru |
', ! , |
||||||
|
dLz |
= 0, Lz = const. |
||||
|
||||||
|
|
|
|
|
dt |
|
! Lz0 t1 = 0 Lzτ t1 = |
||||||
!. |
|
|
|
|
|
|
, t1 = 0 |
L |
= (J |
z |
+ × O2 )ω = 0. |
||
|
z 0 |
|
2 |
|
τ |
|
t1 > 0 K ! Vr
$ V .
t1 = : m2Vr 2V .
, t1 = = 1 |
|
|
L |
= J |
z |
ω + ω × K 2 |
+ V × . |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
z |
|
|
|
|
2 |
|
|
|
T |
|
2 r |
|
|
|
|
|
|
||
s |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
0.5π Rt |
|
|
|
|
πt |
|
|
|
|
|
|
π ×1 |
||||||||||||||
AKT = 2R sin |
|
|
|
|
= 2R sin |
2R |
1 |
= 2R sin |
|
1 |
= 2 ×0.8×sin |
|
4 |
= 0.8 2 . |
||||||||||||
|
|
|
|
|||||||||||||||||||||||
2R |
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|||||||||||
AKT2 = (0.8 |
|
|
)2 = 1.28 2 ; |
AB2 = a2 |
= 1.62 = 2.56 2 ; BKT2 + AKT2 |
= AB2 ; |
||||||||||||||||||||
|
2 |
|||||||||||||||||||||||||
BKT2 = AB2 - AKT2 |
= 2.56 -1.28 = 1.28 2 ; |
|
= |
|
|
= 0.8 |
|
|
» 1.131 . |
|||||||||||||||||
BKT |
1.28 |
2 |
||||||||||||||||||||||||
, AKT |
= KT , |
Vr -- AB, BC = R = 0.8 . |
||||||||||||||||||||||||
|
V |
= |
ds |
= |
d (0.5π Rt2 ) |
= |
π Rt , |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
r |
|
dt |
|
dt |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
t1 = = 1 |
|
Vr = π Rt1 = 3.14 ×0.8×1 » 2.513 . |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
Lz = 356 ×ω + 50 ×ω ×1.28 + 50 × 2.513×0.8 = 420ω +100.531 |
|||||||||||||||||||||||
|
Lz0 Lzτ : |
0 = 420ω +100.531, |
|
ω |
= -0.23936 . |
|||||||||||||||||||||
: ωτ = 0; |
ω |
= -0.23936 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
