шпоргалка / ТерМех / last

1.Условие равновесия под действием сходящейся совокупности сил. Сход. с-ть сил – силы, линии действия которых (при их продолжении) пересекаются в одной точке. Сила величина, характеризуемая: направлением, абсолютным значением и точкой приложения. Условие равновесия: чтобы тело находилось в состоянии равновесия, надо чтобы : Система: , , . Примечание: для равновесия тела под действием сходящейся совокупности сил, силы будут образовывать замкнутый силовой многоугольник.

3.Теорема Вариньона. Момент пары сил. Для сходящейся с-ти сил сумма всех моментов внешних сил равна моменту равнодействующей. Д-во: , , , . Пара сил – две антипараллельные и равные по величине силы, приложенные к разным точкам. . Выберем произвольную т. О и рассмотрим суммарный момент этих сил относительно О: . Т.е. момент пары сил будет определятся векторным произведением расстояния между точками приложения этих сил на силу. Следовательно, момент пары сил не зависит от положения полюса О. Силы ограничивающие перемещение точки – связи.

5.Сила трения качения. Параллелепипед на горизонтальной поверхности. , , h – коэффициент трения качения (определяется деформацией взаимодействия тел), Nh – момент трения качения. Рассмотрим параллелепипед на горизонтальной поверхности: . Тело будет двигаться при , , , . Относительно оси проходящей через С: , ,,. - условие вращения параллелепипеда. При условии будет качение. Движение параллелепипеда по плоскости будет определяться его геометрией и коэффициентом трения скольжения. Чистое скольжение: . Чистое качение: . Качение с проскальзыванием: .

7.Центр параллельных сил. Центр тяжести. Рассмотрим параллельные силы, приложенные к твердому телу, и сосредоточим их по направлениям. Заменяем их равнодействующей приложенной к точке С: . Лемма: если все внешние силы повернуть на один и тот же угол, то равнодйствующая повернется на тот же угол. Рассмотрим ║-ые силы, расположенные random’но. Повернем все внешние силы на одинаковый угол, чтобы они смотрели вдоль оси z: , . . По теореме Вариньона: , r_c – координаты точки приложения R. Преобразовав, учитывая, что проекции на x и y = 0, получим:. Векторы равны в случае равенства их составляющих. Отсюда: , ,,. Итак, .

9.Скорость. Ускорение. Годограф скорости и ускорения. Положение тела в пространстве описывается радиус-вектором: , . Направление определяется углами: ,,. Скорость – быстрота роста пути . Ускорение скорость изменения скорости: . Кривая, которую описывает конец радиус-вектора – годограф скорости. Кривая, которую описывает конец вектора скорости – годограф ускорения.

11. Сложение 2-х взаимно перпендикулярных колебаний одной частоты. , . Свяжем y и x исключая t, чтобы получить уравнение траектории. , . После того, как домножили, сложим: . , . , . , . . Если θ=0, то прямая слева направо под углом 45; если – π, то справа налево; если – π/2 или 3π/2, то окружность. При сложении перпендикулярных колебаний с разной частотой, устойчивые картины наблюдаются при отношении этих частот как целых чисел.

13. Натуральный триэдр скоростей и ускорений. Рассм. скалярную функцию и векторное поле , на основе этой скалярной функции.

,, ,. произв-ая вектора пост. длины самому вектору., .

Рассмотрим движение точки M по траектории и выбираем 2 момента времени, когда 2 точки по кривой достаточно близки друг к другу. - радиус кривизны, приращение кривой. Через векторы проводим плоскость (соприкасающаяся). Векторперетаскиваем из т. M₁ в т. M₂, - приращение вектора. Проводим плоскость через точку M₂, параллельно . Это плоскость называется нормальной. Откладываем вдоль прямой M₂O единичный вектор - нормальный. . Т.е в натуральном триэдре введены 2 ед. вектора . Введём ед. вектор (бинормаль) . Проекция скорости и ускорения на бинормаль всегда =0 – из-за того, что точки взяты близко друг к другу.

15. мгновенный центр скоростей. Рассм. плоское движение ТВ. Тела которое можно предситавить в виде двух независимых перемещений: 1. поступательное, 1. вращательное отн. Неподвижной точки. Выбираем произвольную точку М, которая принадлежит телу. Полное перемещение этой точки можно представить в виде 2-х перемещений - поступательно, - вращательное, отн. Т. О. , , , - направлен к нам. .МЦС – называется точка, как принадлежащая, так и не принадлежащая телу, скорость которой относительно неподвижной системы отсчёта равна нулю. , где - координаты МЦС. , , ; , , _{, .} допустим_, что известны скорость и направление скорости точки А и направление скорости точки В. Тогда МЦС будет находится на пересечении перпендикуляров проведенных к направлениям скоростей . Тогда скорость произвольной точки С будет перпендикулярна прямой СР и по абсолютной величине равна

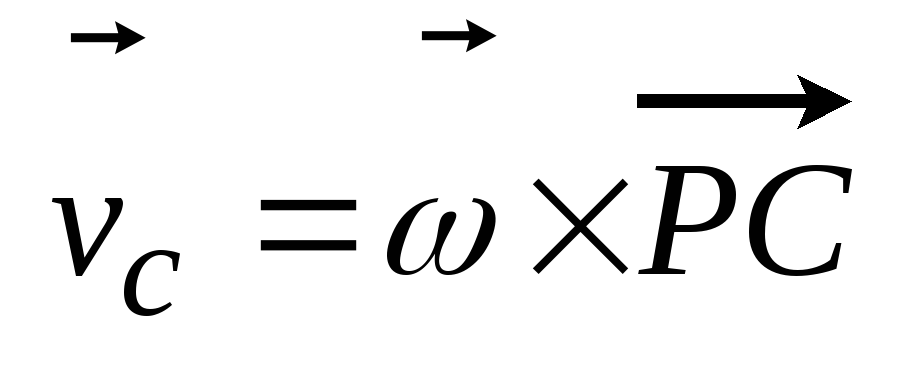
4.Сила трения скольжения. Конус трения. , , , - статистическая. , - динамическая. . Коэффициент трения зависит от материала взаимодействующих тел, степени обработки поверхности, состояния окружающей среды. Приложим к телу внешнюю силу a и направим ее под углом β к вертикали. Запишем условия равновесия: , , , , . При β≤β₀ тело не сдвинется с места при любом значении силы Q. β₀ – угол трения. Прикладывая силу в конусе с углом раствора 2β₀, тело с места не сдвинем. Этот конус – конус трения.

2. Несходящаяся с-ть сил. Момент сил. Несход. с-ть сил – силы, линии действия которых (при продолжении) не пересекаются в одной точке. Для условия равновесия не достаточно. Вводим понятие момента сил: - сумма векторных произведений. Момент сил это псевдовектор. Его направление определяется по-разному в правой и левой системах координат. В теор-мехе направление векторного произведении я определяется в левой системе координат: . Условие равновесия для несх. с-ти сил: и . Написать в проекциях.

8. Частные случаи центра тяжести. 1.Если тело симметрично относительно плоскости его пересекающей, то центр тяжести в этой плоскости. 2.Если тело симметрично относительно 2-х непараллельных плоскостей, то центр тяжести на линии их пересечения. 3.Если тело симметрично относительно трех непараллельных плоскостей, то центр тяжести в точке их пересечения. 4.Если тело общей площадью S может быть представлено в виде набора тел правильной формы с площадями S^(k) и координатами центра масс x^(k), то координаты центра масс тела можно рассчитать: . 1-я т. Папа-Гульдена: боковая п-ть плоской линии равна произведению длины этой линии на длину окружности, описываемой центром тяжести линии относительно оси вращения. 2-я т. П.-Г.: объем тела вращения плоской фигуры относительно оси, лежащей в плоскости фигуры и ее не пересекающей равен произведению площади этой фигуры на длину окружности, описываемой центром тяжести. Некоторые фигуры: ∆ - центр тяжести – точка пересечения медиан; трапеция - ; четырехугольник – делим на 2 ∆; дуга - ; сектор - .

6.Параллелепипед на наклонной плоскости. Самоторможение. Сила трения может быть направлена как вдоль оси x, так и против нее. Поэтому 2 случая. 1) , . , - угол трения. . 2) , . , . - явление самоторможения. Если выполняется это условие, то тело в покое.

12.Затухающие гармонические колебания. Зададим колебания в виде: , λ – фактор затухания, x₀ – амплитуда, a=2x₀ – размах колебаний, ω – циклическая частота, φ₀ – начальная фаза. . Найдем отношение: . , => , . Подставив в отношение, получим , - декремент колебаний. - логарифмический декремент. Взять 2-ю производную от x, чтобы получить ускорение.

10.Сложение гармонических колебаний одной частоты вдоль одной прямой. ,. , система: , . , , .

16. Поле ускорений. МЦУ. (все индексы , на самом деле Q, ошибочка вышла) , . Изменение положения от времени определяется из : , . Учитывая, что для плоского движения . . МЦУ – точка (как принадлежащая тв. телу, так и нет) ускорение которой относительно неподвижной системы отсчёта равно 0. , - координаты мгновенного центра ускорений. Умножим на слева: , _{, , ,} . предположим. Что известно ускорение и его направление в точке А. раскладываем это ускорение на осестремительную и осевращательную компоненты . Определим угол, где и под этим углом проводим прямую через т.А. на этой прямой откладываем расстояние . Т. Q – МЦУ.

14. Вращательное движение точки. , . . . - угловое ускорение. . - псевдовектор.