|
31.
Общее уравнение динамики.
Рассм. движение системы материальных
точек на которые будут действовать
внешние силы
 и внутренние силы
и внутренние силы
 .
Для системы материальных точек можно
рассм. только внешние силы, т.к. согласно
3-му з-ну Ньютона сумма всех внутренних
сил в результате даст 0. .
Для системы материальных точек можно
рассм. только внешние силы, т.к. согласно
3-му з-ну Ньютона сумма всех внутренних
сил в результате даст 0.
 - главный вектор внешних сил.
- главный вектор внешних сил.
 , ,
 - импульс и количество движения.
- импульс и количество движения.
 - главный вектор импульса. Для системы
материальных точек
- главный вектор импульса. Для системы
материальных точек
 .
Момент количества движения: .
Момент количества движения:
 , ,
 . частный случай: рассм. центральную
силу:
. частный случай: рассм. центральную
силу:
 , ,
 , ,
 , ,
 - секториальная скорость.
- секториальная скорость.
|
33.
Импульс силы.
Будем рассм. взаимодействие тел
непосредственно до удара и сразу после
удара. При этом положение системы
будет характеризоваться радиус-вектором
 ,
который, в данном случае, не изменяется ,
который, в данном случае, не изменяется
 , ,
 , ,
 , ,
 - импульс силы – является одним из
основных элементов при рассмотрении
законов сохранения импульса и момента
импульса
- импульс силы – является одним из
основных элементов при рассмотрении
законов сохранения импульса и момента
импульса

|
|
35.
Работа.
Рассм. движение тела по кривой описываем
уравнением
 .
т. M
движется по кривой под действием
внешней силы .
т. M
движется по кривой под действием
внешней силы
 .
при переходе тела массы m
из положения M1
в положение M2
будем говорить, что над телом совершается
работа равная .
при переходе тела массы m
из положения M1
в положение M2
будем говорить, что над телом совершается
работа равная
 . .
 - неполный дифференциал. Физический
смысл математически неполного
дифференциала: показывает что работа
совершаемая нал телом не всегда
определяется его конечным и начальным
положениями (для диссипативных сил
работа зависит от пути движения).
- неполный дифференциал. Физический
смысл математически неполного
дифференциала: показывает что работа
совершаемая нал телом не всегда
определяется его конечным и начальным
положениями (для диссипативных сил
работа зависит от пути движения).
|
36,
37. Кинетическая энергия системы тел.
 ,
рассм. общий случай движения. При этом
скорость ,
рассм. общий случай движения. При этом
скорость
 .
. Частный случай 1. .
. Частный случай 1.
 , ,
 , ,
 - кинетическая энергия центра масс
системы относительно неподвижного
полюса.
- кинетическая энергия центра масс
системы относительно неподвижного
полюса.
 - кинетическая энергия системы
относительно движущегося полюса O1.
- кинетическая энергия системы
относительно движущегося полюса O1.
 - кинетическая энергия системы связанная
с центром масс относительно движущегося
полюса O1.
Совмещаем центр масс с полюсом O1:
- кинетическая энергия системы связанная
с центром масс относительно движущегося
полюса O1.
Совмещаем центр масс с полюсом O1:
 , ,
 ,
т.к. ,
т.к.
 .
Частный случай 2. (кинетическая энергия
вращательного движения твёрдого тела) .
Частный случай 2. (кинетическая энергия
вращательного движения твёрдого тела)
 , ,
 .
37. Теорема
об изменении кинетической энергии. .
37. Теорема
об изменении кинетической энергии.
 , ,
 , ,
 , ,

|
|
39.
Потенциальная энергия силового поля.
Будем рассм. движение мат. точки в
произвольном силовом поле. Предположим
что точка перешла из положения 1 в
положение 2 в силовом поле. Определим
ограничения накладываемые на силовые
поля при условии что работа при переходе
из 1 в 2 не зависит от формы траектории
по которой переход совершается.
Необходимым и достаточным условием
независимости работы от траектории
перехода в силовом поле является
наличие такой потенциальной функции
для которой выполняется условие в
декартовых координатах
 .
П
– потенциальная энергия силового
поля. 1) необходимость .
П
– потенциальная энергия силового
поля. 1) необходимость
 , ,
 , ,
 .
2) достаточность. предположим, что у
нас есть такая потенциальная функция,
что для неё выполняется: .
2) достаточность. предположим, что у
нас есть такая потенциальная функция,
что для неё выполняется:
 .
Пусть для определённости .
Пусть для определённости
 .
Предположим, что лдя малого перемещения
из 1 в 2, работа .
Предположим, что лдя малого перемещения
из 1 в 2, работа
 , ,
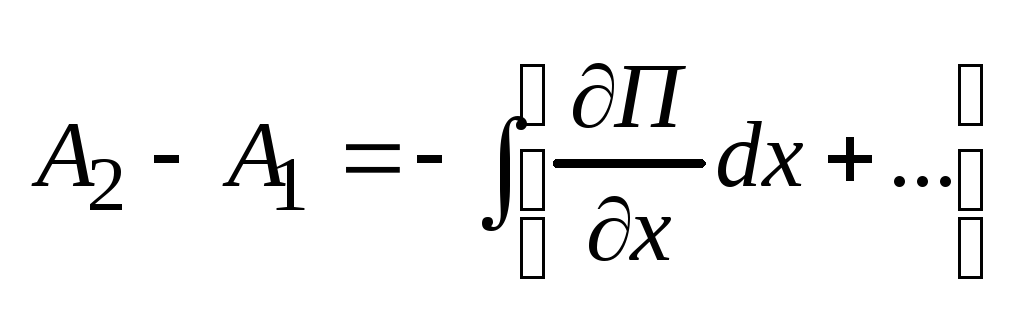
|
4 1.
Виртуальные перемещения жёсткого
стержня.
Рассмотрим движение системы тел,
ограниченное связями. Перемещение
этих тел можно представить в виде
суммы двух перемещений: 1) перемещение
при условии, что связи в этот момент
зафиксированы и не меняются 2) перемещение
за счёт изменения самих связей. Первый
тип перемещений носит название
виртуальных. Допустим перемещение
описывается функцией 1.
Виртуальные перемещения жёсткого
стержня.
Рассмотрим движение системы тел,
ограниченное связями. Перемещение
этих тел можно представить в виде
суммы двух перемещений: 1) перемещение
при условии, что связи в этот момент
зафиксированы и не меняются 2) перемещение
за счёт изменения самих связей. Первый
тип перемещений носит название
виртуальных. Допустим перемещение
описывается функцией
 .
Действит. перемещения .
Действит. перемещения
 , ,
 - виртуальное перемещение. Если
координаты выразить через обобщённые
координаты,
- виртуальное перемещение. Если
координаты выразить через обобщённые
координаты,
 то
виртуальные координаты можно выразить то
виртуальные координаты можно выразить
 Виртуальные перемещения жёсткого
стержня.
Виртуальные перемещения жёсткого
стержня.
 , ,
 , ,
 , ,
  .
Т.е проекция виртуальных перемещений
на направление длины стержня должны
совпадать. .
Т.е проекция виртуальных перемещений
на направление длины стержня должны
совпадать.
|
|
43.
Принцип виртуальных перемещений.
Даёт возможность анализировать при
каких условиях тело, либо система тел
подверженная внешним силам и связям
будет находится в равновесии. Для того
чтобы система тел ограниченная
идеальными связями находилась в
равновесии необходимо и достаточным
условием является равенство 0 для
элементарных работ внешних сил на
виртуальны перемещениях
 1) необходимость
1) необходимость
 , ,
 .
2) достаточность. Предположим, что .
2) достаточность. Предположим, что
 , ,
 , ,
 , ,
 .
Для консервативных сил: .
Для консервативных сил:
 , ,
 , ,
 . .
 , ,
 . .
|
45.
Применение принципа виртуальных
перемещений.
Рассмотрим в декартовой системе
координат:
 .
В общем случае система может совершать
как поступательное .
В общем случае система может совершать
как поступательное
 так и вращательное перемещение
так и вращательное перемещение
 . .
 . .
 , ,
 .
Такая записаь допустима в силу линейной
независимости векторов .
Такая записаь допустима в силу линейной
независимости векторов
 друг от друга. Эти условия являются
условиями равновесия для нисходящей
совокупности сил.
друг от друга. Эти условия являются
условиями равновесия для нисходящей
совокупности сил.
|
|
34.
момент импульса в движущейся системе
отсчёта.
Полюс O1
относительно неподвижной системы
движется со скоростью
 и сама система движется скоростью
и сама система движется скоростью
 : :
 : :
 . .
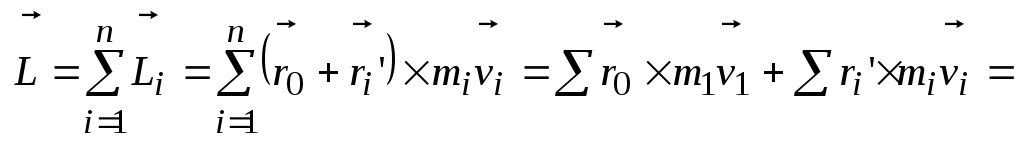 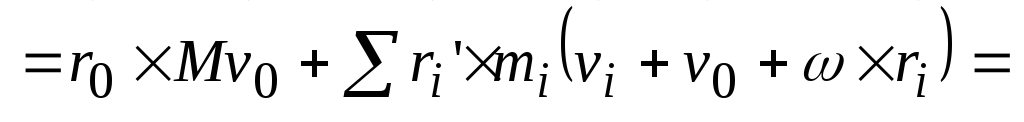  . .
 - момент импульса системы движущейся
со скоростью
- момент импульса системы движущейся
со скоростью
 . .
 момент импульса всей системы относительно
полюса O1
(в случае если центр масс совпадает с
полюсом O1,
момент импульса будет равен 0, поскольку
положение центра масс описывается
нулевым вектором по отношению к O1).
момент импульса всей системы относительно
полюса O1
(в случае если центр масс совпадает с
полюсом O1,
момент импульса будет равен 0, поскольку
положение центра масс описывается
нулевым вектором по отношению к O1).
 - момент испульса центра масс относительно
неподвижной точки O.
- момент испульса центра масс относительно
неподвижной точки O.
|
32.
Центр масс. Скорость центра масс. Т-ма
Эйлера.
Рассм. системы материальных точек mi,
находящихся относительно полюса на
расст.
 эту систему можно заменить обще массой
эту систему можно заменить обще массой
 в
положении в
положении
 ,
скорость ,
скорость
 .
Т-ма Эйлера:
рассм. жидкость протекающую через
выделенный объём. Весь объём разобьем
на трубки тока, в пределах которых
скорость жидкости можно считать
постоянной. Силы действующие на
жидкость внутри трубки разобъём на 2
класса: 1) объёмные силы .
Т-ма Эйлера:
рассм. жидкость протекающую через
выделенный объём. Весь объём разобьем
на трубки тока, в пределах которых
скорость жидкости можно считать
постоянной. Силы действующие на
жидкость внутри трубки разобъём на 2
класса: 1) объёмные силы
 ,
т.е. силы, которые будут действовать
на все элементы жидкости внутри
выделенного объёма, 2) поверхностные
силы ,
т.е. силы, которые будут действовать
на все элементы жидкости внутри
выделенного объёма, 2) поверхностные
силы
 .
.
 , ,
 , ,
 , ,
 . .
 , ,
 . .
 - теорема Эйлера.
- теорема Эйлера.
|
|
38.
Поступательно-вращательное движение
твёрдого тела.
Такое движение можно представить в
виде двух независимых перемещений.
При этом кинетической энергии в общем
виде может быть представлена как сумма
двух энергий: поступательная
 и вращательная
и вращательная
 .
Общая энергия .
Общая энергия
 . .
 - радиус инерции, его физический смысл
заключается в том, что твёрдое тело
заменяется точкой массы M
находящейся на расстоянии ρ от оси
вращения
- радиус инерции, его физический смысл
заключается в том, что твёрдое тело
заменяется точкой массы M
находящейся на расстоянии ρ от оси
вращения
 , ,
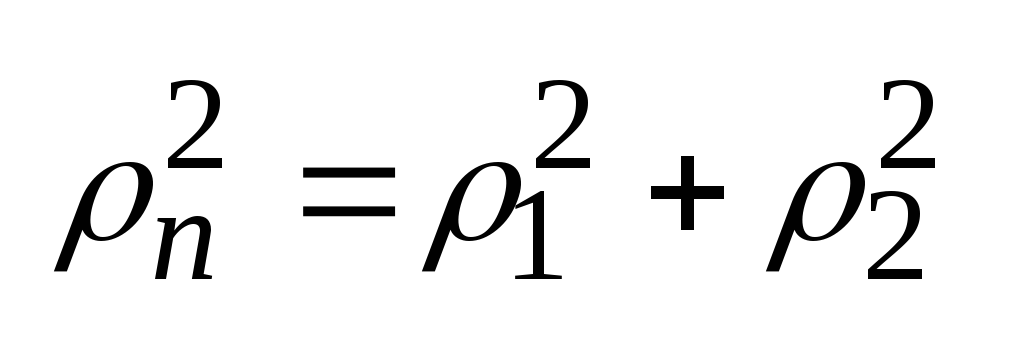
|
36,
37. Кинетическая энергия системы тел.
 ,
рассм. общий случай движения. При этом
скорость ,
рассм. общий случай движения. При этом
скорость
 .
. Частный случай 1. .
. Частный случай 1.
 , ,
 , ,
 - кинетическая энергия центра масс
системы относительно неподвижного
полюса.
- кинетическая энергия центра масс
системы относительно неподвижного
полюса.
 - кинетическая энергия системы
относительно движущегося полюса O1.
- кинетическая энергия системы
относительно движущегося полюса O1.
 - кинетическая энергия системы связанная
с центром масс относительно движущегося
полюса O1.
Совмещаем центр масс с полюсом O1:
- кинетическая энергия системы связанная
с центром масс относительно движущегося
полюса O1.
Совмещаем центр масс с полюсом O1:
 , ,
 ,
т.к. ,
т.к.
 .
Частный случай 2. (кинетическая энергия
вращательного движения твёрдого тела) .
Частный случай 2. (кинетическая энергия
вращательного движения твёрдого тела)
 , ,
 .
37. Теорема
об изменении кинетической энергии. .
37. Теорема
об изменении кинетической энергии.
 , ,
 , ,
 , ,

|
|
42.
Идеальные связи.
Под идеальными связями будем понимать
такие связи, сумма от элементарных
работ для которых на виртуальных
перемещениях равна нулю .
 .
Другие связи с точки зрения динамики
как внешние ограничения силы .
Другие связи с точки зрения динамики
как внешние ограничения силы
 - работа.
- работа.


  , ,
 - обобщённая сила.
- обобщённая сила.
|
40.
Плоско-вращательное движение твёрдого
тела.
 ,
рассм. качение цилиндра по наклонной
плоскости: ,
рассм. качение цилиндра по наклонной
плоскости:
 .
Для того, чтобы замкнуть систему
сравнений рассмотрим кинематическую
связь между углом поворота .
Для того, чтобы замкнуть систему
сравнений рассмотрим кинематическую
связь между углом поворота
 : :
 , ,
 , ,
 , ,
 , ,
 , ,
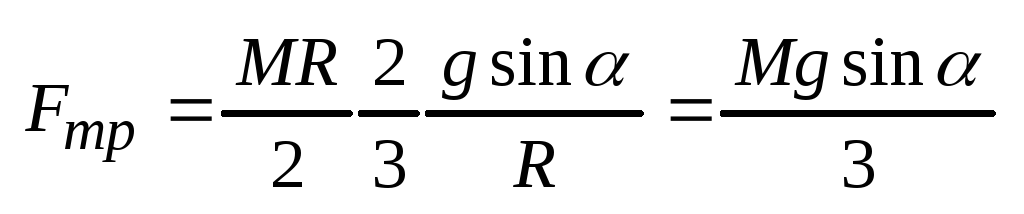
|
|
46.
Принцип Даламбера.
Ур-ие Ньютона:
 ; ; - ускорения которые имели бы место в
случае отсутствия связей
- ускорения которые имели бы место в
случае отсутствия связей
 - потерянные ускорения.
- потерянные ускорения.
 - сила инерции.
- сила инерции.
 - потерянные силы.
- потерянные силы.
 принцип Даламбера. Формально принцип
Даламбера переводит задачу динамики
движения несвободной системы в задачу
статики
принцип Даламбера. Формально принцип
Даламбера переводит задачу динамики
движения несвободной системы в задачу
статики
|
44.
Общий принцип виртуальных перемещений
для несвободных систем.
Рассм. обобщённые силы
 .
Пусть на систему действуют кинематические
связи .
Пусть на систему действуют кинематические
связи
 .
Если все обобщённые координаты линейно
независимы друг от друга то общий
принцип виртуальных перемещений можно
записать: .
Если все обобщённые координаты линейно
независимы друг от друга то общий
принцип виртуальных перемещений можно
записать:
 .
В силу независимости обобщённых
координат это справедливо в случае .
В силу независимости обобщённых
координат это справедливо в случае
 .
Если не все обобщённые координаты
являются линейнонезависимыми и
ограничиваются кинематическими
связями, то тогда общий принцип
виртуальных перемещений: .
Если не все обобщённые координаты
являются линейнонезависимыми и
ограничиваются кинематическими
связями, то тогда общий принцип
виртуальных перемещений:
 , ,
 - множитель связи, который переводит
размерность кинематической связи в
размерность силы.
- множитель связи, который переводит
размерность кинематической связи в
размерность силы.
|


 .
.
 1.
Виртуальные перемещения жёсткого
стержня.
Рассмотрим движение системы тел,
ограниченное связями. Перемещение
этих тел можно представить в виде
суммы двух перемещений: 1) перемещение
при условии, что связи в этот момент
зафиксированы и не меняются 2) перемещение
за счёт изменения самих связей. Первый
тип перемещений носит название
виртуальных. Допустим перемещение
описывается функцией
1.
Виртуальные перемещения жёсткого
стержня.
Рассмотрим движение системы тел,
ограниченное связями. Перемещение
этих тел можно представить в виде
суммы двух перемещений: 1) перемещение
при условии, что связи в этот момент
зафиксированы и не меняются 2) перемещение
за счёт изменения самих связей. Первый
тип перемещений носит название
виртуальных. Допустим перемещение
описывается функцией
 .
.
 .
Т-ма Эйлера:
рассм. жидкость протекающую через
выделенный объём. Весь объём разобьем
на трубки тока, в пределах которых
скорость жидкости можно считать
постоянной. Силы действующие на
жидкость внутри трубки разобъём на 2
класса: 1) объёмные силы
.
Т-ма Эйлера:
рассм. жидкость протекающую через
выделенный объём. Весь объём разобьем
на трубки тока, в пределах которых
скорость жидкости можно считать
постоянной. Силы действующие на
жидкость внутри трубки разобъём на 2
класса: 1) объёмные силы
 ,
,