|
17.Криволинейная
СК.
 .
Квадрат дифференциала дуги - .
Квадрат дифференциала дуги -
 .ДСК: .ДСК:
 .
Цилиндрическая: .
Цилиндрическая:
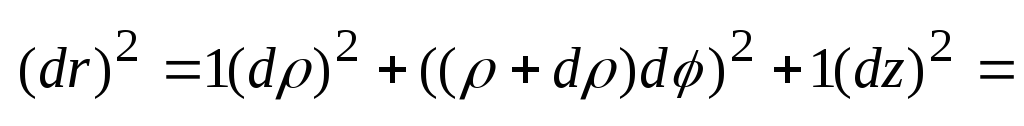 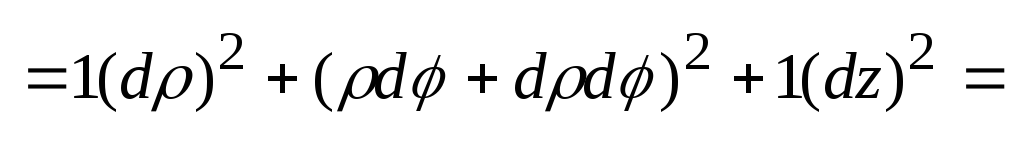  .
Сферическая: .
Сферическая:
 . . =>Коэффициенты
Ламе: ДСК - =>Коэффициенты
Ламе: ДСК -
 ;
цилиндрическая - ;
цилиндрическая -
 ;
сферическая - ;
сферическая -
 . .
|
19.
Движение тела по эллипсу.
Будем рассм. движение спутника
относительно более массивного тлеа,
помещённого в один их полюсов эллипса.
Будем рассм. движение на основе трёх
законов Кеплера. Й-ый з-н:
 , ,
 ,. ,.
 ;
2-ой з-н: при движении по эллипсы
секториальная скорость является
величиной постоянной. ;
2-ой з-н: при движении по эллипсы
секториальная скорость является
величиной постоянной.
 - секториальная скорость,
- секториальная скорость,
 , ,
 , ,
 .
3-ий з-н: .
3-ий з-н:
 , ,
 , ,
 , ,
 , ,
 . .
|
|
21.
Скорость точки в неподвижной системе
координат.
 - абсолютная,
- абсолютная,
 - относительная,
- относительная,
 - переносная скорость.
- переносная скорость.
 , ,
 , ,
 .
Поскольку для .
Поскольку для
 как координаты
как координаты
 так и орты могут изменяться во времени,
то производная
так и орты могут изменяться во времени,
то производная
 ; ;
 , ,
 , ,
 . .
 . .
|
23.
Классификация сил.
Два класса: 1. силы ограничивающие
перемещение системы (связи). 2. внешние
чилы, которые вызывают движение
системы. Классификация:
1. постоянные по величине и направлению
(сила Лоренца, например). 2.
позиционные силы – зависящие от
положения тел в пространстве
(гравитационные, электромагнитные,
ядерные, слабые). 3. стационарные силы
(нестационарные), (пример: магнитная
сила). 4. силы, зависящие от скорости
(все диссипативные силы вязкости,
сопр. воздуха). 5. силы зависящие от
ускорения.
|
|
25.
движение в поле центральных сил.
Центральные силы – силы, линия действия
которых всегда проходит через одну и
ту же точку.
 , ,
 , ,
 .
Ур-ие движения в полярных координатах .
Ур-ие движения в полярных координатах
 (2),
(2),

 -секторная
скорость (2-ой з-н Кеплера). -секторная
скорость (2-ой з-н Кеплера).
 .
Освободимся от времени: .
Освободимся от времени:
 : :
 , ,
 (4).
(4).
 (5). Два последних в (2):
(5). Два последних в (2):
 , ,
 , ,
 (6).
2-ая космическая скорость (6).
2-ая космическая скорость
 .
(6) можно переписать: .
(6) можно переписать:
 (6') – ур-ие Бене. Решая его
(6') – ур-ие Бене. Решая его
 , ,
 ,
где ,
где
 , ,
 - угол истинной аномалии
- угол истинной аномалии ,
1) эллипс ,
1) эллипс
 ,
2) парабола ,
2) парабола
 ,
3) гипербола ,
3) гипербола
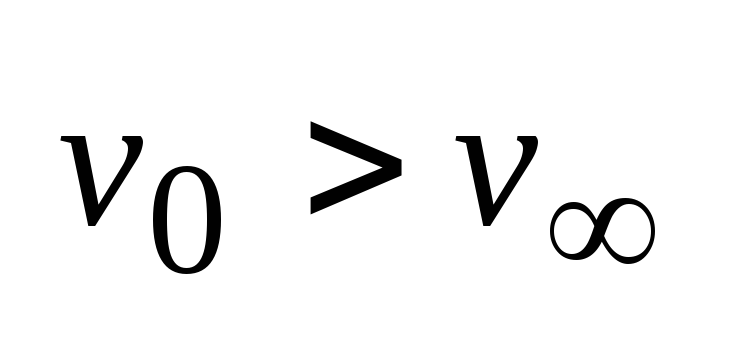
|
28. Гармонические
колебания при наличии вынуждающей
силы.
 ,
t=0,
x=x0, ,
t=0,
x=x0,
 , ,
 , ,
 , ,
 - квадрат собственной частоты.
- квадрат собственной частоты.
 , ,
 , , , ,
 .
При наличии вынуждающей силы: рассм.
системы на которую будут действовать
две силы возвращающая и вынуждающая .
При наличии вынуждающей силы: рассм.
системы на которую будут действовать
две силы возвращающая и вынуждающая
 , ,
 - амплитуда вынуждающей силы, p
– её частота.
- амплитуда вынуждающей силы, p
– её частота.
 , ,
 . .
 , ,
 . .
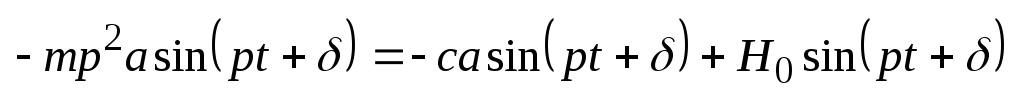  . .
 , ,
 , ,
 , ,
 . .
 , ,
|
|
27.
восходящее движение.
Под диссипативными средами будем
понимать среды в которых силы
сопротивления пропорциональны скорости
(при малых скоростях), квадрату скорости
(при больших скоростях). Рассм. движение
тела по вертикали под действием 2-х
сил: силы тяжести и силы сопротивления
пропорциональной квадрату скорости
 .
Восходящее движение: .
Восходящее движение:
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 . .
 ,
если ,
если
 , ,
 , ,
 .
Определим .
Определим
 : :
 , ,
 , ,
|
29.
Гармонические колебания при наличии
возвращающих диссипативных сил.
 ,
t=0,
x=x0, ,
t=0,
x=x0,
 , ,
 , ,
 , ,
 - квадрат собственной частоты.
- квадрат собственной частоты.
 , ,
 , , , ,
 .
Будем считать что диссипативная силы
пропорциональна скорости .
Будем считать что диссипативная силы
пропорциональна скорости
 , ,
 , ,
 : :
 , , , ,
 . .
 - фактор затухания.
- фактор затухания.
 , ,
 - общее решение,
- общее решение,
 , ,
 . .
 .
Частные случаи: а) .
Частные случаи: а)
 - апериодические затухающие колебания
б)
- апериодические затухающие колебания
б)
 -
(колебания частоты меньше собственной
частоты) – затухающие колебания в
слабодиссипативных средах. Уменьшение
амплитуды колебаний определяется
фактором затухания. в) -
(колебания частоты меньше собственной
частоты) – затухающие колебания в
слабодиссипативных средах. Уменьшение
амплитуды колебаний определяется
фактором затухания. в)
 - движение в очень вязких средах.
Колебания в данном члучает отсутствуют
и тело выведенное из положения
равновесия либо медленно вернётся в
него, либо может и не дойти.
- движение в очень вязких средах.
Колебания в данном члучает отсутствуют
и тело выведенное из положения
равновесия либо медленно вернётся в
него, либо может и не дойти.
|
|
2 0.
Абсолютное, относительное и переносное
движение.
Будем рассм. движение тела относительно
двух систем отсчёта. Первая система
неподвижна, вторая движется по заданному
закону относительно неподвижной.
Будем рассм. тело, движущееся произвольным
образом по отношению к этим двум
системам. Движение тела по отношению
к неподвижной системе отсчёта
называется абсолютным 0.
Абсолютное, относительное и переносное
движение.
Будем рассм. движение тела относительно
двух систем отсчёта. Первая система
неподвижна, вторая движется по заданному
закону относительно неподвижной.
Будем рассм. тело, движущееся произвольным
образом по отношению к этим двум
системам. Движение тела по отношению
к неподвижной системе отсчёта
называется абсолютным
 .
Движение тела, относительно движущейся
системы отсчёта будет относительным .
Движение тела, относительно движущейся
системы отсчёта будет относительным
 .
Под переносным движением понимают
движение той точки (отн. неподв.
системы), через который в данный момент
проходит тело .
Под переносным движением понимают
движение той точки (отн. неподв.
системы), через который в данный момент
проходит тело
 . .
 , ,
 , ,
 , ,


 , ,
 , ,
 - ускорение Кориолиса. Эти ускорения
приведены в правой ситсеме координат.
Для левой системы
- ускорение Кориолиса. Эти ускорения
приведены в правой ситсеме координат.
Для левой системы
 . .
|
18.Проекции
ускорений. ДСК:
 , ,
 , ,
 , ,
 , ,
 , ,
 .
Цилиндрическая: .
Цилиндрическая:
 , ,
 , ,
 , ,
 , ,
 , ,
 .
Сферическая: .
Сферическая:
 , ,
 , ,
 , ,
 , ,
 , ,
 . .
|
|
1-ая
задача динамики:
зная координаты движения тела
 , ,
 , ,
 ,
восстановить те силы, которые определяют
траекторию движения ,
восстановить те силы, которые определяют
траекторию движения
 .
Решается с помощью .
Решается с помощью
 и сводится к вычислению вторых
производных по времени от заданных
функций. 2-ая
задача:
зная действующие на систему силы F,
определить траекторию движения
системы, кинематические х-ки
и сводится к вычислению вторых
производных по времени от заданных
функций. 2-ая
задача:
зная действующие на систему силы F,
определить траекторию движения
системы, кинематические х-ки
 , ,
 , ,
 .
Сила может зависеть от времени,
положения точки пр-ве и от скорости
её движения. Дифф. ур-ия: .
Сила может зависеть от времени,
положения точки пр-ве и от скорости
её движения. Дифф. ур-ия:
 .
Нахождение з-на движения сводится к
интегрированию этой системы.
Проинтегрировав получим .
Нахождение з-на движения сводится к
интегрированию этой системы.
Проинтегрировав получим
 ,
где с – произвольные постоянные, т.е.
под действием данной силы тело совершает
не какое-то опр. движение, а может
совершать целый класс движений,
определяемый этими константами. Для
того чтобы конкретизировать задачу
необходимо ввести нач. условия, т.е.
для ,
где с – произвольные постоянные, т.е.
под действием данной силы тело совершает
не какое-то опр. движение, а может
совершать целый класс движений,
определяемый этими константами. Для
того чтобы конкретизировать задачу
необходимо ввести нач. условия, т.е.
для
 задать нач. положение и нач. скорость
задать нач. положение и нач. скорость
 .
По ним определяются постоянные
интегрирования. Для этого взяв
производные по времени от найденных
ур-ий, находят проекции скорости .
По ним определяются постоянные
интегрирования. Для этого взяв
производные по времени от найденных
ур-ий, находят проекции скорости
 .
Подставив нач. данные получим 6
алгебраических ур-ий. Решая которую
найдем значение постоянных интегрирования. .
Подставив нач. данные получим 6
алгебраических ур-ий. Решая которую
найдем значение постоянных интегрирования.
|
22.
Ускорение точки в неподвижной системе
координат.
 , ,
 , ,
 , ,
 - здесь
- здесь
 - учитывает поворот ортов на угол φ.
- учитывает поворот ортов на угол φ.

 ,
где ,
где
 - угловое ускорение.
- угловое ускорение.
 , ,
 , ,
 - специфическое (кориолисово) ускорение.
- специфическое (кориолисово) ускорение.
 .
Направление .
Направление
 - независит от вида СК (левая или правая)
- независит от вида СК (левая или правая)
|
|
28.
Гармонические колебания при наличии
вынуждающей силы. (ПРОДОЛЖЕНИЕ)
 , ,
 - гармонические колебания собственной
частоты,
- гармонические колебания собственной
частоты,
 - колебания собственной частоты под
действием вынуждающей силы.
- колебания собственной частоты под
действием вынуждающей силы.
 колебания с частотой вынуждающей
силы. Частный случай – резонанс, когда
колебания с частотой вынуждающей
силы. Частный случай – резонанс, когда

|
26.
нисходящее движение.
Под диссипативными средами будем
понимать среды в которых силы
сопротивления пропорциональны скорости
(при малых скоростях), квадрату скорости
(при больших скоростях). Рассм. движение
тела по вертикали под действием 2-х
сил: силы тяжести и силы сопротивления
пропорциональной квадрату скорости
 .
Нисходящее движение: .
Нисходящее движение:
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 .
Два случая: .
Два случая:
 . .
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,
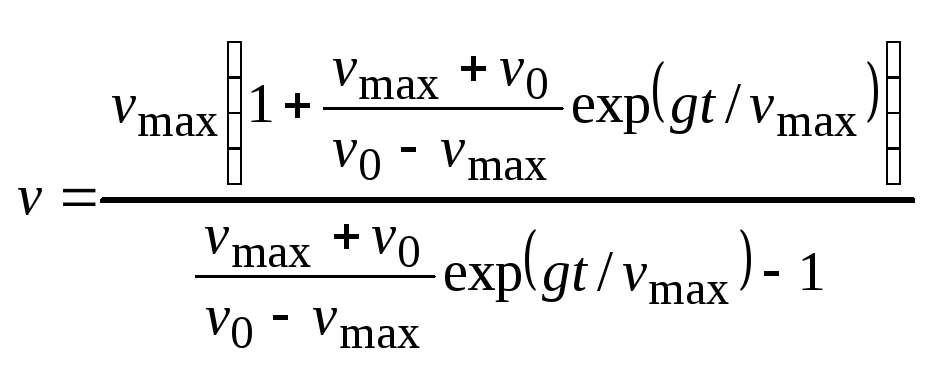
|
|
30.
движение тела переменной массы.
Под таким движением подразумевается
движение ракет, капель, образующих
облака, капель дождя, движение метеоритов
в воздухе.
Рассм.
промежуток времени dt
в течении которого масса dm
выбрасывается со скоростью c
относительно массы M
получающей приращение скорости dv.
 , ,
 , ,
 изменение импульса:
изменение импульса:
 , ,
 , ,
 , ,
 . .
|
27.
восходящее движение. (продолжение)
 , ,
 , ,
 . .
 . .
 , ,
 , ,
 , ,
 , ,
 , ,
 , ,

|


 .
Квадрат дифференциала дуги -
.
Квадрат дифференциала дуги -

 .
.
 ,
,
 ,
,
 ,
,
 .
.
 ,
,
 0.
Абсолютное, относительное и переносное
движение.
Будем рассм. движение тела относительно
двух систем отсчёта. Первая система
неподвижна, вторая движется по заданному
закону относительно неподвижной.
Будем рассм. тело, движущееся произвольным
образом по отношению к этим двум
системам. Движение тела по отношению
к неподвижной системе отсчёта
называется абсолютным
0.
Абсолютное, относительное и переносное
движение.
Будем рассм. движение тела относительно
двух систем отсчёта. Первая система
неподвижна, вторая движется по заданному
закону относительно неподвижной.
Будем рассм. тело, движущееся произвольным
образом по отношению к этим двум
системам. Движение тела по отношению
к неподвижной системе отсчёта
называется абсолютным
 ,
,
 - колебания собственной частоты под
действием вынуждающей силы.
- колебания собственной частоты под
действием вынуждающей силы.
 колебания с частотой вынуждающей
силы. Частный случай – резонанс, когда
колебания с частотой вынуждающей
силы. Частный случай – резонанс, когда
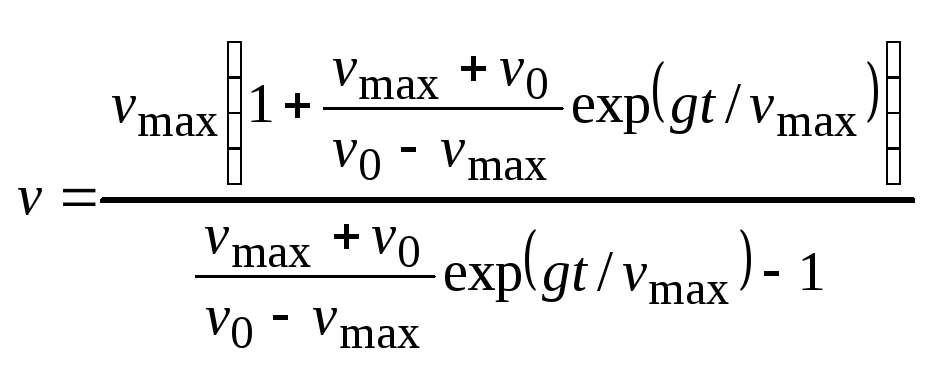

 ,
,
 .
.
 ,
,
 ,
,
 ,
,