шпоргалка / ТерМех / 13. Натуральный триэдр скоростей и ускорений

13. Натуральный триэдр скоростей и ускорений. Рассм. скалярную функцию и векторное поле , на основе этой скалярной функции. , , , 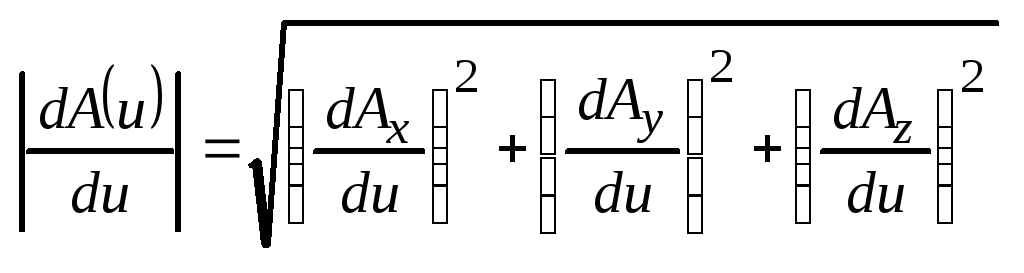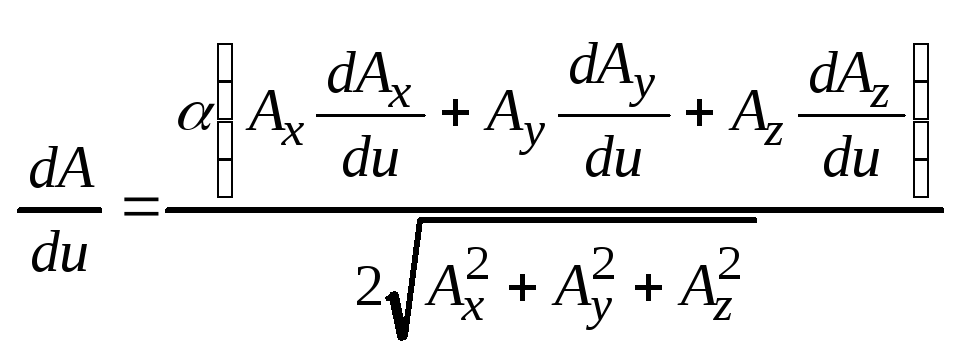. Докажем что производная вектора постоянной длины самому вектору.

. Рассмотрим движение точки M по траектории и выбираем 2 момента времени, когда 2 точки по кривой достаточно близки друг к другу. - радиус кривизны, приращение кривой. Через векторы проводим плоскость (соприкасающаяся). Векторперетаскиваем из т. M₁ в т. M₂, - приращение вектора. Проводим плоскость через точку M₂, параллельно . Это плоскость называется нормальной. Откладываем вдоль прямой M₂O единичный вектор - нормальный. . Т.е в натуральном триэдре введены 2 ед. вектора . Введём ед. вектор (бинормаль) . Проекция скорости и ускорения на бинормаль всегда =0 – из-за того, что точки взяты близко друг к другу.