шпоргалка / Динамика / 3-5 билет

3. Дифференциальные уравнения прямолинейного движения точки.

Движение материальной точки будет прямолинейным, когда действующая на нее сила (или равнодействующая приложенных сил) имеет постоянное направление, а скорость точки в начальный момент времени равна нулю или направлена вдоль силы.

Если при прямолинейном движении направить вдоль траектории координатную ось Ох, то движение точки будет определяться уравнением

m d²x/dt² = ∑F_kx или

Уравнение называют дифференциальным уравнением прямоли­нейного движения точки. Иногда его удобнее заменить двумя урав­нениями, содержащими первые производные:

m dυ_x/dt = ∑F_kx , d²x/dt² = υ_x .

В случаях, когда при решении задачи надо искать зависимость скорости от координаты x, а не от времени t (или когда сами силы зависят от х), уравнение преобразуют к переменному х. Так как dυ_x/dt = dυ_x/dx ∙ dx/dt = dυ_x/dx ∙ υ_x , то вместо получим:

mυ_x dυ_x/dt = ∑F_kx , dx/dt = υ_x .

В случае прямолинейного движения начальные условия задаются в виде

при t = 0 x = x₀, υ_x = υ₀.

По начальным условиям можно определить конкретные значения постоянных C₁ и C₂ и найти частное решение уравнения (m d²x/dt² = ∑F_kx или ), дающее закон движения точки, в виде

x = f(t, x₀, υ₀) .

4. Количество движения точки. Импульс силы.

Одной из основных динамических характеристик движения точки является количество движения.

Количество движения материальной точки - вектор­ная величина mυ, равная произведению массы точки на ее скорость.

Направлен вектор mυ так же, как и скорость точки, т. е. по ка­сательной к ее траектории.

Единицей измерения количества движения является в СИ - 1 кг∙м/с = 1 Н∙с, а в системе МКГСС-1 кГ∙с.

Импульс силы. Для характеристики действия, оказывае­мого на тело силой за некоторый промежуток времени, вводится понятие об импульсе силы. Сначала введем понятие об элементарном импульсе, т. е. об импульсе за элементарный промежуток времени dt. Элементарный импульс силы - векторная величина dS, равная произведению силы F на элементарный промежуток времени dt:

dS = Fdt.

Направлен элементарный импульс вдоль линии действия силы.

Импульс S любой силы F за конечный промежуток времени t₁ вычисляется как предел интегральной суммы соответствующих элементарных импульсов, т. е.

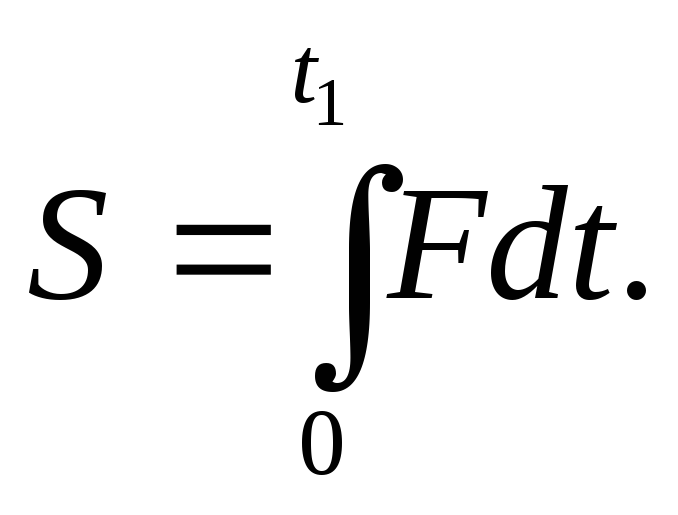
Следовательно, импульс силы за некоторый промежуток времени t₁ равен определенному интегралу от элементарного импульса, взятому в пределах от нуля до t₁ .

В частном случае, если сила F постоянна и по модулю, и по на­правлению (F = const), то S = Ft₁. Причем в этом случае и модуль S = Ft₁. В общем случае модуль импульса может быть вычислен по его проекциям на координатные оси:

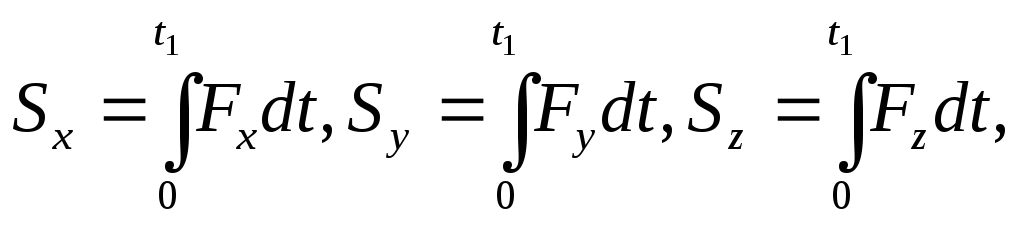
Единицей измерения импульса силы, как и количества движения, является в СИ — 1 кг ∙ м/с, а в системе МКГСС — 1 кГ ∙ с.

5. Теорема об изменении количества движения точки.

Так как масса точки постоянна, а ее ускорение a = dυ/dt, то уравнение (ma = ∑F_k), выражающее основной закон динамики, можно представить в виде

d (mυ)/dt = ∑F_k .

Уравнение выражает одновременно теорему об изменении количества движения точки в дифференциальной форме: производная по времени от количества движения точки равна сумме действующих на точку сил.

Пусть движущаяся точка имеет в момент времени t = 0 скорость υ₀, а в момент t₁ - скорость υ₁. Умножим тогда обе части равенства на dt и возьмем от них определенные интегралы. При этом спра­ва, где интегрирование идет по времени, пределами интеграла будут 0 и t₁, а слева, где интегрируется скорость, пределами интеграла будут соответствующие значения скорости υ₀ и υ₁ Так как интеграл от d(mυ) равен mυ, то в результате получим

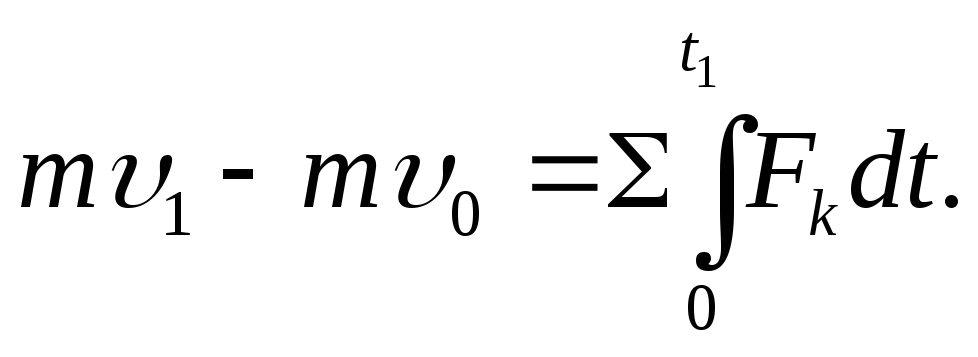
Стоящие справа интегралы, как следует из формулы, представляют собой импульсы действующих сил. Поэтому окончательно будет

Уравнение выражает теорему об изменении количества движения точки в конечном виде: изменение количества движения точки за некоторый промежуток времени равно сумме импульсов всех действующих на точку сил за тот же промежуток времени.

При решении задач вместо векторного уравнения часто поль­зуются уравнениями в проекциях. Проектируя обе части равенства на координатные оси, получим

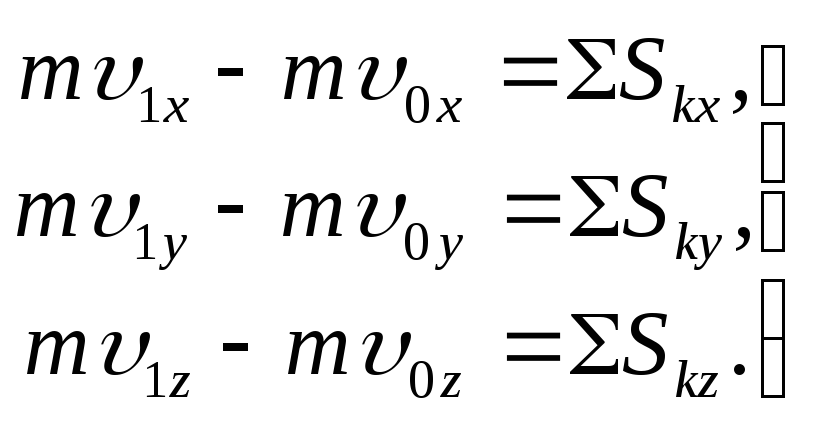
В случае прямолинейного движения, происходящего вдоль оси Ох, теорема выражается первым из этих уравнений.