шпоргалка / Тер-мех

8) Векторный, координатный и естественный способы заданий движения точки.

1 )Векторный способ, состоит в задании радиус вектора проведённого из начала координат системы отсчёта к движущейся точке как функция от времени.

2 ) Координатный способ считается заданным, если известны координаты заданной точки как функция от времени.

3)Естественный способ состоит в задании:

а) начала отсчёта

б) траектории точки

в ) направление движения точки

9)Поступательное движение, вращение вокруг неподвижной оси. Плоское движение твёрдых тел.

1)Поступательное движение тела – такое движение тела, при котором прямая соединяющая любые две его точки перемещается параллельно самой себе.

К оординаты центра тяжести

к ак функция от времени:

2)Вращательное движение тела – такое движение тела, при ко тором в любой момент времени существуют две неподвижные точки неизменно связанные с этим телом (эти точки не обязательно принадлежат этому телу).

Уравнение движения тела, есть угол  как функция от времени =(t).

Мгновенная угловая скорость:

У гловое ускорение:

Ось вращения –это прямая соединяющая две неподвижные точки вокруг которых происходит вращение, все точки лежащие на оси вращения не подвижны все точки твёрдого тела при его вращении перемещаются по круговым орбитам в плоскости, которая перпендикулярна оси вращения радиусы этих окружностей равны расстояниям соответствующих точек от оси вращения.

3 )Плоское движение твёрдого тела – такое движение, при котором все точки данного тела движутся в плоскостях параллельных данной неподвижной плоскости.

-угол между фиксированной прямой, проходящей через полюс и осью абсцисс.

X ,Y – координаты полюса.

10)М.Ц.С. , М.Ц.У. Способы их определений.

М .Ц.С. фигуры – это точка, принадлежащая фигуре или неизменно с ней связанная, скорость которой в данный момент времени равна нулю.

М .Ц.У. фигуры – это точка неизменно связанная с твёрдым телом, движущемся плоско – параллельно, ускорение которой в данный момент времени равно нулю.

11)Сложное движение точки. Абсолютная, относительная и переносная скорости и ускорения точки.

1)Сложное движение точки – это такое движение точки тела, которое рассматривается одновременно в двух системах отсчёта: в подвижной системе отсчёта и неподвижной.

2)Абсолютная скорость и ускорение – это скорость и ускорение точки относительно неподвижной системы отсчёта.

Абсолютное движение – это движение точки относительно неподвижной системы отсчёта.

3)Относительная скорость и ускорение – это скорость и ускорения точки в её относительном движении.

Относительное движение точки – это движение точки относительно подвижной системы отсчёта.

4)Переносные скорость и ускорение – это скорость и ускорение точки в её переносном движении.

Переносное движение точки – это движение точки неизменно связанное с подвижной системой отсчёта относительно неподвижной системы отсчета.

Т еорема: Абсолютная скорость точки определяется векторной суммой, её относительной скорости и переносной скорости.

12)Теорема Кориолиса.

П олное (абсолютное) ускорение точки при её сложном движении определяется геометрической суммой трёх векторов ускорений: переносного (We), относительного (Wr) и Кориолисова (Wk) ускорений.

М одуль Кориолисова ускорения:

Направление Кориолисова ускорения определяется как правая тройка векторов.

Построение Кориолисова ускорения:

1 3)Кинематический винт.

Это совокупность поступательного и вращательного движения тела при условии, что угловая скорость вращения параллельна скорости поступательного движения. При этом ось вращения  назавается винтовоя осью. (при этом движение называется правовинтовым, если угловая скорость и скорость поступательного движения одинаково направлена; и левовинтовым, если они противоположны)

Шагом винта называется расстояние, которое проходит т.N за один полный оборот.

1)Аксиомы статики.

1)Аксиома инерции: Материальное тело под действием уравновешенной системы сил, находится в состоянии равновесия или прямолинейного равномерного движения.

2)Аксиома двух равных сил: Система из двух сил называется уравновешенной, если силы равны по модулю, лежат на одной прямой и противоположны по направлению.

3)Аксиома присоединения и исключения уравновешенной системы сил: Действие системы сил на тело не изменится, если к ней добавить или исключить уравновешенную систему сил.

4)Аксиома параллельных сил: Равнодействующая двух сил, приложенных в одной точке тела равна их геометрической сумме, и приложена к той же точке.

5)Аксиома равенства действия и противодействия: Два тела взаимодействуют между собой с силами равными по модулю и противоположно направленными.

Они не являются уравновешенными, т.к. приложены к разным телам.

6)Аксиома отвердевания: Состояние равновесия деформируемого тела не изменится, если считать это тело абсолютно твёрдым.

7)Аксиома связи: Любое не свободное тело можно рассматривать как свободное, если исключить связи, заменив их действие на тело реакциями связи.

2)Геометрический и аналитический способы определения равнодействующей системы сходящихся сил.

Г еометрический способ:

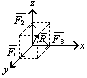1) 2) 3)

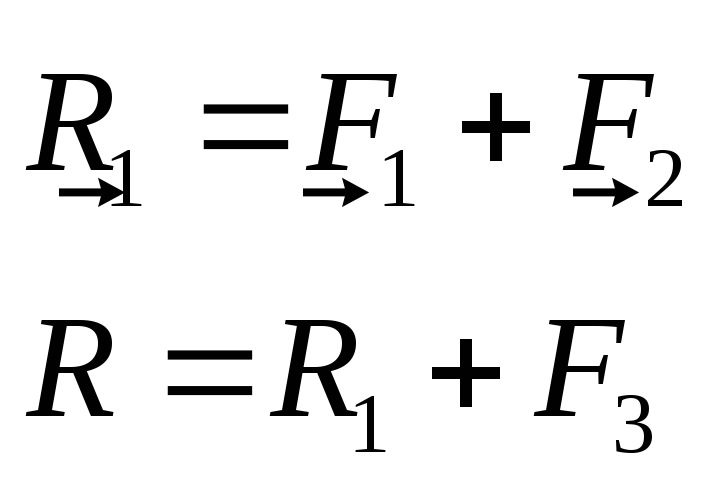
А налитический способ:

М одуль: Направления:

Д ля сил находящихся на одной плоскости:

3)Момент силы относительно центра и относительно оси.

М омент силы относительно центра – есть вектор, приложенный в этой точке и направленный перпендикулярно плоскости, в которой лежит вектор силы и центр так, что глядя против направления вектора момента силы, вращение силы наблюдается против часовой стрелки.

М омент силы относительно оси – скалярная величена определяемая произведением проекции силы на плоскость перпендикулярную оси на плечё проекции силы относительно пересечения плоскости с осью.

4)Пара сил, её момент.

П ара сил – это такая система двух равных по модулю, параллельных и противоположно направленных сил, линии, действия которых не совпадают.

Момент пары сил – это вектор, модуль которого определяется произведением модуля одной из сил пары на плечё пары, направленный перпендикулярно плоскости, в которой лежат линии действия пары и направленный так, что глядя против его направления, вращение пары наблюдается против часовой стрелки.

5)Теоремы: 1)О равновесии трёх непараллельных сил. 2)О параллельном переносе силы. Метод Пуансо. 3)О приведении произвольной системы сил к данному центру. 4)О моменте равнодействующей.

1)О равновесии трёх непараллельных сил: Если система из трёх непараллельных уравновешенных сил лежащих в одной плоскости действует на твёрдое тело, то линии действия их пересекаются в одной точке.

2)О п араллельном переносе силы. Метод Пуансо: Действие силы на твёрдое тело не изменится, если переместить её параллельно самой себе в любую другую точку твёрдого тела, при этом добавить момент пары сил, равный по модулю моменту силы относительно новой точки её приложения.

3)О приведении произвольной системы сил к данному центру: Произвольную пространственную систему сил можно привести к главному вектору, приложенному в центре приведения и главному моменту системы сил определяемому как векторная сумма моментов всех сил относительно того же центра приведения.

4)О моменте равнодействующей: Момент равнодействующей системы сил в центре приложения равен геометрической сумме моментов всех сил относительно точки приведения.

6)Центр параллельных сил. Центр тяжести.

Определение: Центр параллельных сил – это точка, через которую проходит равнодействующая системы параллельных сил, одинаково направленная при одновременном повороте всех сил системы на один и тот же угол, в одну и туже сторону вокруг их точки приложения.

Ц ентр тяжести для однородного тела:

Vi - элементарные объёмы определённых частиц. Xc, Yc, Zc – координаты ц.т.

Ц ентр тяжести:

Pi - сила веса отдельной частицы.

Ц ентр параллельных сил:

Fi - модуль соответствующей силы системы.

Ц .т. через радиус-вектор: Радиус-вектор начин. в начале коорд. и закан. в ц.т.

7)Динамический винт. Произвольную систему сил можно привести к одной силе и к вектору момента, модуль которого равен моменту пары лежащей в плоскости перпендикулярной вектору сил, такая совокупность результирующей силы и вектора момента называется динамическим винтом.

ТЕОРЕМЫ:

Сложение 2-х || направленных в одну и противоположенные стороны. Теорема. Модуль равнодействующей 2-х || направленных в одну и туже сторону = сумме их модулей. Линия действия равнодействующей проходит между т. приложения этих сил на расстоянии обратно проп. Модулям этих сил. Модуль равнодействующей 2-х || разных по модулю противоположно направленных сил = разности модулей этих сил. Равнодействующая направлена также как и большая по модулю сила а линия действия равнодействующей R проходит вне отрезка соединяющего т. приложения || сил на расст. От точек приложения сил обратно проп. Модулям приложенных сил.

Теорема об эквивалентности пар. Теорема 1. 2 пары эквивалентны если они лежат в одной пл-ти и их моменты равны. Теорема 2. 2 пары сил явл. Эквивалентными если их векторы моментов равны. Действие пары сил на тв. Тело не измен. если эту пару перенести в пл-ть || исходной пл-ти действия пары.

Теорема Вареньёна или о моменте равнодействующей. Момент равнодействующей { сил относит.центра = геом. сумме моментов всех сил { относит того же центра приведения.

Определение неподвижного центроида. Неподвижная центроида- геометрическое место точек совпадающее в данный момент с мгн центром скоростей и принадлежит неподвижной поверхности. Подвижная центроида- геом место точек совпадающее в данный момент с мгн центром скоростей в данный момент времени движущегося тела.

Движение тв тела вокруг неподвижной т. (сферическое движение). Сферическое движение- такой вид движения при котором одна т неизменно связанная с телом остаётся неподвижной в процессе всего движения.

Теорема Эйлера-Даламбера. Любое перемещение при сферическом движении тв тела можно задать одним его поворота вокруг оси проходящей через неподвижную точку.

Общие случаи движения свободного твёрдого тела. Перемещение при произвольном движении свободного твёрдого тела всегда можно заменить суммой двух перемещений: перемещение тела вместе с полюсом при его поступательном движении и повороте этого тела вокруг оси вращения, проходящей через полюс.

ОПРЕДЕЛЕНИЯ:

Теор. Мех.- естественная наука, изуч законы движения и условия равновесия материальных тел под действием приложенных к ним сил.

Движение в механике- механическое движение, т.е. изменение положения тел в пространстве с течением времени.

Механическое взаимодействие- тот вид взаимодействия между материальными телами, в результате, которого изменяется состояние движения тел или их форма (т.е. они деформируют).

Тело- векторная величина являющаяся количественной мерой механического взаимодействия. сист. сил- совокупность сил действующих на тело.

Линия действия силы - прямая вдоль которой действует сила.

Эквивалентные сист. сил- 2 сист. сил при замене действия на тело одной сист.сил другой сист. сил в состоянии движения тела при такой замене не изменится.

Равнодействующая сила- сила при которой одна сила заменяет действие на тело сист. сил.

Уравновешивающая сила- сила равная по модулю равнодействующей действующей по одной прямой и направлена в противоположную сторону.

Сосредоточенная сила- сила, приложенная в любой точке тела.

Распределённые силы- силы приложенные ко всем частицам объёмного тела или части его поверхности.

Внешние силы- силы приложенные к частицам одного тела со стороны другого тела.

Внутренние силы- силы приложенные к частицам тела со стороны частиц этого же тела (силы возникают между частицами одного и того же тела). Внутренние силы являются уравновешенными, поэтому при рассмотрении равновесия тела их можно исключить из рассмотрения. Несвободное тело- перемещение, которого ограничено в пространстве опорами или связью.

Свободное тело- тело, которому можно сообщить перемещение в любом направлении пространства.

Реакции опоры- сила, которая полностью заменяет действие связи или опоры на тело.

Виды опор. Гладкая опора - такая поверхность, трением тела, о которую пренебрегаем. Такая поверхность запрещает движение тела вдоль общей нормали. При этом сила реакции направлена вдоль нормали точки касания тела и приложена в этой точке.

Нерастяжимая нить реакция нити направлена вдоль нити к точке подвеса.

Цилиндрический шарнир (шарнир- устройство, скрепляющее тела позволяющее вращение относительно друг друга)- позволяет вращение тел и скольжение вдоль неё. Реакция шарнира направлена произвольно в пл-ти перпендикулярной оси вращения.

Сферический шарнир- устройство, имеющее одну неподвижную точку вокруг которой может происходить произвольное вращение связанных тел. Если шарнир имеет упорную пл-ть, то он называется подпятник.

Главный вектор сист. сил - вектор, определяющийся геометрической суммой всех сил системы.

Главный момент системы сил - определяется моментом пары сил, который равен векторной сумме моментов всех сил системы относительно центра приведения.

Центр приведения - точка относительно которой определяется момент системы сил и точка в которой приложен главный вектор системы сил.

Кинематика- раздел теор мех изуч геом св-ва движения тел без учёта их массы и причин создающего движение.

Сист. отсчёта- система координат закреплена на одном из тел окруж движение которое рассм. и время.

Нормальная пл-ть- пл-ть перпендикулярная соприкасающейся пл-ти и кас.

Главная нормаль- Линия пересекающая нормальную и соприкасающуюся пл-ти. Соприкасающаяся пл-ть- пл-ть проходящая через точку и касательную линию.

Поступательное движение твёрдого тела- движение тела при котором прямая соединяющая любые две его точки перемещается || самой себе

Неподвижная центроида – геометрическое место точек, совпадающее в данный момент с М.Ц.С. и принадлежащее неподвижной поверхности.

Подвижная центроида – геометрическое место точек, совпадающее в данный момент с М.Ц.С. движущегося тела.

Сферическое движение – это такой вид движения при котором одна точка неизменно связанная с телом остаётся не подвижной в процессе всего движения.

Д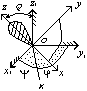 ля задания сферического движения выберем две системы отсчета подвижную и неподвижную при этом начало систем отсчёта совмещены с неподвижной точкой тела (т.О). Линия пересечения плоскостей OXY и OX1Y1 это линия OK называется линией узлов.  - угол собственных вращений, т.е. угол между линией узлов OK и осью OX подвижной системой отсчёта.;  - угол прицессии. Угол между линией узлов и осью OX1 неподвижной системы отсчёта; Q – угол нутации. Угол между осями OZ и OZ1. Все эти углы (,, Q) углы Эйлера.

Общие случаи движения свободного твёрдого тела – движение при котором твёрдое тело движется как угодно произвольно относительно системы отсчёта.

Неподвижный аксоид – геометрическое место мгновенных осей вращения при сферическом движении твёрдого тела в неподвижной системе отсчёта.

Подвижный аксоид – геометрическая поверхность, образоваееая последовательным занятия положения мгновенных осей вращения твёрдого тела при его сферическом движении в подвижной системе отсчета.

У гловая скорость твёрдого тела при его сферическом движении – есть вектор, направленный вдоль мгн.оси вращения таким образом что глядя с конца вектора вращение тела наблюдается против часовой стрелки, а модуль этого вектора равен: