Скорость в векторном

Скоростью точки в данный момент времени называется вектор v, равный первой производной от ее радиуса-вектора r по времени:

v = dr/dt = ; (Производную по времени принято в механике обозначать точкой над дифференцируемой величиной).

Вектор скорости, характеризующий изменение с течением времени модуля и направления радиуса-вектора точки, направлен по касательной к траектории точки в сторону ее движения.

При прямолинейном движении вектор скорости v все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь по величине; при криволинейном движении кроме модуля все время изменяется и направление вектора скорости точки.

В качестве единиц измерения скорости применяют обычно м/с или км/ч.

Ускорение в векторном

Ускорением точки в данный момент времени называется вектор a, равный первой производной от вектора скорости v или второй производной от ее радиуса-вектора r по времени:

a = dv/dt = dr2/dt2 ; или a = =.

Ускорение точки, как векторная величина, характеризует изменение с течением времени модуля и направления вектора скорости точки.

Рассмотрим, как располагается вектор a по отношению к траектории точки. При прямолинейном движении вектор a направлен вдоль прямой, по которой движется точка. Если траекторией является пространственная кривая, то вектор a направлен в сторону вогнутости траектории и лежит в соприкасающейся плоскости. Так называют плоскость, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении dr = vdt движущейся точки (подробнее это понятие изложено при задании движения точки естественным способом). Для пространственной кривой в каждой ее точке будет, вообще говоря, своя соприкасающаяся плоскость. Для плоской кривой соприкасающаяся плоскость совпадает с плоскостью этой кривой и является общей для всех ее точек.

В качестве единицы измерения ускорения применяется обычно м/с2.

скорость любой точки плоской фигуры в плоской движении, равна геометрической сумме скорости полюса и скорости рассматриваемой точки при вращении фигуры вокруг полюса.

Теорема. Проекции скоростей точек плоской фигуры на ось, проходящую через эти точки, равны.

Мгновенный центр ускорений

Α=arctg(ε/ω2)

WQ=0

WAτ= εAQ, WAn= ω2 AQ,

WA=√( WAτ)2+( WAn)2= AQ√ε2+ ω2

tgα= WAτ/ WAn= ε/ ω2

Частный случай:

1)ε=0, тогда α=0

2)ω=0, тогда α=π/2 (дв-е мгновенно поступательное)

Мгновенный центр ускорений – точка (Q) плоской фигуры, ускорение которой в данный момент времени равно нулю. Для его построения из точки А откладываем под углом к ускорению а_А отрезок , при этом угол откладывается от ускорения в сторону, направления углового ускорения. Модули ускорений точек плоской фигуры пропорциональны расстояниям от этих точек до мгн.ц. ускорений, а векторы ускорений составляют с отрезками, соединяющими эти точки и м.ц.у. один и тот же угол :.

Сложное движение точки (тела)

– такое движение, при котором точка (тело) одновременно участвует в нескольких движениях (напр. пассажир, перемещающийся по движущемуся вагону). В этом случае вводится подвижная система координат (Oxyz), которая совершает заданное движение относительно неподвижной (основной) системы координат (O₁x₁y₁z₁).

Теорема о сложении скоростей: ,;

-орты (единичные вектора) подвижной системы координат, орт вращается вокруг мгновенной оси, поэтому скорость его конца и т.д.,: ,

; – относительная скорость.

; переносная скорость: , поэтому абсолютная скорость точки = геометрической сумме ее переносной (v_e) и относительной (v_r) скоростей , модуль:.

Теорема о сложении ускорений (теорема Кориолиса):

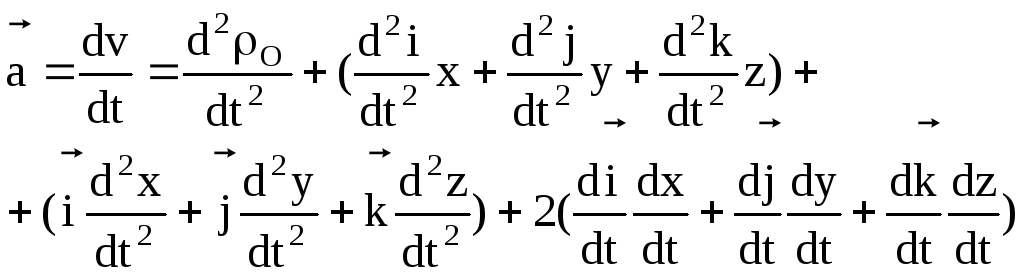
и т.д. Слагаемые выражения, определяющего ускорения :

1) – ускорение полюса О;

2)

3) – относительное ускорение точки;

4) ,

получаем: .

Первые три слагаемых представляют собой ускорение точки в переносном движении: – ускорение полюса О; – вращательное уск., – осестремительное уск., т.е. . Теорема о сложении ускорений (теорема Кориолиса): , где – ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки из-за ее относительного движения; 2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса: а_с= 2|_ev_r|sin(_e^{^}v_r), направление вектора определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90^о в направлении вращения.

Кориолисово уск. = 0 в трех случаях: 1) _e=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) v_r=0; 3) sin(_e^{^}v_r)=0, т.е. (_e^{^}v_r)=0, когда относительная скорость v_r параллельна оси переносного вращения. В случае движения в одной плоскости – угол между v_r и вектором _e = 90^о, sin90^o=1, а_с=2_ev_r.