
- •Сопротивление материалов – заочно Примеры решения задач Задача 1. Стержневая система
- •Задача 2. Статически неопределимая стержневая система
- •Задача з. Теория напряженного состояния
- •Задача 4. Кручение
- •Задача 5. Геометрические характеристики плоских сечений
- •Задача 6. Плоский изгиб
- •Задача 8. Внецентренное сжатие
- •Задача 9. Изгиб с кручением
Сопротивление материалов – заочно Примеры решения задач Задача 1. Стержневая система
Два стальных стержня, шарнирно соединенных в точке А, находятся под действием силы Р .Первый стержень имеет длину с и площадь поперечного сечения F, второй длину a и площадь 2F.
|
|
Требуется найти: 1) величину нормальный напряжений, действующих в стержнях. 2) абсолютную и относительную деформации стержней. Исходные данные: Р = 130 кН,с = 1,5 м,а = 2 м,F = 12 см^2. Решение. Стержни прикреплены к стене и соединены между собой шарнирами (точках В ,С иА ). Шарниры предполагаются идеальными, т. е. такими, трение в которых отсутствует. НагрузкаР приложена в узлеА . Поэтому стержни будут испытывать только продольные (растягивающие или сжимающие) усилия, т.е. в поперечных сечениях стержней возникает только один внутренний силовой фактор - продольная силаN . 1. Для определения усилий используем метод сечений .Рассечем стержни,отбросим часть, содержащую опорные точки.Заменяя действие отброшенной части, приложим в сечениях неизвестные продольные усилияN 1 иN 2 .Полагая оба стержня растянутыми, направим усилияN 1 , иN 2 так, как показано на рис.(1.2). |
Уравновесим отсеченную часть. Для сходящейся плоской системы сил можно составить два независимых уравнения равновесия - в виде сумм проекции всех сил на две осих иу (рис. 1.2).
Тогда уравнения равновесия представятся в виде:

Для определения
![]() и
и![]() рассмотрим
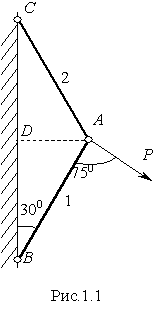
стержневую систему(рис.1.1). Из
точкиА опустим перпендикулярА
D на прямуюВС , получим два
прямоугольных треугольникаABD иАDC .
рассмотрим
стержневую систему(рис.1.1). Из
точкиА опустим перпендикулярА
D на прямуюВС , получим два
прямоугольных треугольникаABD иАDC .
|
|
Из треугольника ABD определимAD :
Из треугольника AD С получим:
Теперь определим неизвестные усилия N 1 , иN 2 из системы двух линейных уравнений(1.1). Перепишем уравнения в следующем виде: |
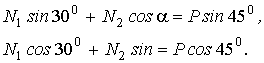 (1.2)
(1.2)
Решим систему (1.2), используя, например, метод Крамера.
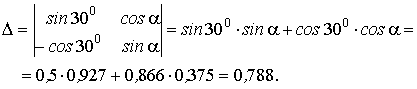
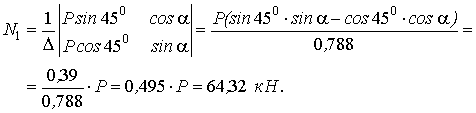
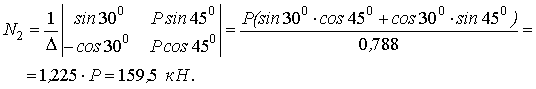
2. Определим нормальные напряжения, действующие в стержнях.
Напряжения в стержнях определяются по формуле
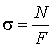
Для первогостержня
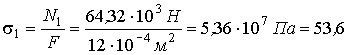 МПа,
МПа,
для второгостержня
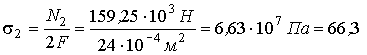 МПа,
МПа,
3. Найдем абсолютную и относительную деформации стержней.
Абсолютная деформация стержня длиной lопределяется из закона Гука:
![]()
Абсолютная деформация первого стержня
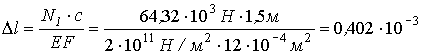 м.
м.
Абсолютная деформация второго стержня
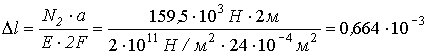 м.
м.
Относительную деформацию определим из закона Гука
![]() .
.
Относительная деформация первого стержня
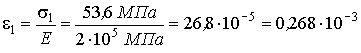 ,
,
относительная деформация второго стержня
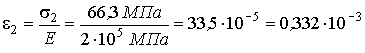 .
.
Литература: 1 § 1.2 – 8.2
![]()
Задача 2. Статически неопределимая стержневая система
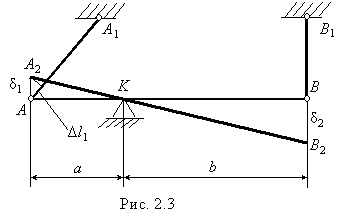
Абсолютно жесткий брус шарнирно закреплен на неподвижной опоре и поддерживается двумя стержнями (рис. 2.1).
|
|
Требуется найти: 1)
усилия и напряжения в стержнях, выразив
их через силу
2)
допускаемую нагрузку [
3)
предельную грузоподъемность системы
Q пр и допускаемую нагрузку [Q
пр ], если предел текучести 4) сравнить величины допускаемых нагрузок [ Q ] и [Q пр ]. Исходные данные: а = 2,1 м,b = 2,4 м,с = 1,5 м,F = 12см 2 . |
Решение.
|
|
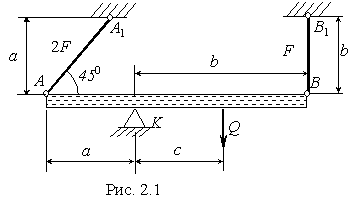
1. Рассечем стержни АА 1 иВВ 1 , усилияN 1 , иN 2 в стержняхАА 1 , иВВ 1 , направим вдоль осей стержней как показано на рис.2.2. Реакция опорыК имеет горизонтальную составляющуюН К , и вертикальную составляющуюR К , так как эта опора препятствует горизонтальному и вертикальному перемещению точкиК бруса. Таким образом, всего имеется четыре неизвестные реакции (рис.2.2), а независимых уравнений равновесия для плоской системы сил можно составить всего три. Следовательно, данная система один раз статически неопределима Статически неопределимые системы рассчитывают путем совместного решения уравнений, полученных в результате рассмотрения статической, геометрической и физической сторон задачи. |
Статическая сторона задачи. По условию задачи необходимо определить усилияN 1 иN 2 , a в определении реакцийН К иR К нет необходимости. Поэтому достаточно из трех возможных уравнений равновесия использовать одно, в которое не входили бы реакцияН К иR К . Таким является уравнение суммы моментов всех сил относительно шарнираК :
![]()
где
![]() (м).
(м).
Подставляя в уравнение значения h ,b ис , получим
![]() (2.1)
(2.1)
Геометрическая сторона задачи .
Под действием внешней силы
![]() абсолютно
жесткий брус повернется вокруг точкиК . ШарнирыА иВ после
деформации переходят в положениеА
2 иВ 2 соответственно, т.е.
перемещаются по вертикали на величины
абсолютно
жесткий брус повернется вокруг точкиК . ШарнирыА иВ после
деформации переходят в положениеА
2 иВ 2 соответственно, т.е.
перемещаются по вертикали на величины![]() 1
и
1
и![]() 2(рис.2.3).
2(рис.2.3).
|
|
Из подобия треугольников AA 2К иВВ 2К находим
Выразим
укорочение
|
откуда
|
|
или с учетом равенства (2.2) |
|
Физическая сторона задачи . Используя закон Гука, записанный для абсолютных деформаций, выразим деформации стержней через усилия
|
|
|
|
Подставим выражения (2.3) в условие (2.4) |
|
|
после сокращения получим |
|
Решаем совместно уравнения статики (2.1) и уравнение(2.5):

![]()
Определяем напряжения в стержнях 1 и 2:
|
|
|
2. Найдем допускаемую нагрузку [![]() ], приравняв большее по модулю
напряжение допускаемому напряжению
], приравняв большее по модулю
напряжение допускаемому напряжению![]() =
160 МПа.
=
160 МПа.
|
|
откуда |
|
3. Найдем нагрузки предельную - Q пр и
допускаемую - [Q пр ], если предел
текучести![]() Т = 240 МПа и запас прочностиn = 1,5.
Т = 240 МПа и запас прочностиn = 1,5.
При увеличении нагрузки Q c верх
значения [Q ] напряжения в обоих
стержнях сначала увеличивается прямо
пропорционально нагрузке. При увеличении
нагрузки до некоторой величиныQ >
[ Q ] напряжение![]() 2 во втором стержне достигают предела
текучести
2 во втором стержне достигают предела
текучести![]() Т
, а усилиеN 2 - предельного значенияN 2пр =
Т
, а усилиеN 2 - предельного значенияN 2пр =![]() Т
·F . При этом напряжение
Т
·F . При этом напряжение![]() 1
сжатия в первом стержне остается меньше
1
сжатия в первом стержне остается меньше![]() Т
. При дальнейшем увеличении нагрузки,
напряжения во втором стержне остаются
постоянными, равными пределу текучести,
а в первом - возрастают, пока также не
достигают
Т
. При дальнейшем увеличении нагрузки,
напряжения во втором стержне остаются
постоянными, равными пределу текучести,
а в первом - возрастают, пока также не
достигают![]() Т
, усилиеN 1 при этом равно
Т
, усилиеN 1 при этом равно
N 1пр = –![]() Т
·2F . Это состояние системы называется
предельным, соответствующим исчерпанию
ее грузоподъемности. Дальнейшее, даже
незначительное увеличение нагрузки
связано с весьма большими деформациями
системы. Величину силыQ , вызываюшую
предельное состояние, обозначаютQ
пр и называют предельной силой.
Т
·2F . Это состояние системы называется
предельным, соответствующим исчерпанию
ее грузоподъемности. Дальнейшее, даже
незначительное увеличение нагрузки
связано с весьма большими деформациями
системы. Величину силыQ , вызываюшую
предельное состояние, обозначаютQ
пр и называют предельной силой.
Для вычисления Q пр подставим в уравнение (2.1) значения предельных продольных усилий, возникающих в стержняхN 1 =N 1пр ,N 2 =N 2пр :
|
|
откуда |
|
|
|
|
4. Сравним величины допускаемых нагрузок [ Q ] и [ Q пр ] |
|
Литература: 1, §9.2.
![]()

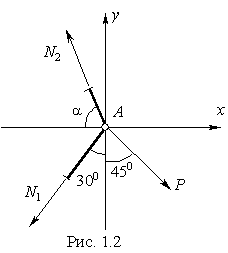
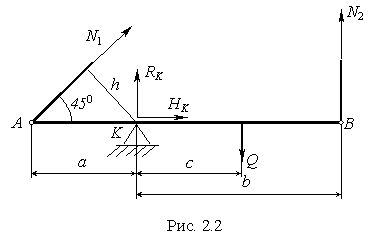
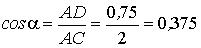 ,
,
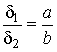 (2.2)
(2.2)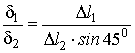
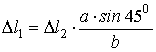 (2.3)
(2.3)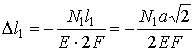
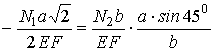
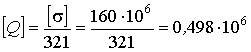 Н.
Н.
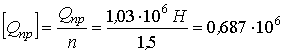 Н.
Н.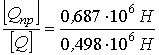 =
1,38.
=
1,38.