Глава 6. Аксонометрические проекции

6.1. Классификация аксонометрических проекций

Аксонометрической проекцией (или аксонометрией) называется наглядное изображение геометрического тела, полученное в результате параллельного проецирования его на некоторую плоскость, называемую плоскостью аксонометрических проекций (или картинной плоскостью), вместе с осями прямоугольных координат, которые определяют положение этого тела в пространстве (рис. 6.1).

При этом для обеспечения наибольшей наглядности изображения необходимо правильно выбрать направление аксонометрического проецирования Sa, т. е. обеспечить видимость наибольшего числа элементов тела.

Аксонометрические изображения используют в технической документации для получения наиболее полного представления о форме предмета, однако при этом все ребра и грани полученной модели имеют искаженные размеры и форму, что затрудняет определение истинных размеров предмета.

Аксонометрическая проекция, полученная при прямоугольном проецировании на картинную плоскость, называется прямоугольной. Аксонометрическая проекция, полученная при выполнении проецирования на картинную плоскость под любым другим углом, называется косоугольной.

При косоугольном проецировании (в отличие от прямоугольного проецирования) происходит искажение пропорций отдельных частей тела, что неприемлемо при решении инженерных задач.

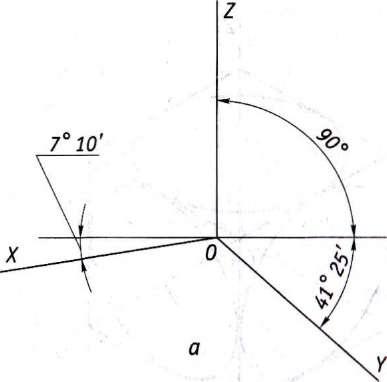
Оси пространственной системы координат, в которой находится рассматриваемый объект, спроецированные на картинную плоскость а (рис. 6.2), называются аксонометрическими.

В зависимости от взаимного расположения осей координат, картинной плоскости и направления проецирования отрезки, откладываемые на осях, например х, у, z — координаты точки А, проецируются на картинную плоскость с различным искажением:

x1/x=k; y1/y=m; z1/z=n.

Рис. 6.1

Отношения к, т, п отрезков на аксонометрических осях к отрезкам на координатных осях называются коэффициентами искажений координат.

В случае равенства отрезков, откладываемых на координатных и аксонометрических осях, коэффициенты к, т,п равны единице и называются приведенными, а масштабы искажений — аксонометрическими.

По соотношению общих размеров тела и его изображения ак­сонометрические проекции подразделяются на две группы: нормальные (точные) и увеличенные.

Нормальные изображения получают при непосредственном аксонометрическом проецировании. При этом масштабы искажений по координатным осям будут в общем случае дробными числами, что затрудняет вычисление размеров тела и построение аксонометрического изображения.

Увеличенные аксонометрические изображения получают из нормальных изображений, пропорционально увеличивая их раз меры в целях упрощения аксонометрических масштабов, при этом масштабы искажений по координатным осям могут быть целыми числами, что упростит вычисление размеров и построе­ние аксонометрического изображения элементов тела.

Для показа внутреннего устройства тела в аксонометрии при­меняют разрезы, которые получают путем мысленного его рассе­чения плоскостями, параллельными основным плоскостям про­екций, и условного удаления соответствующей (передней) части.

Штриховка сечений в аксонометрии выполняется параллель­но одной из диагоналей проекций квадратов, построенных на ак­сонометрических осях.

Размеры на аксонометрических проекциях не проставляются.

Рассмотрим наиболее распространенные аксонометрические проекции.

Можно выделить три основных вида положений координатных осей тела на аксонометрической проекции: изометрические — все три оси имеют одинаковый масштаб искажений; диметрические — две оси имеют одинаковый масштаб, а третья отличается от них; триметрические — все три оси имеют различные масш­табы искажений.

Прямоугольная изометрическая проекция. Эта проекция наиболее наглядна, она чаще других проекций используется в практических построениях и вносит наименьшее число искажений.

Рис. 6.2

Рис. 6.3

В прямоугольной изометрической проекции все коэффициен­ты искажений равны между собой, т.е. к = т = п = 0,82. Для уп­рощения построения аксонометрической проекции принимают к=т=п=1, получая при этом изображение предмета, увеличен­ное в 1,22 раза.

В данной проекции координатная система осей, грани куба и окружности, вписанные в грани куба, проецируются на аксоно­метрическую плоскость так, как показано на рис. 6.3. Все три по­лучаемые при этом эллипса одинакового размера: их большие оси, перпендикулярные аксонометрическим осям, равны 1,22 диа­метра окружности, а малые оси, совпадающие с аксонометриче­скими осями, равны 0,71 диаметра окружности.

Прямоугольная диметрическая проекция. В этой проекции предпочтительно строить изображения удлиненных тел.

В прямоугольной диметрической проекции коэффициенты ис­кажения по осям Хи Z равны 0,94, а по оси Y— 0,47. Для упро­щения построения коэффициенты искажений по осям Х и z при­нимают равными 1, а по оси Y — 0,5, при этом получая изобра­жение предмета, увеличенное в 1,06 раза.

В данной проекции координатная система осей, грани куба и окружности, вписанные в грани куба, проецируются на аксоно­метрическую плоскость так, как показано на рис. 6.4. Получае­мые при этом эллипсы 1 и 3 одинакового размера: их большие оси, перпендикулярные аксонометрическим осям, равны 1,06 диаметра окружности, а малые оси,

совпадающие с аксонометри­ческими осями, равны 0,35 диаметра окружности. Малая ось эл­липса 2 равна 0,95 диаметра окружности.

Косоугольная фронтальная диметрическая проекция. Ис­пользуется в тех случаях, когда на чертеже имеется множество ок­ружностей (например, отверстий), расположенных на плоскостях, параллельных фронтальной плоскости. Эти окружности на аксо­нометрической проекции изображаются без искажений, что зна­чительно упрощает построения.

Коэффициенты искажения по осям Х и Z принимаются здесь равными 1, а по оси Y— 0,5.

В данной проекции координатная система осей, грани куба и окружности, вписанные в грани куба, проецируются на аксоно­метрическую плоскость, как показано на рис. 6.5. Окружность, находящаяся в плоскости, параллельной фронтальной плоскости проекций, проецируется в виде окружности, а окружности, лежа­щие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, — в виде эллипсов, большие оси которых равны 1,07, а малые — 0,33 диаметра проецируемой окружности.

В косоугольной фронтальной диметрической проекции допус­кается наклон оси Y на угол 30° или 60°.