Контрольные вопросы

1. Какие стандартные технологии являются однотипными для вычислительных систем?

2. Чем отличается работа конструктора на бумаге от его работы на компьютере?

3. Какие графические примитивы используют для построения двухмерного изображения чертежа?

4. Зачем необходимы вспомогательные линии построения?

5. Чем отличаются команды LINE и XLINE?

6. Зачем необходима на чертеже точка?

7. Как построить окружность на экране компьютера?

8. Как осуществляется редактирование чертежа на компьютере?

9. Является ли процесс указания размеров на чертеже автоматическим?

10. Чем различаются между собой каркасные, поверхностные и твердотельные модели?

11. Какие исходные тела формируются в AutoCAD?

12. Аналогичны ли ввод и редактирование двухмерных и трехмерных объектов?

13. Почему необходимо выбирать различные направления проециро­вания при визуализации объектов?

14. Как можно увеличить реалистичность изображения объектов?

17.5. Перспективные технологии конструирования объектов сложной формы

Конструирование изделий сложной геометрической формы в современных графических приложениях, где в основном используются векторные модели, весьма трудоемкая задача, требующая мною времени и вычислительных ресурсов.

Применение алгебраических моделей высших порядков значительно снижает (см. гл. 16) объемы записи проектируемых объектов в память компьютера.

Перспективные алгебраические модели высших порядков обеспечивают применение новых технологий конструирования поверхностей сложной геометрической формы, основанных на изменении значений коэффициентов алгебраического уравнения.

Рассмотрим эти технологии.

Модификация коэффициентов. Это один из методов конструирования поверхностей сложных форм посредством изменения коэффициентов алгебраических уравнений высших порядков. Этот метол позволяет создавать многообразные формы, так как изменять можно любые коэффициенты и каким угодно образом, однако для его практической реализации необходимо провести исследование форм, получаемых при изменении различных коэффициентов.

Метод модификации коэффициентов алгебраического уравнения состоит в плавном последовательном изменении числовых значений каждого из коэффициентов этого уравнения в целях по­лучения новых поверхностей.

Так как переменные в уравнениях высших порядков имеют сложные нелинейные зависимости, то управление формой поверхности посредством изменения даже одного коэффициента такого уравнения может привести к получению неузнаваемого (недействительного) изображения.

Практика показала, что формирование форм поверхностей посредством изменения коэффициентов уравнений включает в себя сложные зависимости, которые неадекватны при переходе от одного коэффициента к другому, от одной поверхности к другой.

Рис. 17.3 Рис. 17.4

Для исследования влияния значений коэффициентов алгебраических уравнений от 1 -го по 4-й порядок была разработана компьютерная программа формирования и визуализации алгебраических поверхностей. Вид панели ввода данных в эту программу представлен на рис. 17.2.

Выбрав порядок поверхности и вводя различные положитель­ные, нулевые или отрицательные числовые десятичные значения коэффициентов соответствующего алгебраического уравнения, получают отображение этой поверхности на экране, которое мож­но рассматривать с любой стороны, масштабировать, переметать и врашать вокруг любой оси системы координат

Рассмотрим примеры модификации коэффициентов алгебраических уравнений с помошью этой программы.

Возьмем поверхность 4-го порядка в виде пересекающихся сфер (см. рис. 16.20), уравнение которой имеет вид

х4 +y4 + z4+ 2x2y2+ 2x2z2 - 10х2 - by2 – 6y2 -6z2 + 9 = 0.

Будем изменять значения коэффициентов исходного уравне­ния.

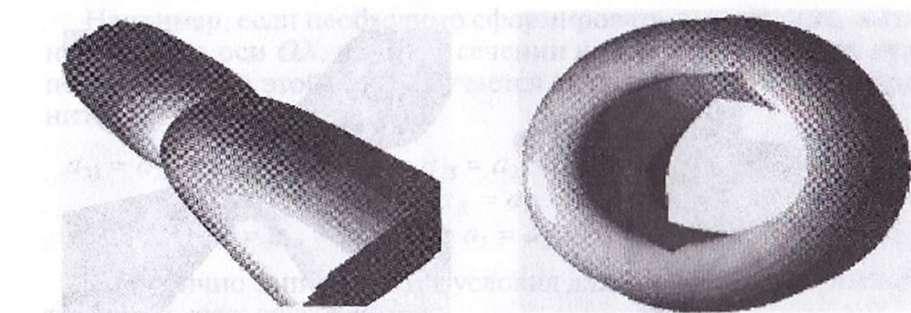
Если коэффициент при х4, равный 1, изменить на 0, получим новую поверхность 4-го порядка в виде перетянутой трубки (рис. 17.3).

Если коэффициент при х4, равный 1. изменить на 4, получим новую поверхность в виде самодельного кольца (рис. 17.4).

Если коэффициент при x2y2, равный 2, изменить на -1, полу­чим поверхность в виде бабочки (рис. 17.5).

Если коэффициент при x2z2 равный 2, изменить на -3, полу­чим новую поверхность в виде пропеллера (рис. 17.6),

Если коэффициент при x2z2, равный 2, изменить на +12, по­лучим поверхность в виде специальной прокладки (рис. 17.7).

Если коэффициент при y2y2, равный 2, изменить на -3, полу­чим поверхность в виде морской звезды (см. рис. 16.23).

Если коэффициент при y2z2, равный 2, изменить на 11, полу­чим поверхность в виде разорванной сферы (рис. 17.8).

Рис. 17.5 Рис. 17.6

Исследования показали, что переход знака коэффициентов уравнений высоких степеней может привести к образованию новой формы поверхности или ее исчезновению. Изменение значений коэффициентов уравнений низших степеней приводит к сглаживанию формы образованной поверхности и стыковки ее с другими поверхностями.

Изменением коэффициентов при различных переменных можно управлять, изменяя формы поверхности в объеме к направлении осей системы координат.

Конструирование симметричных поверхностей. Этот метол основывается на факторе проецирования отдельных геометрических свойств поверхности на коэффициенте уравнения.

Метод заключается в использовании уравнения плоской кривой для формирования тела вращения или цилиндрической поверхности с постоянным сечением сложной формы.

Рис. 17.7

Например, если необходимо сформировать поверхность, вытянутую вдоль оси ОХ, в любом сечении которой плоскостью, перпендикулярной этой оси, получается эллипс, необходимо выполнить следующее условие:

a₃₃ = a₃₂ = a₃₁ = a₃₀ = a₂₉ = a₂₈ = a₂₇ = a₂₆ = _a25 = a₂₄ = a₂₃ = a₂₂ = a₂₁ = a₂₀ = a₁₉ = a₁₈ = a₁₇ = a₁₆ = a₁₅ = a₁₄ = a₁₃ = a₁₂ = a₁₁ =

= a₁₀ = a ₉= a ₈= a ₇ = a₆ = a₅ = a₄ = a₃ = a₂ = a₁ =0

Аналогично записываются условия для поверхностей, вытяну­тых вдоль двух других осей.

В общем виде уравнение поверхности, вытянутой вдоль оси ОХ, имеет вид

a₃₄x⁴+a₁₉x³+a₉x²+a₃x+a₆y²+a₄z²+a₀=0

Для получения сечения окружности необходимо выполнить дополнительное условие a6 = a4.

Для получения ограниченной поверхности коэффициенты a34, a6 и a4 должны иметь одинаковый знак.

На рис. 17.9 приведен пример такой поверхности — периформа. заданная уравнением x4+x3+y2+z2=0.

Для образования цилиндрической поверхности с осью, параллельной оси OZ, необходимо выполнение следующего условия:

_{a32 = a30 = a29 = a27 = a26 = a25 = a23 = a22 = a21 = a20 = a17 = a15 = a14 = a12 = a11 =}

_{= a}1_{0 = a 7 = a5 = a4 = a}3 _{= a}2 _{= a}1 ₌₀

Аналогично записываются условия для поверхностей с осями, параллельными двум другим осям.

В общем виде уравнение цилиндрической поверхности с осыо, параллельной оси OZ. имеет вид

a₃₄x⁴+a₃₃x³y+a₃₁x²y²+a₂₈xy³+a₂₄y⁴+a₁₉x³+a₁₈x²y+a₁₆xy²+a₁₃y³+a₉x²+a₈ x y+a₆y2+a₃x+a₂y+a₀=0.

Рис. 17.9 Рис. 17.10

На рис. 17.10 показана цилиндрическая поверхность с осью, параллельной оси OZ, и сложным постоянным сечением.

Метол конструирования симметричных поверхностей позволя­ет получить геометрические формы сравнительно узкого диапа­зона, однако эти формы часто встречаются в технике. Цилиндрические поверхности сложного профиля похожи на трубы сложного профиля, а периформа — на каплю жидкости. В свете изложенного создание библиотек типов и подтипов этих поверхностей является достаточно перспективным.

На рис. 17.11 —17.13 показаны некоторые поверхности 4-го по­рядка, которые можно включить в библиотеки и использовать для формирования более сложных объектов на основе технологии объединения поверхностей и описания их комбинации одним ал­гебраическим уравнением. В отдельных случаях обработка тако­го уравнения более эффективна, чем обработка системы несколь­ких уравнений.

Конструирование сложных поверхностей посредством объединения отдельных поверхностей. Довольно часто возни­кает задача создания геометрической формы, включающей в себя две более простые геометрические формы. При этом исходные формы могут пересекаться, не пересекаться, касаться или быть вложены друг в друга.

Рис. 17.11

Поверхности 3-го порядка могут образовываться объединением:

• трех плоскостей;

• плоскости и поверхности 2-го порядка.

• Поверхность 4-го порядка может образовываться объединением:

• четырех плоскостей;

• двух плоскостей и поверхности 2-го порядка;

• двух поверхностей 2-го порядка;

• поверхности 3-го порядка и плоскости.

Метод объединения поверхностей заключается в получении нового подтипа поверхностей посредством перемножения урав­нений, задающих поверхности более низкого порядка. При этом в качестве исходных могут выступать типы, подтипы и виды по­верхностей.

Пусть заданы две исходные поверхности f(x, у, z)=0 и g(x, у, z)=0.

Перемножив уравнения f(х, у, z) и g(x, у, z), получим новое уравнение h(x, у, z), степень которого равна сумме степеней ис­ходных уравнений.

Этот метод позволяет строить новые поверхности по уже из­вестным поверхностям. Так как при этом исходные поверхности могут иметь различные конфигурацию, размеры, расположение и ориентацию в любой точке пространства, то данный метод обеспечивает получение большого числа разнообразных форм (типов и подтипов) поверхностей. Например, поверхность, состоящая из двух цилиндрических поверхностей, может содержать пересекающиеся соосные, непересекающиеся соосные; вложен­ные, пересекающиеся несоосные и непересекающиеся несоосные цилиндры.

Представляется целесообразным разделять полученные объек­ты 4-го порядка на объекты, полученные объединением соосных поверхностей 2-го порядка и несоосных. Например, при объеди­нении двух цилиндров их оси могут быть совпадающими, парал­лельными. пересекающимися и скрещивающимися прямыми.

В случае объединения цилиндров с совпадающими и парал­лельными осями формула результирующей поверхности сохраня­ется относительно простой при удачном выборе осей координат (иными словами, существует вид такой поверхности, имеющей простую формулу). Также при угле 90° между осями объединен­ных цилиндров формула результирующей поверхности остается простой с небольшим числом радикалов. Однако при произволь­ном угле пересечения их осей невозможно выбрать систему коор­динат, обеспечивающую представление объединяемой геометри­ческой формы простой формулой, т. е. в этом случае все виды по­верхности задаются достаточно сложной формулой с большим числом радикалов.

Достоинством данного метода конструирования поверхностей является формирование сложной поверхности из известных гео­метрически понятных поверхностей.

Рис. 17.13

Рис. 17.14

Например, возьмем значения коэффициентов уравнений двух параболических цилиндров из программы формирования поверх­ностей (т.е. библиотечную поверхность), один из которых развер­нут на 180° по отношению к другому. Перемножив эта уравнения, получим уравнение цилиндра со сложным внутренним сечением (рис. 17.14):

x4 +у4 + 2х2y2 + 4х3 + 4xy2 - 2у2 – 2x2 - 8x = 0.

Полученные таким образом поверхности можно модифициро­вать, изменяя значения коэффициентов уравнения. Практиче­ское число таких поверхностей огромно.

Математическая обработка алгебраических уравнений поверх­ностей позволяет решать многие инженерные задачи с высокой точностью.