2.4. Алгоритмы сжатия аудиосигналов

2.4.1. Дифференциальная импульсно-кодовая модуляция

В обычной импульсно-кодовой модуляции каждый отсчет кодируется независимо от других. Однако у многих источников сигнала при стробировании с частотой Найквиста или быстрее проявляется значительная корреляция между последовательными отсчетами [5] (в частности, источник РС является квазистационарным источником и может относиться к рассматриваемым видам источников). Другими словами, изменение амплитуды между последовательными отсчетами в среднем относительно малы. Следовательно, схема кодирования, которая учитывает избыточность отсчетов, будет требовать более низкой битовой скорости.

При дифференциальной импульсно-кодовой модуляции (ДИКМ) по каналу связи передаются не значения отсчетов сообщения, а разность между отсчетами. Один из распространённых способов эффективной передачи непрерывных сообщений - способ передачи с предсказанием.

Последовательность коррелированных отсчётов исходного сигнала подают на один из входов вычитающего устройства, на другой вход поступает сигнал предсказания, сформированный из предыдущих отсчётов. Полученный сигнал ошибки предсказания поступает в тракт передачи. Поскольку в сигнале ошибки как раз и содержатся новые сведения, представляющие разность между истинным и предсказанным значением, то такой способ передачи называется передачей с предсказанием [5].

Известно большое число вариантов реализации кодирования с предсказанием. Основное различие сводится к различию операций формирования сигнала ошибки: в одних системах сигнал ошибки формируется в аналоговой форме, а затем кодируется, в других - вначале кодируется исходный аналоговый сигнал, а затем формируется сигнал ошибки.

В системах с ДИКМ обычно применяют неравномерное квантование сигнала ошибки, так как наиболее вероятны малые ошибки. Поскольку мощность шума квантования составляет определённую долю мощности квантуемого процесса, а мощность ошибки предсказания существенно меньше мощности сообщения, шум квантования при ДИКМ меньше, чем при обычной ИКМ при том же числе уровней. ДИКМ обеспечивает одинаковое с ИКМ качество передачи при меньшем числе символов в кодовой комбинации Корреляция между отсчётами возрастает по мере сокращения интервала между ними. Поэтому в пределе при большой частоте дискретизации число уровней квантования сигнала ошибки можно уменьшить до двух и перейти к одноразрядным системам.

Такой способ кодирования называют дельта-модуляцией (ДМ). Дельта модуляция (ДМ), отличается от ДИКМ тем, что передается только знак сигнала ошибки.

Предположим, что означает текущий отсчет источника, и пустьобозначает предсказанное значение (оценку) для, определяемое как

. (2.11)

Таким образом, является взвешенной линейной комбинациейM отсчетов, а являются коэффициентами предсказания. Величинывыбираются так, чтобы минимизировать некоторую функцию ошибки междуи.

Величина ошибки определяется как:

(2.12)

Виды линейных предсказаний. Рассмотрим виды предсказания. «Линейное» предсказание означает, что является линейной функцией предыдущих отсчетов; при «нелинейном» предсказании – это нелинейная функция. Порядок предсказания определяется количеством используемых предыдущих отсчетов. То есть, предсказание нулевого и первого порядка является линейным, а второго и более высокого порядка - нелинейным. При линейном предсказании восстановить сигнал значительно проще, чем при нелинейном предсказании. Будем рассматривать только линейное предсказание.

Предсказание нулевого порядка. В этом случае для предсказания текущего отсчета используется только предыдущий отсчет РС, т.е.

=> (2.13

Предсказание первого порядка (линейная экстраполяция). В этом случае для предсказания текущего отсчета используется не только предыдущий отсчет, но и разница между предпоследним и последним отсчетами, которая суммируется к общему результату:

(2.14)

Реализация ДИКМ. Определив метод определения коэффициентов предсказания, рассмотрим блок-схему практической системы ДИКМ, показанную ниже (рис. 2.13).

Рис 2.13. Блок-схема кодера ДИКМ

В этой схеме предсказатель стоит в цепи обратной связи, охватывающей квантователь. Вход предсказателя обозначен . Он представляет собой сигнальный отсчет , искаженный в результате квантования сигнала ошибки. Выход предсказателя равен:

; (2.15)

Разность является входом квантователя, аобозначает его выход. Величина квантованной ошибки предсказаниякодируется последовательностью двоичных символов и передается через канал в пункт приема. Квантованная ошибкатакже суммируется с предсказанной величиной, чтобы получить.

В месте приема используется такой же предсказатель, как на передаче, а его выход суммируется с, чтобы получить(см. рис. 2.14).

Рис.2.14. Блок-схема декодера ДИКМ

Сигнал является входным воздействием для предсказателя и в то же время образует входную последовательность, по которой с помощь ЦАП восстанавливается сигналx(t). Использование обратной связи вокруг квантователя обеспечивает то, что ошибка в - просто ошибка квантованияи что здесь нет накопления предыдущих ошибок квантования при декодировании. Имеем

(2.16)

Следовательно, . Это означает, что квантованный отсчетотличается от входаошибкой квантованиянезависимо от использования предсказателя. Значит, ошибки квантования не накапливаются.

В рассмотренной выше системе ДИКМ оценка или предсказанная величина отсчета сигналаполучается посредством линейной комбинации предыдущих значений,k = 1, 2, …, M, как показано в формуле (2.15). Улучшение качества оценки можно получить включением в оценку линейно отфильтрованных последних значений квантованной ошибки.

Конкретно, оценку можно выразить так:

,

где {} – коэффициенты фильтра для квантованной последовательности ошибок . Блок-схемы кодера на передаче и декодера на приеме приведены ниже на рис. 2.15.

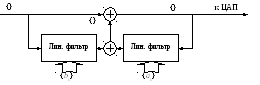
Рис.2.15. Блок-схема кодера и декодера ДИКМ с линейным фильтром

Здесь два ряда коэффициентов {} и {} выбираются так, чтобы минимизировать некоторую функцию ошибки , например, среднеквадратическую ошибку.

Наряду с равномерным (линейным) квантованием, при котором шаг квантования постоянен в пределах всего динамического диапазона, существует возможность согласования величины шага квантования с амплитудой сигнала. Для малых сигналов величина шага квантования мала, а для больших – возрастает. При этом с ростом амплитуды сигнала возрастает и мощность шумов квантования. Если использовать логарифмическую зависимость между выходным и входным сигналами, то можно поддерживать соотношение сигнал/шум квантования ниже заданной границы, как для малых, так и для больших по уровню сигналов (рис 2.16).

Рис. 2.16. Кусочно-линейная аппроксимация при адаптивном квантовании.

При использовании такого метода используется больше бит для слабых сигналов, где шум квантования наиболее заметен. Широко распространенный формат, использующий мю-функцию (), часто характеризуют как формат, сжимающий 12-битные отсчеты в 8-битные.

Адаптивная дифференциальная импульсно-кодовая модуляция. Многие реальные источники (например, источники РС), как уже было сказано выше, являются квазистационарными по своей природе. Одно из свойств квазистационарности характеристик случайного выхода источника заключается в том, что его дисперсия и автокорреляционная функция медленно меняются со временем. Кодеры ИКМ и ДИКМ, однако, проектируются в предположении, что выход источника стационарен. Эффективность и рабочие характеристики таких кодеров могут быть улучшены, если они будут адаптироваться к медленно меняющейся во времени статистике источника [5]. Как в ИКМ, так и в ДИКМ ошибка квантования , возникающая в равномерном квантователе, работающем с квазистационарным входным сигналом, будет иметь меняющуюся во времени дисперсию (мощность шума квантования).

Одно улучшение, которое уменьшает динамический диапазон шума квантования, - это использование адаптивного квантователя. Другое – сделать адаптивным предсказатель в ДИКМ. При этом коэффициенты предсказателя могут время от времени меняться, чтобы отразить меняющуюся статистику источника сигнала. Определенные таким образом коэффициенты предсказателя могут быть вместе с ошибкой квантования переданы приемнику, который использует такой же предсказатель. К сожалению, передача коэффициентов предсказателя приводит к увеличению необходимой битовой скорости, частично компенсируя снижение скорости, достигнутое посредством квантователя с немногими битами (немногими уровнями квантования) для уменьшения динамического диапазона ошибки, получаемой при адаптивном предсказании.

В качестве альтернативы предсказатель приемника может вычислить свои собственные коэффициенты предсказания через и, где

; (2.17)

Если пренебречь шумом квантования, эквивалентно. Следовательно,можно использовать для оценки АКФ в приемнике.

Основное преимущество такого метода адаптации – это отказ от решения СЛАУ, что значительно уменьшает вычислительные затраты.