
Надежность информационных систем2 / экзамен / NIS_5_laba
.docx|
Санкт-Петербургский Национальный Исследовательский Университет Информационных Технологий, Механики и Оптики |
|
Надежность информационных систем |
|
Лабораторная работа №5 Надежность программных и программно-аппаратных комплексов |
|
|
|
Работу выполнил: Дрожевский Александр |
|
Группа 5511 |
|
|
|
Преподаватель: Гусарова Н.Ф. |
|
Санкт-Петербург 2012 |
Задание
-
Выбрать программный или программно-аппаратный комплекс.
-
Выбрать две методики оценки надежности программного или программно-аппаратного комплекса. Методику необходимо выбирать таким образом, чтобы оценка показателей надежности осуществлялась по пяти метрикам.
-
Дать содержательное сравнительное описание получившихся результатов с точки зрения надежности комплекса и пригодности к тем или иным вариантам использования.
-
Необходимо показать, что выбранного объема кода достаточно для адекватного применения методики.
Основные показатели надежности программного обеспечения (ПО)
Надежность программного обеспечения отличается от надежности технических средств следующим
-
элементы ПО не стареют от износа
-
число способов контроля ПО значительно больше числа способов контроля аппаратуры
-
в ПО значительно больше объектов для контроля, чем в аппаратуре
-
в ПО гораздо проще вносить исправления и дополнения, чем в аппаратуру, но это трудно делать корректно и безошибочно.
Основные понятия, связанные с надежностью программного обеспечения:
-
ошибки в программах и признаки их наличия;
-
количество оставшихся в программе ошибок (ошибок, дошедших до пользователя); вероятность безотказной работы программы;
-
интенсивность обнаружения ошибок (или функция риска);
-
прогон программы;
-
отказ программы.
Дать строгое определение программной ошибки непросто, поскольку это определение, является функцией от самой программы, то есть зависит от того, какого функционирования ожидает от программы пользователь. По этой причине вместо строгого определения будут перечислены только признаки, указывающие на наличие ошибки в программе:
-
при выполнении программы появилась ошибочная операция
-
использование некорректного операнда в программе;
-
несоответствие функций, выполняемых программой, ее спецификации;
-
ошибки в самой спецификации, которые вызывают необходимость корректирования программы;
-
ошибки в вычислениях (например, переполнение и т.п.);
-
ошибки интерфейса программы с пользователем.
Этот список можно считать открытым, поскольку он может быть продолжен разработчиками по мере накопления ими опыта в повышении надежности программного обеспечения.
Все же чаще всего под ошибкой (или отказом) программы понимают всякое невыполнение программой функций, которые были предусмотрены в техническом задании на ее разработку или вытекают непосредственно из инструкций пользователю. Является некорректным относить к ошибкам, например, необходимость написания программного кода, заменяющего какую-либо временно отсутствующую часть программы, или же необходимость рекомпиляции, вызванную изменениями в других модулях.
Количество оставшихся в программе ошибок – это количество ошибок, которые потенциально могут быть обнаружены на последующих стадиях жизненного цикла программы, после исправлений, внесенных в программу на текущей стадии ее жизненного цикла. Это количество оставшихся в программе ошибок (обозначаемое далее как B) – один из важнейших показателей надежности ПО.
Пусть P(t) - вероятность того, что ни одной ошибки не будет обнаружено на временном интервале [0,t]. Тогда вероятность хотя бы одного отказа за этот период будет Q(t) = 1 – P(t), и плотность вероятности можно записать как

Рассмотрим функцию риска R(t), как условную плотность вероятности отказа программы в момент времени t, при условии, что до этого момента отказов не было
 (1)
(1)
Функция риска имеет размерность [1/время] и она очень полезна при классификации основных распределений отказов. Распределения с возрастающей функцией риска соответствуют тем ситуациям, когда статистические характеристики надежности ухудшаются со временем. И наоборот, распределения с убывающей функцией риска соответствуют обратной ситуации, когда надежность улучшается со временем в результате процесса обнаружения и коррекции ошибок.
Из выражения (13.1), ясно, что
 ,
и, следовательно,
,
и, следовательно,

или
 (2)
(2)
Равенство (2) является одним из самых важных в теории надежности. В дальнейшем будет показано, что различные виды поведения функции риска во времени порождают различные возможности для построения моделей надежности ПО. Интенсивность обнаружения ошибок (функция риска), вместе с вероятностью безотказной работы программы и количеством оставшихся в программе ошибок, являются важнейшими показателями надежности программ.
Прогон программы – это набор
действий, включающий в себя: ввод в
программу одной из возможных комбинаций
Ei пространства входных данных E
( );
выполнение программы, которое заканчивается
либо получением результата F(Ei),
либо отказом.
);
выполнение программы, которое заканчивается
либо получением результата F(Ei),
либо отказом.
Для некоторых наборов входных данных
Ei, отклонение полученного на
выходе результата (F’(Ei)) от
требуемого результата F(Ei) находится
в пределах допустимого отклонения
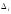 ,
то есть выполняется следующее неравенство
,
то есть выполняется следующее неравенство
 (3)
(3)
а для всех остальных Ei из
подмножества
 ,
выполнение программы не дает приемлемого
результата, то есть
,
выполнение программы не дает приемлемого
результата, то есть
 (4)
(4)
Случаи, описанные неравенством (4), называются отказами программы.
Рассмотрим дихотомическую переменную
 :
:

Тогда статистическая оценка вероятности отказа программы в течении m прогонов будет равна:
 (5)
(5)
Обозначим через
 приемлемую ошибку оценки
приемлемую ошибку оценки
 вероятности отказа
вероятности отказа
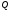 .
Тогда требуемое количество прогонов
программы m должно быть пропорционально
значению
.
Тогда требуемое количество прогонов
программы m должно быть пропорционально
значению
 ,
где Q – заданная вероятность отказа
программы. Это означает, что если,
например, требуемая относительная
ошибка оценки (5)
,
где Q – заданная вероятность отказа
программы. Это означает, что если,
например, требуемая относительная
ошибка оценки (5)
 ,
и требуемое (желаемое) значение
,
и требуемое (желаемое) значение
 ,
тогда количество независимых прогонов
программы m одлжно быть не меньше, чем
,
тогда количество независимых прогонов
программы m одлжно быть не меньше, чем
 ,
что, конечно, нелегко реализовать на
практике. Решением этой проблемы может
быть использование процедуры
последовательного анализа Вальда.
,
что, конечно, нелегко реализовать на
практике. Решением этой проблемы может
быть использование процедуры
последовательного анализа Вальда.
И наконец, еще один показатель надежности ПО, который тоже будет использоваться в этой работе – среднее время наработки программы до отказа:

Опыт разработки ПО показывает, что выявление ошибок и их исправление связано с определенными затратами, которые составляют цену ошибки. По мере перехода к более поздним стадиям разработки цена ошибки возрастает
-
Этап разработки спецификаций 140$;
-
Программирование 1100$;
-
Комплексная отладка 7000$
-
Этап сопровождения от 14000$ до 140 000$
Процентные частоты появления ошибок в ПО по типам ошибок представлены в таблице:
|
ТИП ОШИБКИ |
ЧАСТОТА ПОЯВЛЕНИЯ, % |
|
Не полная или ошибочная спецификация |
28 |
|
Отклонение от спецификации |
12 |
|
Пренебрежение правилами программирования |
10 |
|
Ошибочная выборка данных |
10 |
|
Ошибочная логика или последовательность операций |
12 |
|
Ошибочные арифметические операции |
9 |
|
Нехватка времени для решения |
4 |
|
Ошибка обработки прерываний |
4 |
|
Ошибка в исходных данных |
3 |
|
Неточная запись |
8 |
Выбор программного комплекса
Для оценки была выбрана корпоративная информационная система для автоматизации работы небольшого производства мебели. В системе предусмотрено два варианта работы: автоматический – имитационно модулируются заказы (рис.1) и ручной – менеджер front-office заносит заказы в систему с некоторой периодичностью (рис.2).

Рис.1 - Имитационное моделирование

Рис.2 - Front Office
Метод Джелинского-Моранды
Это одна из первых и простейших моделей классического типа, послужившая основой для дальнейших разработок в этом направлении. Модель была использована при разработке таких значительных программных проектов, как программа Аполло (некоторых ее модулей). Модель Джелинского-Моранды основана на следующих предположениях:
-
Интенсивность обнаружения ошибок R(t) пропорциональна текущему количеству ошибок в программе, то есть изначальному количеству ошибок за вычетом количества ошибок, уже обнаруженных на данный момент.
-
Все ошибки в программе равновероятны и не зависят друг от друга.
-
Все ошибки имеют одинаковую степень важности.
-
Время до следующего отказа программы распределено экспоненциально.
-
Исправление ошибок происходит без внесения в программу новых ошибок.
-
R(t) = const в промежутке между любыми двумя соседними моментами обнаружения ошибок.
Согласно этим предположениям, функция риска будет представлена как:

В этой формуле t – это произвольный момент времени между обнаружением (i-1)-й и i-й ошибок; K – неизвестный коэффициент масштабирования; B – начальное количество оставшихся в программе ошибок (также неизвестное). Таким образом, если в течении времени t было обнаружено (i-1) ошибок, это означает, что в программе еще остается B-(i-1) необнаруженных ошибок. Полагая, что

и используя предпосылку 6, а также равенство (2), можно заключить, что все Xi имеют экспоненциальное распределение

и плотность вероятности отказа,
соответственно, равна

Тогда функцию правдоподобия (согласно предпосылке 2) можно записать как


или, переходя к логарифму функции правдоподобия, имеем
 (2)
(2)
Максимум функции правдоподобия можно найти, используя следующие условия
 (3)
(3)
 (4)
(4)
Из формулы (3) получается оценка максимального правдоподобия для K
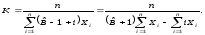 (5)
(5)
Подставляя выражение (5) в (4), находим
нелинейное уравнение для вычисления
 –оценки максимального правдоподобия
для B
–оценки максимального правдоподобия
для B
 (6)
(6)
Это уравнение можно упростить перед тем, как искать его решение, если записать его с использованием следующих обозначений
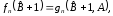 (7)
(7)
где

Поскольку имеют смысл лишь целочисленные
значения
 ,
функции из выражения (7) можно рассматривать
только для целочисленных аргументов.
Более того,
,
функции из выражения (7) можно рассматривать
только для целочисленных аргументов.
Более того,
 ,
поскольку n ошибок с программе уже
обнаружено. Таким образом, оценка
максимального правдоподобия для B может
быть получена с помощью вычисления
начальных значений функций fn(m) и
gn(m) для m=n+1, n+2…, и анализа разницы
|fn(m)-gn(m)|.
,
поскольку n ошибок с программе уже
обнаружено. Таким образом, оценка
максимального правдоподобия для B может
быть получена с помощью вычисления
начальных значений функций fn(m) и
gn(m) для m=n+1, n+2…, и анализа разницы
|fn(m)-gn(m)|.
Поскольку правая и левая части выражения
(7) одинаково монотонны, это порождает
проблему единственности решения, а
также проблему его существования.
Конечное решение
 в области
в области
 существует тогда и только тогда, когда
выполняется неравенство
существует тогда и только тогда, когда
выполняется неравенство
 (8)
(8)
В противном случае оценка максимального
правдоподобия будет
 Условие
(8) можно переписать в более удобном виде
Условие
(8) можно переписать в более удобном виде
 (9)
(9)
где A – то же самое выражение, что и в формуле (7). Необходимо отметить, что, A является интегральной характеристикой n встретившихся в программе за время тестирования ошибок, и представляет (в статистическом смысле) набор интервалов Xi между ошибками.
Оценка надежности КИС методом Джелинского-Моранды
Экспериментальные данные: в течение 240 минут было обнаружено 8 ошибок, интервалы между обнаружением которых представлены в таблице.
|
i
|
Xi |
|
1 |
9 |
|
2 |
38 |
|
3 |
52 |
|
4 |
16 |
|
5 |
27 |
|
6 |
29 |
|
7 |
5 |
|
8 |
64 |
Для этих данных мы имеем n=8 и
 Условие
Условие
 выполняется, и, таким образом, оценка
максимального правдоподобия имеет
единственное решение. В таблице
представлены начальные значения функций
для множества аргументов
выполняется, и, таким образом, оценка
максимального правдоподобия имеет
единственное решение. В таблице
представлены начальные значения функций
для множества аргументов

|
m |
|
|
|
|
9 |
2,717857 |
1,921922 |
0,795935 |
|
10 |
1,828968 |
1,549637 |
0,279331 |
|
11 |
1,428968 |
1,298174 |
0,130794 |
|
12 |
1,186544 |
1,116928 |
0,069616 |
|
13 |
1,019877 |
0,980092 |
0,039785 |
|
14 |
0,8968 |
0,873124 |
0,023676 |
|
15 |
0,801562 |
0,787208 |
0,014354 |
|
16 |
0,725372 |
0,716685 |
0,008687 |
|
17 |
0,662872 |
0,65776 |
0,005112 |
|
18 |
0,610584 |
0,607787 |
0,002797 |
|
19 |
0,56614 |
0,564872 |
0,001268 |
|
20 |
0,527862 |
0,527617 |
0,000245 |
|
21 |
0,494529 |
0,494973 |
-0,00044 |
|
22 |
0,465225 |
0,466133 |
-0,00091 |
Наилучшим решением для уравнения
является m=20 (соответствующая строка в
таблице дает минимальное значение
разницы функций по модулю, то есть
максимально приближает ее к нулю, что
нам и требуется), то есть
 =
m-1=19.
=
m-1=19.

Среднее время
 (время, оставшееся до обнаружения (n+1)-й
ошибки) есть инвертированная оценка
интенсивности для предыдущей ошибки:
(время, оставшееся до обнаружения (n+1)-й
ошибки) есть инвертированная оценка
интенсивности для предыдущей ошибки:



 ,
и время до полного завершения тестирования:
,
и время до полного завершения тестирования:
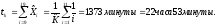
Плотность вероятности отказов равна:

|
i
|
Xi |
q(Xi) |
|
1 |
9 |
0,0287 |
|
2 |
38 |
0,0088 |
|
3 |
52 |
0,0053 |
|
4 |
16 |
0,0200 |
|
5 |
27 |
0,0135 |
|
6 |
29 |
0,0126 |
|
7 |
5 |
0,0248 |
|
8 |
64 |
0,0049 |
Модель Липова
Липов модифицировал модель Миллса, рассмотрев вероятность обнаружения ошибки при использовании различного числа тестов. Если сделать то же предположение, что и модель Миллса, т.е. что собственные и искусственные ошибки имеют равную вероятность быть найденными, то вероятность обнаружения n собственных и V внесенных ошибок равна:
 где m –
количество тестов, используемых при
тестировании;
где m –
количество тестов, используемых при
тестировании;
q - вероятность обнаружения ошибки в каждом из m тестов, рассчитывается по формуле:
 S
– общее количество искусственно
внесенных ошибок;
S
– общее количество искусственно
внесенных ошибок;
N – количество собственных ошибок, имеюшихся в ПО до начала тестирования.

Для использования модели Липова должны выполняться следующие условия:
 Модель
Липова дополняет модель Миллса, дав
возможность оценить вероятность
обнаружения определенного количества
ошибок к моменту оценки.
Модель
Липова дополняет модель Миллса, дав
возможность оценить вероятность
обнаружения определенного количества
ошибок к моменту оценки.
Оценка надежности КИС методом Липова
Экспериментальные данные:
-
общее количество искусственно внесенных ошибок S = 20;
-
количество тестов, используемых при тестировании m = 70;
-
количество найденных собственных ошибок n = 8;
-
количество найденных внесенных ошибок V = 12.
Тогда предполагаемое количество собственных ошибок, имеющихся в ПО до начала тестирования:

А вероятность обнаружения ошибки в каждом из 70 тестов:

Вероятность обнаружения n собственных и V внесенных ошибок равна:




