
Моделирование / Расчет сопротивления
.pdf
33
Бондаров Михаил Николаевич
Учитель физики лицея №1501 и ГОУ ЦО «Технологии обучения» г. Москвы.
Расч¸т сопротивления электрической цепи
В статье на примерах решения конкретных задач показано применение различных способов расч¸та сопротивления электриче- ской цепи. Рассмотрены некоторые методы преобразования электрических схем к эквивалентным схемам.
Введение
Задачи на расч¸т сопротивления электрической цепи можно встретить среди экзаменационных и олимпиадных задач, а также в заданиях ЕГЭ. В данной статье мы рас-
смотрим некоторые при¸мы, позволяющие достаточно эффективно определять сопротивления различных цепей. Напомним основные закономерности.
1. Последовательное и параллельное соединения проводников
В электрических цепях, с которыми можно встретиться на практике, проводники соединяются различными способами. Наиболее простые соединения известны как последовательное и параллельное соединения.
При последовательном соединении один проводник следует за другим так, что конец одного служит началом другого (рис. 1). Обратите внимание, что при этом между проводниками нет разветвлений проводов.
Из курса физики 8 класса известно, что общее сопротивление R последовательно соедин¸нных про-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
à |
|
á |
|
|
|
â |
|
|
||||||||
|
|
|
|
|
Ðèñ. 1 |
|
|
|
|
|
|
|
|
|||
водников сопротивлениями R1 è R2 |
||||||||||||||||
определяется по формуле: |
|
|
|
|
|
|||||||||||
|
|
|
|
R |
R1 R2. |
|
|
|
|
|
||||||
При параллельном соединении проводники подключаются к одной и той же паре точек А и В (рис. 2).
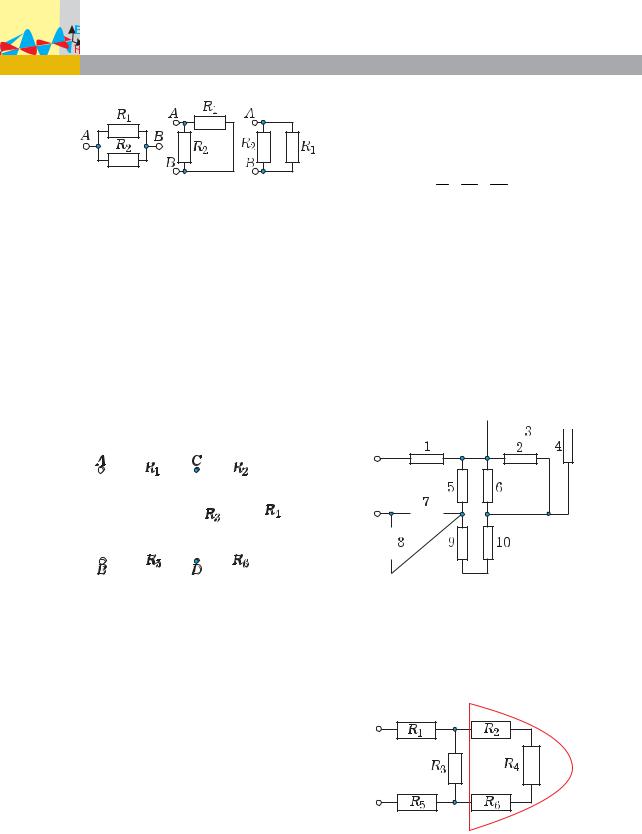
34 Физика
|
|
Общее сопротивление R парал- |
||||
|
|
лельно |
соедин¸нных |
проводников |
||
|
|
сопротивлениями R1 è R2 опреде- |
||||
|
|
ляется из соотношения: |
|
|||
à |
á |
â |
1 |
1 |
1 . |
|
|
Ðèñ. 2 |
|
R |
R1 |
R2 |
|
|
|
|
|
|
|
|
2. Распознавание типов соединений
Для уверенного |
решения |
задач |
соединены последовательно, не за- |
|||||||||||
на определение общего сопротивле- |
мечая того, что узлы C и D между |
|||||||||||||
íèÿ |
электрической |
öåïè |
важно |
ними свидетельствуют о разветвле- |
||||||||||
уметь в сложных схемах распозна- |
нии проводов. |
|
|
|
|
|
|
|
|
|
|
|||
вать проводники, соедин¸нные по- |
Пример 2. |
Рассмотрим |
åù¸ |
|||||||||||
следовательно или параллельно. |
одну схему (рис. 4). Попробуйте |
|||||||||||||
Рассмотрим конкретные примеры. |
найти в ней последовательно и |
|||||||||||||
Пример 1. В схеме, изображ¸н- |
параллельно |
соедин¸нные |
|
ïðî- |
||||||||||
íîé |
на рис. 3, только проводники |
водники (свой ответ проверьте по |
||||||||||||
R2, |
R4 è R6 соединены последо- |
ðèñ. 28). |
|
|
|
|
|
|
|
|
|
|
||
вательно. Иногда |
ошибочно |
ñ÷è- |
|
|
|
|
|
|
|
|
|
|
|
|
тают, что все проводники, кроме R3, |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 3 |
Ðèñ. 4 |
|
|||||||||||||||||
3. Смешанное соединение проводников
Приступим теперь к расч¸ту сопротивления при смешанном соединении проводников. Начн¸м с простых цепей.
Задача 1. Определите общее сопротивление цепи, схема которой изображена на рис. 3, если все проводники имеют сопротивление по 4 Ом.
Решение. Учитывая анализ, провед¸нный в примере 1, выделим три последовательно соедин¸нных проводника R2, R4 è R6 (ðèñ. 5).
На эквивалентной схеме (рис. 6) их можно заменить одним проводником сопротивлением
R246 R2 R4 R6 12 Îì.
Теперь ясно видно, что проводник сопротивлением R246 соедин¸н
Ðèñ. 5
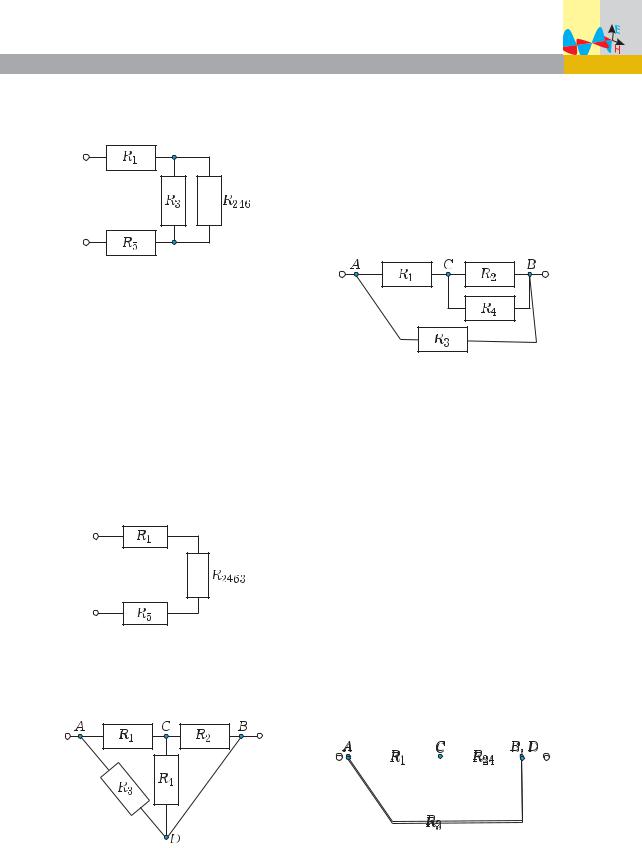
параллельно с проводником сопротивлением R3 .
Ðèñ. 6
Определим их общее сопротивление R2463 :
1 |
|
|
1 |
|
1 |
|
|
||
|
|
|
|
|
|||||
|
R2463 |
|
|
R3 |
|
R246 |
|
||
R2463 |
|
R246 |
R3 |
|
3 Ом. |
||||
|
R246 |
R3 |
|||||||
|
|
|
|
||||||
На эквивалентной схеме (рис. 7) видно, что исчезли узлы между
проводниками R1, R2463 è R5 , поэтому эти проводники оказались соедин¸нными последовательно, и их общее сопротивление
R R1 R2463 R5 11 Îì.
Ðèñ. 7
Ответ: 11 Ом.
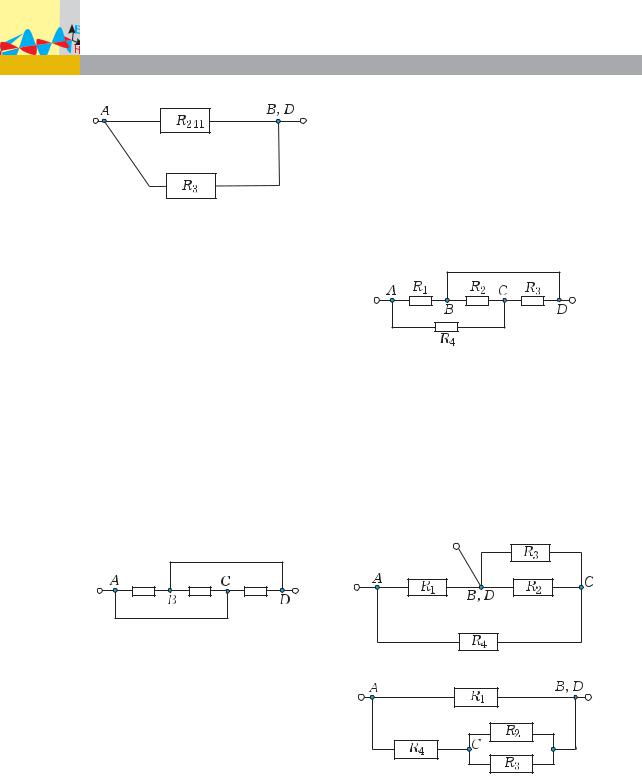
Задача 2. В цепи, схема которой изображена на рис. 8, все проводни-
Физика 35
ки имеют сопротивление по 10 Ом. Чему равно общее сопротивление цепи между точками А и В?
Решение. Обратите внимание, что точки В и D соединены проводом с нулевым сопротивлением, следовательно, их можно объединить в один узел. Тогда эквивалентная схема будет иметь вид, изобра- ж¸нный на рис. 9.
Ðèñ. 9
Теперь общее сопротивление цепи легко находится в три этапа.
1) Сначала вычисляем сопротивление параллельно соедин¸нных проводников R2 è R4 :
R24 |
R2 |
R4 |
5 |
Îì. |
|
R2 |
R4 |
||||
|
|
|
На преобразованной схеме вместо проводников R2 è R4 рисуем эквивалентный им проводник R24 (ðèñ. 10 a).
2) Затем определяем сопротивление последовательно соедин¸нных проводников R24 è R1:
R241 R24 R1 15 Îì.
На рис. 10 б показана новая эквивалентная схема.
3) Наконец, находим общее сопротивление цепи:
|
|
R |
R241 |
R3 |
6 |
Îì. |
|
|
|||
|
|
R241 |
R3 |
|
|
||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 10 à
Ðèñ. 8
36 Физика
Ðèñ. 10 á
Ответ: 6 Ом.
Заметим, что преобразуя цепь к более простой эквивалентной, можно на схемах изгибать, удлинять или укорачивать провода, перемещать узлы вдоль проводов, поскольку провода, соединяющие элементы схемы, считаются идеальными, т. е. имеющими нулевое сопротивление.
Рассмотрим теперь, как может видоизмениться цепь, состоящая из тр¸х последовательно соедин¸нных проводников, если к ним добавить другие проводники. Сначала добавим два проводника с нулевым сопротивлением, соединив ими точку А с точ- кой С, а В – с D (рис. 11).
Задача 3. Найдите сопротивление между точками А и D цепи (рис. 11), если каждый проводник имеет сопротивление 3 Ом.
Ðèñ. 11
Решение. Так как точки А и С соединены проводом с нулевым сопротивлением, то их потенциалы равны, а значит, эти точки имеют одинаковый потенциал, и их можно собрать в один общий узел. Аналогично поступим с точками В и D. Таким образом, полу- чилось, что каждый проводник оказался подключенным к одним и тем же точкам, т. е. все три проводника соединены параллельно. Теперь уже легко найти общее сопротивление цепи, учи- тывая, что все проводники имеют одинаковое сопротивление:
1 |
1 |
|
1 |
|
1 |
3 |
R |
R1 |
1 |
Îì. |
||
R |
|
R1 |
R1 |
R1 |
|
R1 |
3 |
|||||
|
|
|
|
|
|
|
||||||
Ответ: 1 Ом.
Заменим теперь один из идеальных проводников реальным – с ненулевым сопротивлением.
Задача 4. Определите сопротивление между точками А и D цепи (рис. 12), если каждый проводник имеет сопротивление 6 Ом.
Ðèñ. 12
Заметим, что точки В и D попрежнему соединены проводником с нулевым сопротивлением. Следовательно, они имеют одинаковый потенциал. Соединив их в один узел, получим эквивалентную схему (рис. 13 а). Если же затем «распрямить» е¸, то участки с параллельно и последовательно соедин¸н- ными проводниками станут хорошо видны (рис. 13 б).
Ðèñ. 13 à
Ðèñ. 13 á
После этого останется лишь произвести расч¸т сопротивления для эквивалентной схемы в три этапа:
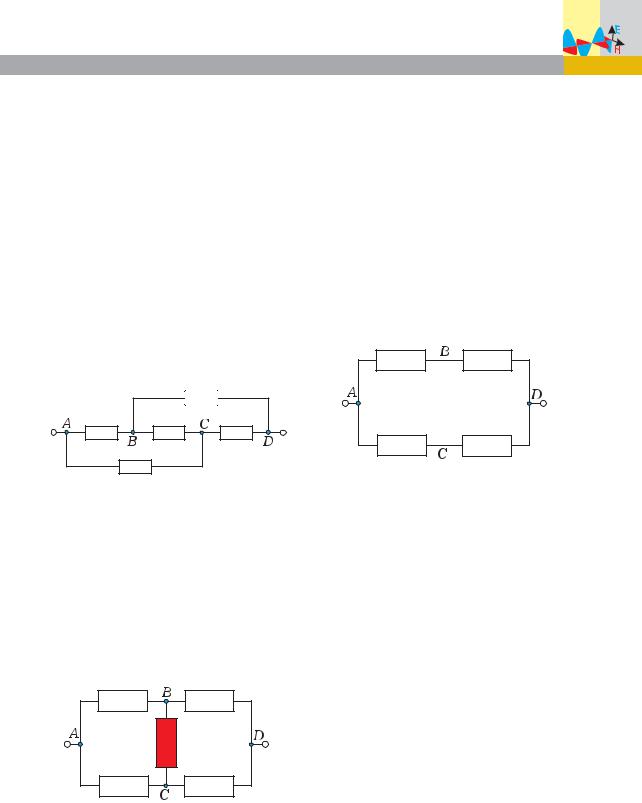
Физика 37
1) |
|
1 |
|
1 |
|
1 |
|
|
|
3) |
1 |
|
1 |
|
|
1 |
|
|
|
||||
|
R23 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
R2 |
|
R3 |
|
|
|
|
R R1 R234 |
|
|
||||||||||||
|
|
R23 |
|
|
R2 |
R3 |
3 |
Îì; |
|
R |
R1 |
R234 |
3,6 |
Îì. |
|||||||||
|
|
|
|
R2 |
R3 |
|
R1 |
R234 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2) |
R234 |
R4 |
R23 |
9 Îì; |
|
Ответ: 3,6 Ом. |
|
|
|
||||||||||||||
4. Мостиковая схема
Заменив второй идеальный проводник в цепи, схема которой показана на рис. 11, реальным, получим новую цепь, схема которой изображена на рис. 14.
Задача 5. Определите сопротивление между точками А и D цепи, схема которой изображена на рис. 14, если сопротивление каждого проводника равно 2 Ом.
Ðèñ. 14
Решение. На этот раз все попытки обнаружить хотя бы одну пару последовательно или параллельно соедин¸нных проводников оказываются безуспешными. И вс¸ же попробуем немного видоизменить схему так, чтобы можно было увидеть в ней элементы симметрии. Немного потренировавшись, можно получить следующую схему – она носит название «мостиковая схема» (рис. 15).
Ðèñ. 15
Поскольку все проводники имеют одинаковое сопротивление, то по
ветвям ABD и ACD текут одинаковые токи, а через выделенную красным цветом перемычку ВС ток идти не будет. Поэтому перемычку можно безболезненно удалить из цепи, не изменив при этом общее сопротивление цепи (рис. 16).
Ðèñ. 16
Заметим кстати, что ток через перемычку не будет идти при любом е¸ сопротивлении, если для остальных проводников выполняется соотношение:
RAB |
|
RBD |
. |
(*) |
|
|
|||
RAC |
|
RCD |
|
|
Теперь же ясно видно, что цепь состоит из двух параллельно соеди- н¸нных участков, в которых находится по два последовательно соеди- н¸нных проводника. Определим сна- чала сопротивление каждого из этих участков: RABD RAСD (2 2) Ом
4 Ом. Затем находим общее сопротивление цепи:
1 |
1 |
|
1 |
|
2 |
|
|||
|
|
RABD |
RACD |
|
|
|
|||
R |
|
|
|
|
RABD |
||||
|
|
R |
|
RABD |
2 Ом. |
||||
|
|
|
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
Ответ: 2 Ом.
Задача 6. Каково сопротивление
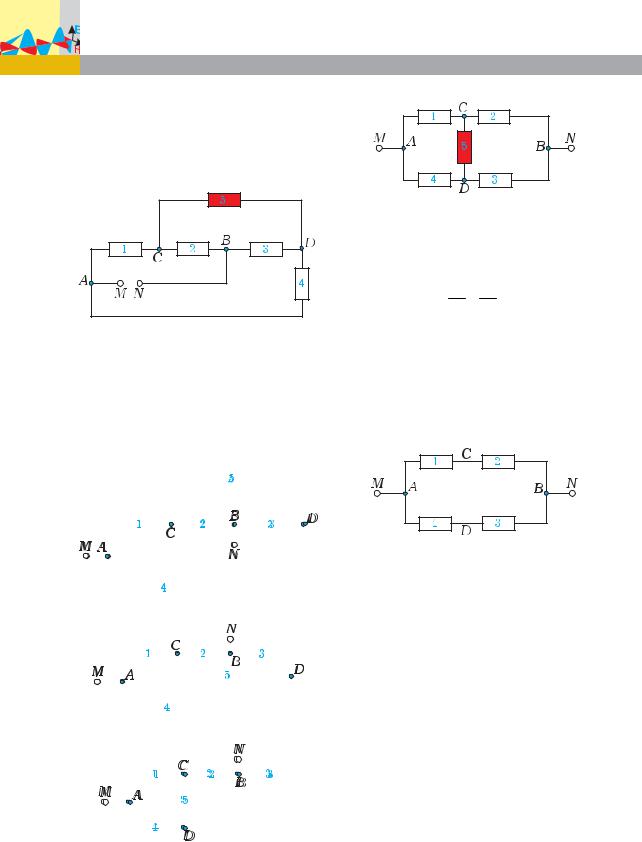
38 Физика
между точками N и M цепи, схема которой показана на рис. 17, если сопротивления проводников
R1 1 Ом, R2 2 Ом, R3 4 Ом, R4 2 Ом, R5 5 Ом?
Ðèñ. 17 |
Решение. В данном случае не очевидно, что ток через выделенный красным цветом проводник 5 идти не будет. И вс¸ же, проделав несколько манипуляций с цепью, можно полу- чить мостиковую схему (этапы преобразований показаны на рис. 18 a–г).
ã
Ðèñ. 18
Обратим внимание, что по условию задачи
R1 R2 ,
R4 R3
то есть выполняется соотношение (*). Следовательно, потенциалы точек С и D одинаковы, через проводник 5 ток не ид¸т, и его можно удалить, не изменяя сопротивление цепи. После этого эквивалентная схема выглядит совсем просто (рис. 18 д).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 18 ä |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Произвед¸м |
ðàñ÷¸ò |
сопротивле- |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
íèÿ öåïè: |
|
|
|
R2 |
3 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
à |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R12 |
R1 |
Îì; |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R43 |
R4 |
R3 |
6 Îì; |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
R |
R12 |
R43 |
2 Îì. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
R12 |
R43 |
R12 |
R43 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 2 Ом. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Заметим, что если все попытки |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
распутать и упростить схему из пя- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
á |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ти проводников не приводят к успе- |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ху, вполне вероятно, что вы натолк- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нулись на «мостиковую схему» (как, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
например, на рис. 17). |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При определении общего сопро- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тивления в задачах 5 и 6 мы ис- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
пользовали симметрию схемы. По- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
знакомимся более подробно с при¸- |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
â |
|
|
|
|
|
|
|
|
|
|
|
|
мами, позволяющими рассчитывать |
||||||||||||||||
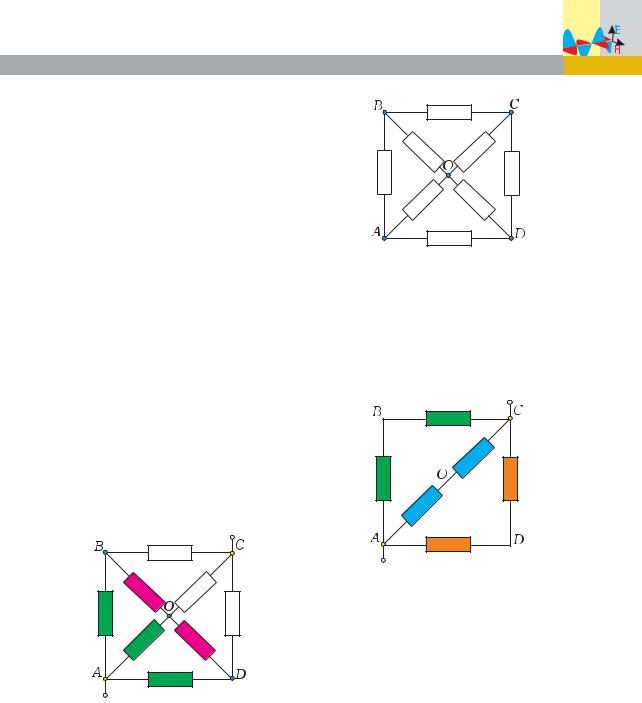
Физика 39
сопротивления подобных |
цепей. |
Для этого рассмотрим цепь, со- |
|
стоящую из одинаковых проводни- |
|
ков, включ¸нных в каждую из сто- |
|
рон квадрата. Кроме того, каждая |
|
из вершин соединена с центром |
|
квадрата такими же проводниками |
|
(ðèñ. 19). |
|
В зависимости от точек под- |
|
ключения цепи в ней проявляются |
|
различные виды симметрии. |
Ðèñ. 19 |
5. Метод исключения участков цепи
Задача 7. Определите сопротивление между точками А и С цепи (рис. 19), если каждый проводник имеет сопротивление 3 Ом.
Решение. Из симметрии схемы (рис. 20) следует, что по выделенным зел¸ным цветом проводникам будут идти одинаковые токи, следовательно, потенциалы точек В, О и D будут одинаковы. Тогда по проводникам, выделенным красным цветом, токи идти не будут, и их можно удалить из цепи, не изменив при этом е¸ общее сопротивление.
Ðèñ. 20
В результате схема упростится (рис. 21), выделенные одинаково проводники тр¸х ветвей окажутся соедин¸нными последовательно, а сами ветви соединены между собой параллельно.
Ðèñ. 21
Теперь уже дальнейший расч¸т несложен: сопротивление каждой ветви равно 6 Ом, а общее сопротивление цепи составляет 2 Ом.
Ответ: 2 Ом.
Заметим, что именно этот при¸м был использован при решении задач 5 и 6.
6. Метод разрезания узлов
Рассмотрим другое подключение цепи, схема которой показана на рис. 19.
Задача 8. Найдите сопротивление между точками А и D цепи (рис. 22), если каждый проводник имеет сопротивление 6 Ом.
Решение. Используем теперь
метод разрезания узлов. Для этого узел О разделим на два, получив при этом точки O1 è O2 с одинаковыми потенциалами (равными среднему арифметическому между потенциалами узлов А и D). Пронуме-
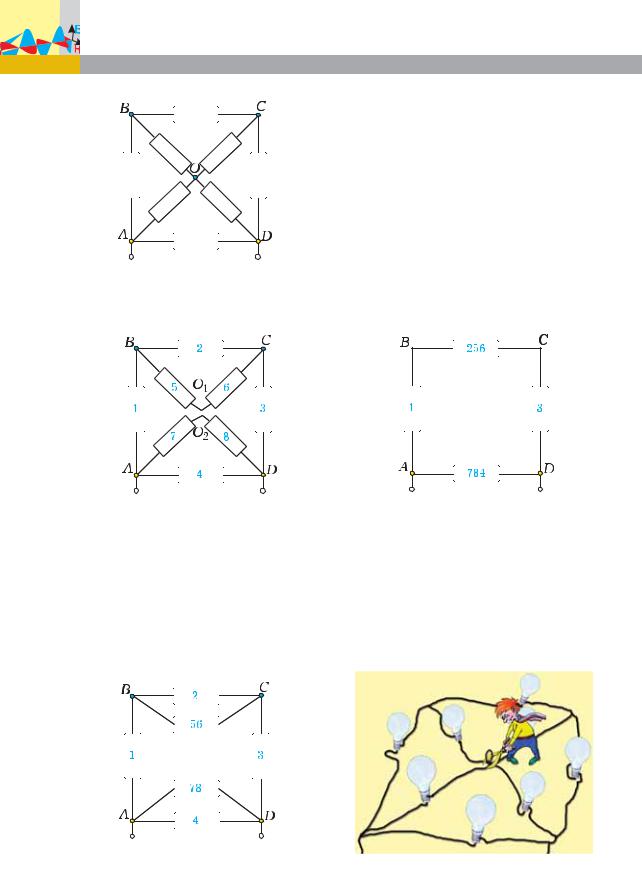
40 Физика
Ðèñ. 22
руем также проводники для удобства описания (рис. 23).
Ðèñ. 23
После разрезания узла О проводники 5 и 6 оказались соедин¸н- ными последовательно так же, как и проводники 7 и 8. Заменив их проводниками с эквивалентными сопротивлениями
R56 |
R5 R6 |
12 Îì è |
R78 |
R7 R8 |
12 Îì, |
получим более простую схему (рис. 24).
Ðèñ. 24
Заменим теперь параллельно соедин¸нные проводники 2 и 56 проводником с эквивалентным сопротивлением R256 :
1 |
|
|
1 |
|
1 |
|
||
|
|
|
|
|
||||
|
R256 |
|
|
R2 |
R56 |
|
||
R256 |
|
R2 R56 |
|
4 Ом. |
||||
|
R2 R56 |
|||||||
|
|
|
|
|||||
Поступим аналогично и с проводниками 78 и 4: эквивалентное сопротивление R784 также равно 4 Ом.
Теперь схема ещ¸ более упрощается (рис. 25).
Ðèñ. 25
Дальнейший расч¸т несложен:
R12563 |
R1 R256 R3 16 Îì; |
||||||||||
1 |
|
1 |
|
|
1 |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
R |
R12563 |
|
|
R784 |
|||||
R |
R12563 R784 |
|
|
|
16 4 |
3,2 Ом. |
|||||
R12563 R784 |
|
|
16 4 |
||||||||
|
|
|
|
||||||||
Ответ: 3,2 Ом.
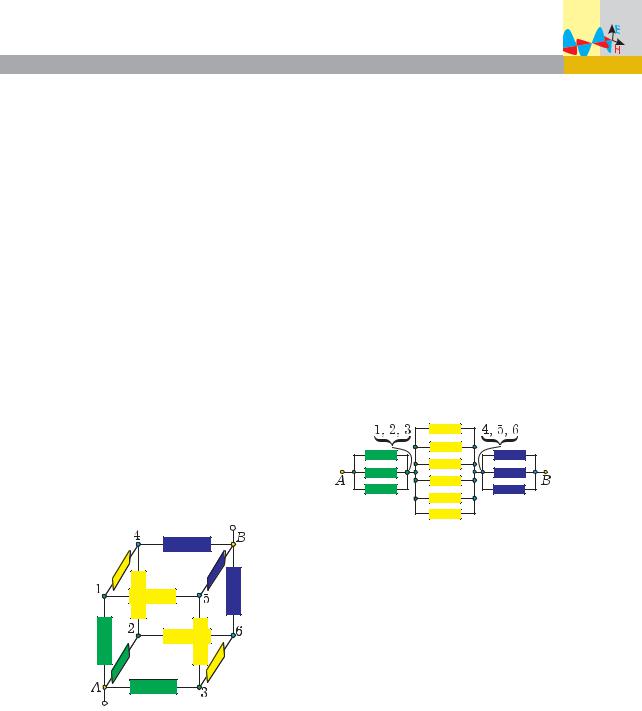
Физика 41
7. Метод склеивания узлов
Этот метод является обратным по отношению к предыдущему.
Задача 9. В каждое из р¸бер куба включ¸н проводник сопротивлением 6 Ом. Чему равно сопротивление получившейся конструкции между вершинами А и В, находящимися на концах большой диагонали куба?
Решение. Используем теперь метод склеивания узлов.
Изобразим на чертеже схему включения проводников (рис. 26). Учитывая симметрию схемы, заметим, что токи через проводники, выделенные зел¸ным, одинаковы. Следовательно, потенциалы точек 1, 2 и 3 равны. Тогда, если их соединить идеальными проводниками, то по этим проводникам ток идти не будет, а значит общее сопротивление цепи не изменится. Таким образом, точки 1, 2 и 3 оказались собранными в один узел, а выделенные зел¸ным проводники стали соедин¸нными параллельно.
Ðèñ. 26
Поступив аналогично с проводниками, выделенными синим, полу- чим три других параллельно соеди- н¸нных проводника.
Обратим внимание, что шесть оставшихся проводников (они выделены ж¸лтым цветом) теперь оказываются соедин¸нными параллельно. Действительно, каждый из них одним концом подключ¸н к узлу, выделенному зел¸ным цветом, а другим – к узлу, выделенному синим цветом.
Таким образом, эквивалентная схема состоит из тр¸х последовательно соедин¸нных участков: 1) три параллельно соедин¸нных проводника; 2) затем ещ¸ шесть; 3) и, наконец, снова три (рис. 27).
Ðèñ. 27
Аналогично произвед¸нному в задаче 3 расч¸ту сопротивление тр¸х параллельно соедин¸нных проводников равно 2 Ом, а у шести таких же проводников – вдвое меньше: 1 Ом. Теперь эквивалентная схема состоит из тр¸х последовательно соедин¸нных проводников, и их общее сопротивление
R (2 1 2) Ом 5 Ом.
Ответ: 5 Ом.
Заключение
Итак, подвед¸м краткий итог. При определении общего сопро-
тивления электрической цепи надо попытаться отыскать в ней те проводники, которые соединены друг с другом последовательно либо парал-
лельно. Заменяя их проводниками с эквивалентным сопротивлением, получить более простую схему цепи. Затем продолжить упрощение до тех пор, пока в схеме не оста¸тся лишь один тип соединения – последова-

42 Физика
тельное или параллельное. Попутно нужно находить эквивалентные сопротивления.
Если же не уда¸тся определить ни одной пары проводников, которые были бы соединены последовательно или параллельно, то нужно поискать симметрию в предложенной схеме. Если симметрию удастся найти, то можно использовать один из основных методов преобразования схемы, каждый из которых не изменяет сопротивления цепи.
1. Метод склеивания узлов. Если два или более узлов имеют одинаковый потенциал, то их можно соединить в один узел.
2.Метод исключения участков цепи. Проводник можно удалить, если через него не теч¸т ток (узлы, которые он соединяет, имеют одинаковый потенциал).
3.Метод разрезания узлов. Действие, противоположное склеиванию узлов.
А что делать в том случае, если число проводников в цепи стремится
êбесконечности или не уда¸тся найти не только последовательно или параллельно соедин¸нные проводники, но и симметрию в схеме? Об этом будет рассказано в другой статье.
Ответ на пример 2
Ж¸лтым цветом выделены последовательно соедин¸нные проводники, зел¸ным – параллельно соедин¸нные.
Ðèñ. 28
Задачи для самостоятельного решения
1. В цепи, схема которой изо- |
рой показана на рис. 19, если каж- |
|||||||||||||||||||
бражена на рисунке 29, все провод- |
дый проводник имеет сопротивление |
|||||||||||||||||||
ники имеют сопротивление 8 Ом. |
15 Ом. (Ответ: 7 Ом.) |
|||||||||||||||||||
Определите общее сопротивление |
3. В каждое из р¸бер куба вклю- |
|||||||||||||||||||
цепи. (Ответ: 13 Ом.) |
|
|
|
|
|
|
|
|
|
|
чен проводник сопротивлением 8 Ом. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чему равно сопротивление полу- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чившейся конструкции между вер- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
шинами, принадлежащими одной из |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
граней и лежащими на концах е¸ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
диагонали (на рис. 26 это вершины |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А и 6)? (Ответ: 6 Ом.) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. Определите сопротивление ме- |
|
Ðèñ. 29 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
жду точками А и В цепи, схема ко- |
||||||||||||
2. Определите сопротивление ме- |
||||||||||||||||||||
торой изображена на рис. 30, если |
||||||||||||||||||||
жду точкам А и О цепи, схема кото- |
||||||||||||||||||||
|
||||||||||||||||||||
