Nesterenko / 13_л алг маршрут
.pdf
Определение оптимальных маршрутов в сетях связи
1.Матричный метод маршрутизации в сетях с коммутацией каналов.
2.Алгоритмы маршрутизации в сетях с коммутацией пакетов.
1. Матричный метод маршрутизации в сетях с коммутацией каналов
Матричный алгоритм осуществляет поиск оптимальных путей (по критерию минимальной длины) при ограничениях на максимальное число транзитных центров коммутации в пути. В его основе лежит метод определения длин кратчайших путей между всеми узлами сети, основанный на применении операций над матрицами расстояний.
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
l11 |
l12 |
l13 |
l14 |
|
|
0 |
5 |
|
40 |
|
5 |
10 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||
L |
l21 |
l22 |
l23 |
l24 |
|
|
5 |
0 |
10 |
20 |
1 |
20 |
3 |
l31 |
l32 |
l33 |
l34 |
|
|
|
10 |
0 |
80 |
||||
|
|
|
|
|
|
|
|||||||
|
l41 |
l42 |
l43 |
l44 |
|
|
40 |
20 |
80 |
0 |
|
40 |
80 |
|
|
|
|
4 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для определения |
длин кратчайших путей |
между |
всеми |
||||||||||
узлами сети матрица расстояний L возводится в степень r=N – 1 , где N – число узлов сети.
Правила возведения матрицы L в степень r: |
|
|
|||||
|
операция умножения элементов матрицы соответствует их |
||||||
|
алгебраической сумме: l |
l |
|
l |
l |
|
|
|
|
ik |
|
kj |
ik |
|
kj |
|
сложение элементов матрицы: |
|
|
|
|
||
lij |
l ji |
0 0 0 0 |
0 |
|
lij |
|
|
Значение элемента новой матрицы принимается по критерию минимума длины ветвей:
lij2 |
min lik1 |
lkj1 |
min li1 |
l1 j ; li 2 |
l2 j ;...; liN |
lNj |
|
k 1,2,...,N |
|
|
|
|
|
Дополнительные операции:
1.Формирование матриц очередности выбора исходящих ветвей (статических детерминированных таблиц маршрутов) для каждого центра коммутации.
2.Проверка и исключение наличия петель в путях первого, второго, третьего выбора.
l112
l122
l132
l142
5 |
2 |
10 |
|
|
|
|
l11 |
|
l12 |
||
|
|
|
|
|
|||||||
|
|
|
|
|
|
||||||
1 |
20 |
|
|
3 |
L |
|
l21 |
|
l22 |
||
|
|
|
l31 |
|
l32 |
||||||
|
|
|
|
|
|
|
|
|
|||
40 |
|
80 |
|
|
|
|
l41 |
|
l42 |
||
|
4 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
min l11 |
l11 ; l12 |
|
|
l21 ; l13 |
l31 ; l14 |
|
l41 |
||||
min l11 |
l12 ; l12 |
|
|
l22 ; l13 |
l32 ; l14 |
l42 |
|||||
min l11 |
l13 ; l12 |
|
l23 ; l13 |
l33 ; l14 |
l43 |
||||||
min l11 |
l14 ; l12 |
|
l24 ; l13 |
l34 ; l14 |
|
l44 |
|||||
|
|
|
|
|
5 |
15 |
25 |
|
|||
|
|
|
0 |
|
|
|
|||||
L2 |
L3 |
|
5 |
|
|
0 |
10 |
20 |
|
||
|
15 |
|
10 |
0 |
|
30 |
|
||||
|
|
|
|
|
|
||||||
|
|
|
25 |
|
20 |
30 |
0 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
l13 |
l14 |
|
0 |
5 |
|
40 |
l23 |
l24 |
|
5 |
0 |
10 |
20 |
l33 |
l34 |
|
|
10 |
0 |
80 |
l43 |
l44 |
|
40 |
20 |
80 |
0 |
min 0 |
0 ; 5 5 ; |
; 40 |
40 |
0 |
|
min 0 |
5 ; 5 |
0 ; |
10 ; 40 |
20 |
5 |
min 0 |
; 5 |
10 ; |
0 ; 40 |
80 |
15 |
min 0 |
40 ; 5 |
20 ; |
80 ; 40 |
0 |
25 |
L3 |
L2 |
L1 |
|
lij3 |
min |
lik2 |
lkj1 |
|
k 1,2,..., N |
|
|
2. Алгоритмы маршрутизации в сетях с
коммутацией пакетов
Алгоритм Дейкстры - в процессе выполнения операций определения искомого оптимального пути между заданной парой вершин графа, определяет оптимальные пути от начальной вершины до любых других вершин.
Шаг 1. Формирование начальных условий (матрица весов, вектор путей, множество вершин). Все множество вершин разбивается на два подмножества (1. только начальная вершина; 2. все остальные вершины).
W 
wij 
DН 
d 1 , d 2 ,...,d n
T V1 ,V2 ,...,Vn \VН
Шаг 2. Определение очередной вершины, исключаемой из множества Т.
wнi opt wнj
V j T
Шаг 3.Корректировка матрицы весов W и вектора путей DH.
wнj opt wнj , wнi , wij
Символ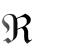 
- некая обобщенная операция, выполняемая над
характеристиками (весами) двух смежных ребер, в результате чего должна получиться характеристика пути, состоящего из этих ребер.
Если wнj изменит свое значение, то есть если wнj wнi , wij , то d(j)=i. В противном случае соответствующий элемент вектора DH не изменяется.
Шаг 4.Определение конца процесса.
Если мощность множества Т равна единице, то все оптимальные пути найдены. В противном случае осуществляется переход к выполнению шага 2.
2
5 |
|
10 |
|
l11 |
l12 |
l13 |
l14 |
|
0 |
5 |
|
40 |
1 |
20 |
3 |
L |
l21 |
l22 |
l23 |
l24 |
|
5 |
0 |
10 |
20 |
l31 |
l32 |
l33 |
l34 |
|
|
10 |
0 |
80 |
||||
|
|
|
|
|
|
|||||||
40 |
|
80 |
|
l41 |
l42 |
l43 |
l44 |
|
40 |
20 |
80 |
0 |
|
4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Первая итерация
Шаг 1. Формирование начальных условий.
|
VН |
V1 |
|
D1 |
|
|
|
T |
2,3,4 |
\ 1 |
|
|||
|
|
|
1,1,1,1 |
|
|
|
||||||||
Шаг 2. |
Определение |
|
|
|||||||||||
очередной вершины, исключаемой из |
||||||||||||||
|
множества Т. |
l |
1i |
min l |
1 j |
min 5, ,40 |
5 |
|
|
|||||
|
|
|
|
V j T |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
V2 |
|
T |
T |
3,4 |
||
|
|
|
|
|
|
|
|
|
i 2 |
|
||||
Шаг 3.Корректировка матрицы весов W и вектора путей DH. |
|
|||||||||||||
l13 |
min l13 , l12 |
l23 |
min , 5 |
10 |
15 |
l13 |
l13 |
d 3 |
2 |
|||||
l14 |
min l14 ,l12 |
l24 |
min 40, 5 |
20 |
25 |
l14 |
l14 |
d 4 |
2 |
|||||
Шаг 4.Определение конца процесса.
T 2 1 |
l1 j |
0 5 15 25 |
D1 |
1,1,2,2 |
|
|
|
|
|
2
5 10
1 |
20 |
3 |
40 80
4
|
|
5 |
|
40 |
|
l1 j |
0 5 15 25 |
|
0 |
|
|
||||
L |
5 |
0 |
10 |
20 |
|
|
|
|
10 |
0 |
80 |
|
|
|
|
|
|
|
|
|
|||
|
40 |
20 |
80 |
0 |
|
|
|
|
|
|
|
|
|
|
|
Вторая итерация
Шаг 2. Определение очередной вершины, исключаемой из множества Т.
l1i |
min l1 j |
min 15,25 15 |
i 3 |
V3 |
T |
T |
4 |
|
Vj T |
|
|
|
|
|
|
Шаг 3.Корректировка матрицы весов W и вектора путей DH. |
|
||||||
l14 |
min l14 , l13 |
l34 min 25, 15 80 |
25 |
l14 |
l14 |
d 4 |
2 |
Шаг 4.Определение конца процесса.
T 1 |
l1 j |
0 5 15 25 |
D1 |
1,1,2,2 |
|
|
|
|
|