
Nesterenko / 8_л_ отн модуляция
.pdf
Помехоустойчивость дискретных сообщений
Помехоустойчивость дискретного канала связи определяется
вероятностью ошибочного приема |
сигналов pош. |
|
|
|
|||||||||
Формула, характеризующая вероятность ошибочного приема S1(t) |
|||||||||||||
(т.е. принятия решения о |
|
|
передаче |
S2(t), когда передавался |
|||||||||
S1(t)), будет следующей: |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E0 |
|
|
|
|
E1 E2 2E12 |
|
|||||
p 1 F |
|
|
1 |
F |
|
|
|||||||
|
|
|
|||||||||||
ош |
|
2N0 |
|
|
|
|
|
2N0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
где F(x) |
– функция |
дополнение |
к |
нормальному |
закону |
||||||||
распределения, которая табулирована в справочниках; N0 – спектральная плотность мощности помех;
E0 – эквивалентная энергия сигнала.
Энергия первого, второго сигналов и взаимную энергию:
|
|
T |
|
|
|
|
T |
|
t dt |
|
T |
|
t S |
|
t dt |
E1 |
|
2 |
|
E |
2 |
|
|
S 2 |
E |
|
S |
2 |
|||
|
S1 |
t dt |
|
|
2 |
|
12 |
1 |
|
|
|||||
|
|
0 |
|
|
|
|
0 |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Встречаются выражения для pош связанных с функцией Крампа:
Ф x |
2 |
|
x |
|
2 |
|
|
|
e |
2 |
dz |
||||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
2 0 |
|
|
|
||
или функцией нормированного центрированного нормального
распределения: |
|
|
x |
|
2 |
|
|
Ф0 x |
1 |
|
|||||
|
e |
|
2 |
dz |
|||
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
2 0 |
|
|
|
||
а также интегральной функцией нормального распределения:
F x |
1 |
x |
|
2 |
|
e |
|
|
2 dz |
||
|
|
|
z |
|
|

 2
2
Взаимосвязь этих выражений:
Ф x 2 Ф0 x |
F x 0,5 Ф0 x |
Оценим влияние структуры передаваемых сигналов на вероятность их ошибочного приема.
Если сигналы близки по форме S1(t)≈S2(t),то E1=E2+E12,
E0=0, из таблиц известно, что F(0)=0,5 следовательно pош=0,5. Такие сигналы разделить сложно. Поэтому применение сигналов, близких по форме, нецелесообразно.
Рассмотрим сигналы с пассивной паузой (АМн сигналы):
S1(t)=S(t), S2(t)=0.
Тогда энергия первого сигнала равна E1=E, а энергия второго и взаимная энергия сигналов равны нулю: E2=E12=0, тогда E0=E. Вероятность ошибки определяется выражением:
s1 t |
|
S1 t |
|
t |
t |
0 |
T |
T |
s2 t |
|
S2 t |
|
t |
t |
0 |
T |
T |
|
|
|
|
|
|
|
|
|
|
E |
|
||
p |
|
1 F |
|
|
|
|
|
|
|||||
|
ош |
|
2N0 |
|
|
|
|
|
|
|
|
||
Сигналы с пассивной паузой

Для ортогональных сигналов S1(t) и S2(t). Пусть E1=E2=E. Согласно условию ортогональности E12=0, тогда E0=2E. Вероятность ошибки при этом будет:
s1 t |
|
S1 t |
|
t |
t |
0 |
T |
T |
s2 t |
|
S2 t |
|
t |
t |
0 |
T |
T |
|
|
|
|
|
|
|
|
|
|
E |
|
||
p |
|
1 F |
|
|
|
|
|
|
|||||
|
ош |
|
N0 |
|
|
|
|
|
|
|
|
||
Ортогональные сигналы
Для противоположных сигналов (противофазных) S1(t)=S(t) и
S2(t)=-S(t). Тогда E1=E2=E, E12=-E, E0=4E.
Вероятность ошибки определяется выражением:
s1 t |
|
S1 t |
|
t |
t |
0 |
T |
T |
s2 t |
|
S2 t |
|
t |
t |
0 |
T |
T |
|
|
|
|
|
|
|
|
|
|
2E |
|||
p |
|
1 F |
|
|
|
|
|
|
|||||
|
ош |
|
|
|
|
|
|
|
|
N0 |
|||
Противоположные (противофазные) сигналы
Часто для быстрого приближенного вычисления функции Лапласа |
||||||||||||||||||
используется формула Тамма и Гомозовой: |
|
|
|
|
|
|
|
|||||||||||
pкг |
0,65 exp 0,443 h 0,75 2 |
|||||||||||||||||
ош |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 p |
|
|
||
|
|
|
|
|
|
p |
КГ |
|
: 2 p |
КГ |
|
КГ |
||||||
2, |
|
|
при ФМн; |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
ОФМн |
|
|
ФМн |
|
|
|
ФМн |
|
||||
1, |
|
|
при ЧМн;рош |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
при АМн. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
0.01 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
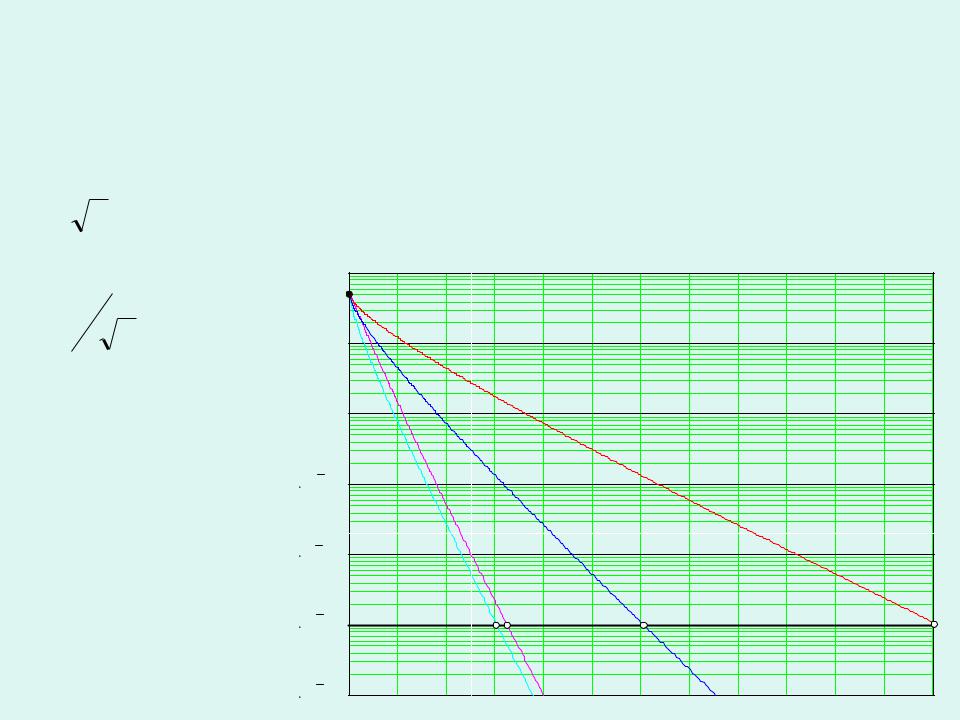
Сигналы |
|
|
|
Сигналы |
|
|
|
Сигналы |
|
|||
|
|
|
4 |
|
противофазные |
|
ортогональные |
|
с пассивной паузой |
|||||||||
|
|
|
1 10 |
|
|
ФМнкг |
ОФМнкг |
ЧМнкг |
|
|
|
|
АМнкг |
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h2 |
|
|
|
1 10 |
0 |
3 |
|
6 |
9 |
12 |
15 |
18 |
21 |
24 |
27 |
30 |
|
33 |
36 |
|
|
|
|
|
|
|||||||||||||
