
ЭНЕРГОСБЕРЕЖЕНИЕ / Energosberezhenie_2005
.pdf
60
где Р – мощность, подведенная из сети; РП – мощность потерь;
РМ – мощность, преобразованная в механическую работу.
Рис.3.2. Механическая характеристика асинхронного двигателя M(ω) и соответствующая ей зависимость тока статора I(ω)
Способ регулирования частоты вращения асинхронного двигателя путем изменения параметров статорной и роторной цепей используется редко. Так, ввод добавочного сопротивления в цепь статора приводит к уменьшению критического скольжения SK и критического момента MK, что обусловливает ограничение диапазона регулирования D = ωmax/ωmin величиной 1,1…1,3. При использовании асинхронного двигателя с фазным ротором при введении добавочного сопротивления в цепь ротора диапазон регулирования существенно расширяется до D = 2…3, но при этом существенно возрастают и потери энергии, пропорциональные величине скольжения S.
Ограниченные возможности регулирования частоты вращения асинхронного двигателя путем изменения напряжения источника питания U связаны с существенным снижением при таком регулировании критического момента и перегрузочной способности двигателя. Этот способ регулирования частоты вращения асинхронных двигателей практически не используется.
61
Наиболее эффективным способом управления скоростью вращения асинхронного двигателя является частотное регулирование, при котором частота и напряжение питания двигателя могут изменяться в соответствии с установленным соотношением независимо друг от друга.
Принцип реализации такого способа определяется тем, что скорость вращающегося магнитного поля статора ω0 пропорциональна частоте источника питания f. Следовательно, изменяя частоту f, можно плавно и в широких пределах регулировать скорость вращения ротора. При этом скольжение S изменяется незначительно и, следовательно, потери РП, пропорциональные скольжению, также изменяются незначительно. Это важное преимущество частотного управления асинхронным двигателем позволяет реализовать энергосберегающие технологии как для двигателей с фазным ротором, так и с короткозамкнутым.
Из изложенного вытекает, что для частотно-регулируемого асинхронного привода требуется, прежде всего, источник переменного тока регулируемой частоты. При появлении в последние десятилетия таких источников на основе статических полупроводниковых преобразователей частоты возникла реальная возможность создания частотно-регулируемых промышленных электроприводов. Их основу составляет преобразователь частоты и асинхронный двигатель.
3.2. Преобразователи частоты в системах электропривода переменного тока
Всистемах электропривода переменного тока широко используются преобразователи частоты с двухступенчатым преобразованием энергии, выполненные на основе выпрямителя трехфазного переменного напряжения сети и автономного инвертора, преобразующего выпрямленное напряжение в напряжение трехфазного переменного тока с регулируемой частотой и амплитудой.
Вкачестве инверторов, как правило, используются автономные инверторы напряжения (АИН). При использовании в таких преобразователях неуправляемого выпрямителя обеспечивается достаточно высокое значение cosφ на входе, но низкое значение коэффициента
62
нелинейных искажений КИ тока, потребляемого из сети. Поскольку коэффициент мощности
КМ = КИ cosφ ,
то его значение снижается при использовании неуправляемого выпрямителя.
Выходное напряжение регулируется методом широтноимпульсной модуляции (ШИМ).
Тормозные режимы в частотно-регулируемых электроприводах осуществляются по принципу динамического торможения при питании обмотки статора постоянным током. В случаях, когда эффективность такого торможения оказывается недостаточной, может быть использован принцип генераторного торможения с передачей активной мощности через АИН в цепь постоянного тока преобразователя частоты. Поскольку передача энергии в сеть через неуправляемый выпрямитель невозможна, для предотвращения недопустимого повышения напряжения на емкости фильтра постоянного тока ее рассеивают на тормозных резисторах с помощью транзисторного импульсного регулятора.
Таким образом, оптимальную по энергетическим показателям и регулировочным и механическим характеристикам структуру современного частотно-регулируемого асинхронного электропривода следует выполнять на основе преобразователя частоты с промежуточным звеном постоянного тока (рис.3.3). Преобразователь частоты состоит из выпрямителя с индуктивно-емкостным фильтром постоянного напряжения и автономного инвертора напряжения, построенного на силовых транзисторах и формирующего основную гармонику выходного напряжения методом широтно-импульсной модуляции.
Преобразователи частоты строятся, как правило, по структурной схеме со звеном постоянного тока, образованным так называемым «бестрансформаторным входом». Наличие неуправляемого или управляемого выпрямителя с емкостным фильтром определяет низкую электромагнитную совместимость преобразователя с питающей сетью. Задачу повышения коэффициента мощности бестрансформаторных преобразователей следует считать одной из существенных при создании технических средств энергосбережения. Повысить

63
электромагнитную совместимость с питающей сетью и обеспечить максимальный коэффициент мощности преобразователей можно на основе принципа двойной модуляции энергетического потока.
Рис.3.3. Структурная схема преобразователя частоты с промежуточным звеном постоянного тока
Рассмотрим существо двойной модуляции на примере реализации электропривода с асинхронным двигателем и импульсномодуляционным преобразователем (ИМП) с промежуточным звеном постоянного тока (рис.3.4). В этом преобразователе переменное напряжение каждой фазы на входе преобразуется полностью управляемым выпрямителем (модуляционным преобразователем) М1 в модулированное повышенной частотой напряжение, длительность импульсов которого изменяется в соответствии с управляющим воздействием UУj(t). Напряжения трех фаз суммируются и образуют промежуточное звено постоянного тока. Напряжение конденсатора С преобразуется инверторными стойками преобразователя М2 в многофазную систему напряжений с требуемыми параметрами в соответствии с UУi(t).
Рис.3.4 Структурная схема электропривода с двойной модуляцией
64
Энергетический вход и выход каждой модуляционной ячейки связаны между собой через коммутационную функцию КФ, вид которой определяется управляющим сигналом модуляционного преобразователя:
U |
ВЫХ |
= КФ(U |
У |
)U |
|
ü |
, |
|
|
|
ВХ ý |
||||
IВХ = КФ(UУ )IВЫХ |
þ |
|
|||||
где UВХ , IВХ – напряжение и ток входного источника;
UВЫХ , IВЫХ – напряжение и ток на выходе ИМП;
КФ( UУ ) – коммутационная функция ИМП, определяемая сигна-
лом UУ.
При двойной модуляции симметричная многофазная система переменных напряжений
UВХ j = U m sin(ω t + ϕ j ) ,
(где j = 1,2,3 для трехфазной системы) модулируется в общем случае симметричной многофазной системой управляющих воздействий той же частоты
UУ j = μ sin(ω t + q j ) ,
где μ – глубина модуляции;
q j – фазовый сдвиг модулирующего воздействия.
Вклад каждой фазы U1 , U2 , U3 в напряжение звена постоянного тока можно представить как
U j = U m КФ j (t) sin (ω t + ϕ j ) .
Полученные таким образом напряжения разных фаз суммируются и на конденсаторе фильтра выделяется напряжение UΣ , которое без учета падения напряжения на фильтре будет равно
3
UΣ = å Um КФ j ( t ) sin ( wt + j j ).
j=1
65
Полученное в звене постоянного тока напряжение подвергается вторичной модуляции в соответствии с другой системой управляющих сигналов
UУ i = μ i sin(ΩC t + θ i ) ,
где индексам i соответствуют параметры, определяющие требуемые выходные напряжения с амплитудой μ i , частотой ΩC и фазой θi.
На рис.3.5–3.7 показаны результаты моделирования на ЭВМ переходных процессов пуска асинхронного электропривода с преобразователем частоты на основе двойной модуляции. В качестве параметров фильтра принимались значения сопротивления R=10-1 Ом, индуктивности L=10-3 Гн и емкости С=10-3 Ф. Моделировался процесс пуска электродвигателя 4А100/4SY3 при напряжении Um=311 В и угловой частоте питающей сети ω=314,16 с-1 . Напряжение сети преобразовывалось с помощью преобразователя М1 в напряжение с пониженной до 225 В амплитудой и частотой 188,5 с-1 формированием соответствующих управляющих воздействий UУj и UУi. Результаты моделирования показаны в виде зависимостей от времени фазных напряжений и токов, момента и частоты вращения двигателя.
Между первой гармонической напряжения на выходе ИМП и током двигателя есть сдвиг (рис.3.6), определяемый свойством асинхронного двигателя расходовать на создание магнитного поля реактивную энергию, потребляя ее из сети. Однако при двойной модуляции энергетического потока эта энергия не потребляется из сети, а перераспределяется соответствующим образом с помощью междуфазного обмена через звено постоянного тока. Угол между напряжением сети и потребляемым из нее током близок к нулю и определяется только конечной частотой импульсной модуляции, равной в нашем случае 900 Гц.
С увеличением кратности квантования все большую долю общей энергии несет первая гармоника. Это позволяет без ущерба для точности использовать приемы усреднения и заменить коммутационные функции КФi(t) и КФj(t) их непрерывными составляющими МФi(t) и МФj(t). В этом случае возможно аналитическое описание процессов в ИМП, на основе которого можно проводить исследование энергетических характеристик электропривода как предельно достижимых при стремлении к бесконечности числа зон и частоты модуляции.

66
Рис.3.5. Фазные токи и напряжения на входе ИМП
Рис.3.6. Фазные токи и напряжения на выходе ИМП
М, Н×м
Рис.3.7. Момент и частота вращения двигателя
67
Допустим, что требуется воспроизвести на выходе М2 двухфазную систему переменных напряжений
U i = U sin (Ωc t + θ i) ,
а входная сеть задана трехфазной системой переменных напряжений
UВХ j =Um sin (ω t+ϕ j).
Согласно алгоритму двойной модуляции, под действием модулирующих воздействий, совпадающих по фазе и амплитуде с напряжением сети, на выходе блока М1 (см.рис.3.2) будут действовать напряжения
UВЫХ j = Um sin (ω t+ϕ j) МФ1(t) = Um sin2 (ω t+ϕ j) ,
которые суммируясь образуют идеальное (без низкочастотных пульсаций) звено постоянного тока
UΣ=Um[sin2ωt+sin2(ωt+120)+sin2(ωt+240)]= =Um[ 0,5 - 0,5 cos2ω t+ 0,5 - 0,5 cos (2ωt+1200) + + 0,5 - 0,5 cos(2ωt+2400)] = 1,5 Um.
По выражению в квадратных скобках можно видеть, что этот процесс сопровождается суммированием постоянных составляющих и взаимной компенсацией составляющих удвоенной частоты.
Вторичная модуляция напряжения позволяет получить на выходе ИМП систему напряжений
UВЫХ i = UΣ МФ2(t) = 1,5 Um sin ( Ωct + θ i ) .
Для двухфазной нагрузки угол θ I = 00, а θ 2 = 900 , поэтому на выходе М2 действуют напряжения
UВЫХ1 = Um sin Ωct;
UВЫХ2 = Um cos Ωct.
68
Пусть под действием этих напряжений в симметричной активноиндуктивной нагрузке протекают токи
IВЫХ 1 = Im sin (Ωct + γ ),
IВЫХ2 = Im cos (Ωct + γ ).
Каждая фаза вносит вклад в ток звена постоянного тока, определяемый формулой
I 0 = IВЫХ i МФ2(t) = Im sin (Ωc t + γ i ) sin (Ωc t + θ i ),
в частности
I 01 = Im sin (Ωc t + γ i ) sin Ωc t = Im /2 [cos γ - cos (2Ωct + γ )]; I 02 = Im cos (Ωc t + γ i ) cos Ωc t = Im /2 [cos γ + cos (2Ωct + γ )].
В звене постоянного тока со стороны нагрузки будет протекать ток IΣ , равный сумме токов I 01 и I 02. Нетрудно показать, что в этом звене будет выделена постоянная составляющая тока, также не зависящая от времени и равная IΣ = Im cosγ i , а сумма переменных составляющих удвоенной частоты будет равна нулю за счет включения их в общий контур в звене постоянного тока и взаимной компенсации.
Таким образом, осуществляются преобразование активной составляющей тока нагрузки в ток звена постоянного тока и взаимная компенсация реактивной составляющей тока нагрузки.
С учетом сказанного потребляемый из сети ток будет равен
IВХ j = IΣ (t) cos γ i sin (ω t+ϕ j ).
Из последнего выражения следует, что из сети потребляется только активная составляющая тока многофазной нагрузки, пропорциональная косинусу угла нагрузки, а реактивная составляющая тока нагрузки циркулирует между фазами и замыкается в общих узлах М2.
Рассмотренные процессы иллюстрируются временными диаграммами (рис.3.8), построенными по приведенным соотношениям.

69
u, i
u
u, i 
i
i
i
UA |
UB |
UC |
iA |
iB |
iC |
|
|
 ω t
ω t
а)
UΣ
Umsin2(ωt) Umsin2(ωt+1200) Umsin2(ωt-1200)
ω t
б)
 U1=UΣsin(ΩCt)
U1=UΣsin(ΩCt)
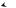 i1
i1
в)
i2 |
i1 |
ia1 |
ip1 |
ia2
ia1sin2(ΩCt)
 ip1sin2(ΩCt)
ip1sin2(ΩCt)
iΣ г)
ia2cos2(ΩCt)
д)  ip2cos2(ΩCt)
ip2cos2(ΩCt)
U2 =UΣcos(ΩCt)
 i2
i2
ω t
 ω t
ω t
ip2
ω t
 ω t
ω t
е)
Рис. 3.8. Мгновенные значения токов и напряжений:
а – на входе М1; б,д,е – в звене постоянного тока; в,г – на выходе М2
