Расчет теплоотдачи при естественной конвекции жидкости. Задание №3 Вариант 4

Через плоскую прослойку теплоносителя(воздух) передается теплота от поверхности с температурой к поверхности с температурой . Толщина прослойки.

Рассчитать плотность теплового потока .

Для воздушной прослойки учесть лучистый теплообмен между поверхностями, приняв что расстояние между ними мало по сравнению с их размерами. Степень черноты поверхностей ,.

При расчете плотности теплового потока когда теплоносителем является воздух необходимо учитывать помимо отдачи тепла конвекцией, также отдачу тепла излучением. Формула для расчета плотности теплового потока будет иметь вид:

,

Теплоотдача при естественной конвекции в ограниченном объеме зависит от многих факторов, в том числе от толщины () и формы прослойки, от физических свойств жидкости или газа в прослойке.

Теплота переданная конвекцией через прослойку жидкости или газа, для плоских прослоек рассчитывается по уравнению:

, Вт/м²

где:

, м – толщина прослойкивоздуха.

- температуры стенок.

,- эквивалентный коэффициент теплопроводности, учитывающий передачу тепла через прослойку теплопроводностью и конвекцией.

- коэффициент характеризующий влияние конвекции на перенос тепла , зависит от числа Грасгофа и Прандтля

Определяем значения чисел Грасгофа и Прандтля

где:

, м – толщина прослойкивоздуха.

- температуры стенок.

,- коэффициент кинематической вязкостивоздуха;

,- ускорение силы тяжести;

,- температурный коэффициент объемного расширения для газов, для жидкостей находится по таблицам теплофизических свойств.

Определяющей температурой в уравнении является средняя температура воздуха

,- кинематическая вязкостьвоздухапри найдена путем интерполяции табличных значений [1, стр.403]

- число Прандтля при найден путем интерполяции табличных значений [1, стр.403]

Находим значение произведения числа Грасгофа и Прандтля

Так как значение коэффициентарассчитывается по формуле:

Определяем значение эквивалентного коэффициента теплопроводности

,

,значение теплопроводности воздуха при [1, стр.403] получено путем интерполяции табличных значений.

,

Определяем количество теплоты переданной конвекцией

, Вт/м²

Так как в роли теплоносителя между стенками выступает воздух необходимо также рассчитать количество теплоты переданного от стенки к стенке излучением

Для плоской прослойки воздуха передача тепла излучением между поверхностями с температурой ирассчитывается по уравнению:

, Вт/м²

где:

- температура поверхностей стенок в градусах кельвина

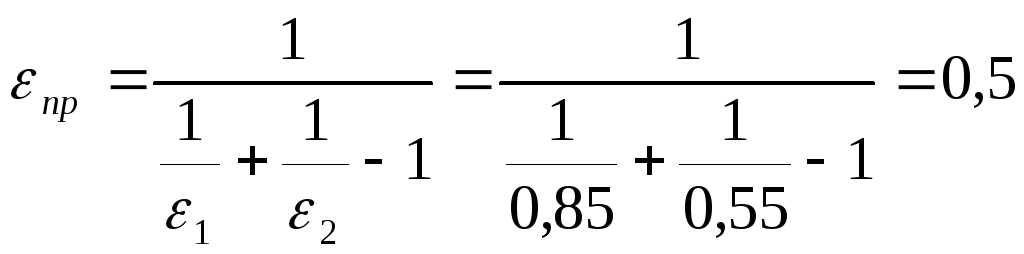- приведенная степень черноты;

- степени черноты поверхностей.

- коэффициент излучения абсолютно черного тела.

Определяем количество теплоты переданного излучением

, Вт/м²

Определяем общее количество теплоты переданного от стенки к стенке через прослойку воздуха.

, Вт/м²

Расчет теплоотдачи при фазовых превращениях. Задание №4 Вариант 4

При пузырьковом кипении воды в условиях естественной конвекции известны давление воды , бара и плотность теплового потока, подводимого к поверхности нагрева , Вт/м²

Рассчитать коэффициент теплоотдачи , используя:

а) уравнения Кружилина;

б) эмпирическую формулу

Оценить (в процентах) отклонение полученных результатов. Рассчитать температуру на поверхности нагрева () и количество испаряющейся жидкости с 1 м² поверхности нагрева за 1 час.

Для расчета среднего коэффициента теплоотдачи при пузырьковом кипении воды в условиях естественной конвекции можно воспользоваться безразмерным уравнением подобия Кружилина Г. Н. либо эмпирическим уравнением зависимости коэффициента теплоотдачи от режимных параметров давления и плотности теплового потока

Определяем температуру насыщения при данном давлении

При давлении насыщения равном бар температура насыщения будет , ºС [2, стр. 111].

Уравнение подобия Кружилина Г.Н. имеет вид:

;

где: ипринимаются в зависимости от значения числа Рейнольдса

при

при

Значение числа Рейнольда находится по уравнению:

;

где: - линейный размер для паровой фазы.

- скорость парообразования.

Определяем величину линейного размера паровой фазы.

,м

где: ,- коэффициент поверхностного натяжения воды при , ºС [2, стр. 111].

,- плотность воды при , ºС [2, стр. 111].

,- изобарная теплоемкость воды при бар [2, стр. 111].

,- температура насыщения при бар, в градусах кельвина.

,- теплота парообразования при бар [2, стр. 112].

,- плотность пара при бар [2, стр. 112].

,м

Определяем скорость парообразования

,

Определяем значение числа Рейнольдса:

где: ,- коэффициент кинематической вязкости воды при , ºС [2, стр. 111].

Так как то формула для расчета значение критерия Нуссельта будет иметь вид:

где: - число Прандтля воды при температуре насыщения , ºС [2, стр. 111].

Через критерий Нуссельта определяем значение коэффициента теплоотдачи

,

где: ,- коэффициент теплопроводности воды при , ºС [2, стр. 111].

Определяем коэффициент теплоотдачи через эмпирическое уравнение зависимости коэффициента теплоотдачи от режимных параметров и.

,

Определяем отклонения полученных коэффициентов теплоотдачи полученных по уравнению Кружилина и эмпирическому уравнению:

Допустимая погрешность уравнения подобия, каким является уравнение Кружилина составляет до 30% и определяется не только погрешностью эксперимента, но и корректностью математического описания задачи.

Температура на поверхности нагрева определяется из уравнения Ньютона-Рихмана:

, ºС

Определяем количество испарившейся жидкости из уравнения теплового баланса, при условии что м².

При расчете количества испарившейся жидкости коэффициент теплоотдачи берется из эмпирического уравнения

,