Первый критерий.

По наблюдениям вычисляют величину

(7)

, (8)

Гипотеза о нормальности принимается если

, (9)

где =0,02 - 0,1 – вероятность ошибки 1 рода (уровень значимости)инаходятся поиn из таблицы 1 (Приложение 2)

Второй критерий

Из таблицы 2 (Приложение 2) по заданным n и определяют два числаиm Гипотеза о нормальности принимается, если не более m разностей превосходят, гдеS рассчитывается по формуле (5), - квантиль нормированной функции Лапласа

См. таблицу 3 (Приложение 2)

Гипотеза о нормальности принимается только в том случае, если для проверяемой группы результатов наблюдений выполняются оба критерия. Уровень значимости составного критерия , где,- уровни значимости для 1 и 2 критерия соответственно.

4. Определить наличие грубых погрешностей, и если последние обнаружены, соответствующие результаты отбросить и повторить вычисления. Сначала следует проверить, не являются ли максимальное и минимальноезначения выборкирезультатами наблюдений с грубыми погрешностями. Приведем критерий такой проверки. ЕслиU<П , то результатов наблюдений с грубыми погрешностями в выборке нет, если U>П , то максимальный или минимальный член (в зависимости от того, который из них обеспечивает наибольшее значение U ) является результатом наблюдений с грубой погрешностью.

Здесь

,(10)

и S рассчитываются по формулам (4) и (5) соответственно ;

- квантили распределения, приведенные в зависимости от (1-q) и n в таблице 4 Приложения 2.

После проверки по указанному критерию результат наблюдений с грубой погрешностью устраняют из выборки и вновь повторяют всю процедуру. Так действуют до тех пор, пока все результаты наблюдений с грубыми погрешностями не будут устранены.

5. Определить оценку величины . Обозначим оценку величины . Поскольку выборочные средние ,,…являются оценками величин,,…, входящих в формулу (3) обозначим их,,…. Тогда оценку величиныможно определить по формуле

. (11)

6. Вычислить доверительные границы случайной составляющей погрешности результатов многократных измерений для всех величин ,,…, подвергаемым прямым измерениям и входящим в зависимость (3)

Доверительную границу (без учёта знака) случайной погрешности результата измерения находят по формуле

, ,(12)

где - квантиль распределения Стьюдента, который в зависимости от доверительной вероятностии числа результатов наблюдений находят по таблице 5 Приложение 2

7. Вычислить доверительные границы неисключенной систематической погрешности (НСП) результатов измерений для каждой величины ,,…НСП результата образуется из составляющих, в качестве которых могут быть НСП метода, средств измерений, а также вызванные другими источниками. При суммировании составляющих НСП результата измерения все они рассматриваются, как случайные величины. При отсутствии данных о виде распределения этих случайных величин их распределения принимают за равномерные. Доверительную границу НСПрезультата измерения при равномерном распределении НСП (без учёта знака) можно вычислить по формуле

,

, ,(13)

где - границаj – ой НСП

- коэффициент, определяемый принятой доверительной вероятностью и числом составляющих НСП(таблица 6,

Приложение 2)

Доверительную вероятность для вычисления доверительной границы НСП принимают той же, что и при вычислении доверительной границы случайной погрешности результата измерения.

8. Вычислить доверительные границы погрешности результатов измерений каждой величины,,…

Если принять, что погрешность от пренебрежения систематической составляющей погрешности результата измерения не должна превышать 15%, то получим предельные отношения . В зависимости о доверительной вероятности, эти отношения равны

0,90 0,95 0,99

1,2 1,1 1,1

Если пренебречь случайной составляющей, ориентируясь на ту же погрешность 15%, то

0,90 0,95 0,99

3 4 7

Таким образом, если , то с достаточной уверенностью можно пренебречь систематической, а если- можно пренебречь случайной составляющей погрешности результата измерения.

Если при заданной доверительной вероятности, то границу погрешности результата измерения(без учёта знака) можно вычислить по формуле

,(14)

где

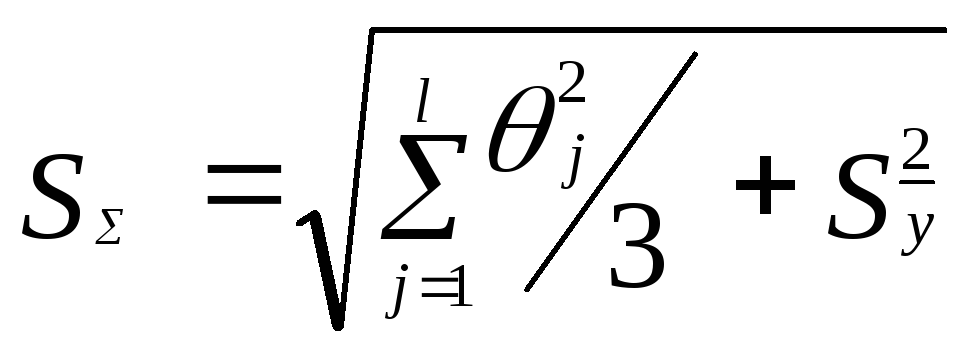,(15)

,(16)

9. Вычислить значения частных производных при найденных ранее (см. п.5) оценках величин,,….

10. Определить доверительную границу погрешности результата косвенного измерения по формуле

,(17)

11. Определить относительную погрешность результата косвенного измерения величиныпо формуле

, (18)

12. Результат косвенного измерения записывается в виде

(19)

Доверительную границу погрешности , а такжеиследует выражать одной или двумя значащими цифрами. Две цифры оставляют при наиболее точных измерениях, а также в тех случаях, когда цифра старшего разряда числа, выражающего погрешность, меньше или равна трем. Отметим, что в промежуточных выкладках при расчете погрешностей нужно удерживать три-четыре значащих цифры. Результат косвенного измерениянеобходимо округлять так, чтобы его значение оканчивалось цифрой того разряда, что ипосле округления.