13

Санкт-Петербургский Государственный Университет Информационных Технологий, Механики и Оптики

Кафедра твердотельной оптоэлектроники

Методические указания

По выполнению расчётной работы на тему:

“ОЦЕНКА ПОГРЕШНОСТИ РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ ПОКАЗАТЕЛЯ ПРЕЛОМЛЕНИЯ ОПТИЧЕСКИХ СРЕД”

Санкт-Петербург

2005 Введение

Проведение оптико-физических измерений должно быть тесно связано с конкретной математической обработкой их результатов. В противном случае возможно не только искажение результатов, но и вообще возникновение принципиально неверных выводов после проведения экспериментальных исследований.

В связи с этим основной целью данной работы является освоение методики статистической обработки результатов эксперимента, которая позволяет оценить погрешность измерений и, следовательно, судить о степени достоверности экспериментальных данных. Оценка погрешности производиться для результатов косвенных измерений показателя преломления оптических сред. Одним из методов измерения N является метод отражательной рефрактометрии, основанный на измерении относительного коэффициента отражения ρ света линейно поляризованного под углом 45⁰ к плоскости падения. При этом расчет показателя преломления N производиться по формуле

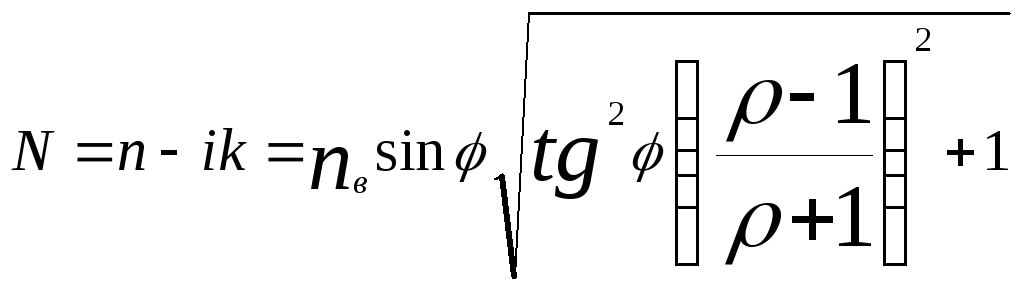^, (1)

Где n – действительная часть показателя преломления,

k – показатель поглощения

- показатель преломления внешней среды (в случае воздуха при нормальных условиях =1,000292),

- угол падения светового пучка

,

где - азимут линейно восстановленной поляризации отраженного пучка,

- разность фаз между ортогональными компонентами эллиптически поляризованного отраженного пучка.

При отсутствии поглощения в исследуемой среде К =0 и =0

Тогда формула (1) примет вид

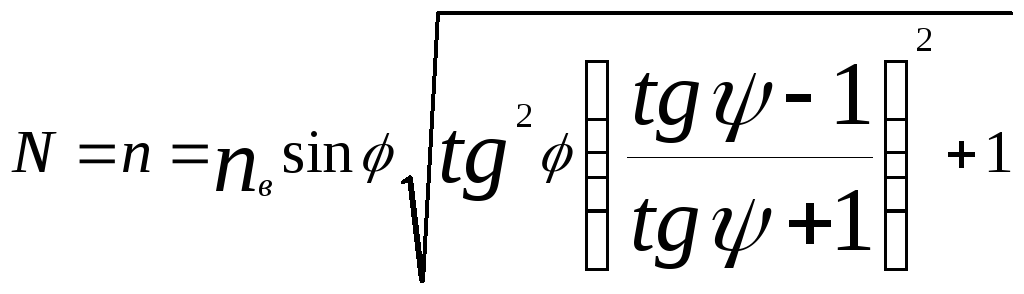(2)

Данные по измерениям величин и , выполненные для различных оптических сред (стекол, кристаллов, полупроводниковых материалов) приведены в Приложении 1

Обработка Результатов наблюдений при косвенных измерениях

Косвенным называется измерение, при котором значение искомой величины находят на основании известной зависимости, связывающей её с другими величинами, которые определяются прямыми измерениями. Обозначим искомую величину , а величины, подвергаемые прямым измерениям,, …,Связь между нами задана в явном виде

, (3)

где F – известная функциональная зависимость

В данной расчётной работе предлагается один из способов обработки результатов наблюдений при косвенных измерениях.

Пусть при прямых измерениях для каждой из величин ,, …,получена группа результатов наблюдений. Процедура обработки состоит из следующих этапов.

Ⅰ. По результатам наблюдений при прямых измерениях величин ,, …,рассчитываются выборочное среднееи оценка среднего квадратического отклонения случайной погрешностидля всех величин,, …,подвергаемых прямым измерениям.

(4)

j = 1,…,m

, (5)

j = 1,…,m

где n – число результатов наблюдений

, , …,- результаты полученные при прямых измерениях величины(ПриложениеⅠ). В дальнейшем индекс j при величинах ,и т. д. будем опускать.

2. Вычислить оценки среднего квадратического отклонения выборочного среднего

(6)

3. Проверить гипотезу о том, что случайная погрешность подчиняется нормальному распределению.

В случае если 15 < n < 50 проверка осуществляется по двум критериям. Гипотеза о нормальности принимается только в том случае, если она принята, как по первому, так и по второму критериям.