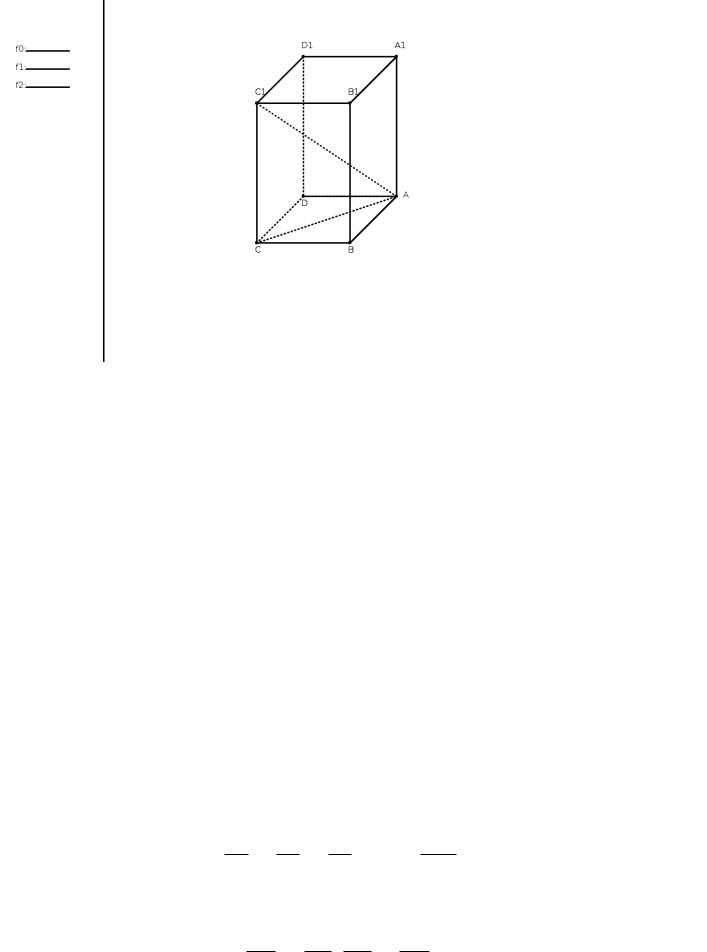
Рис. 1.10: Прямоугольный Параллелепипед
1.3Свойства параллельных сечений в пирамиде
1.3.1Теоремы
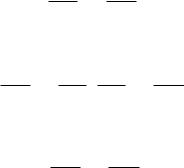
Если пирамида (рис. 1.11) пересечена плоскостью, параллельной основанию, то:
1)боковые ребра и высота делятся этой плоскостью на пропорциональные части;
2)в сечении получается многоугольник (abcde), подобный основанию;
3)площади сечения и основания относятся, как квадраты их расстояний от вершины.
1)Прямые ab и AB можно рассматривать как линии пересечения двух параллельных плоскостей (основания и секущей) третьей плоскостью ASB; поэтому abkAB. По этой же причине bckBC,cdkCD.... и amkAM; вследствие этого
aASa = bBSb = cCSc = ::: = mMSm
2) Из подобия треугольников ASB и aSb, затем BSC и bSc и т. д. выводим:
ABab = BSbS ; BSbS = BCbc ;
16
откуда
ABab = BCbc :
Так же
BCbc = CScS ; CScS = CDcd ;
откуда
BCbc = CDcd
Так же докажем пропорциональность остальных сторон многоугольников ABCDE и abcde.Так как, сверх того, у этих многоугольников равны соответственные углы (как образованные параллельными и одинаково направленными сторонами), то они подобны. Площади подобных многоугольников относятся, как квадраты сходственных сторон; поэтому
|
|
ABCDE |
|
|
AB2 |
|
AB |
)2; |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
= ( |
|
|
|
|||||
|
|
|
abcde |
|
|
|
ab2 |
|
|
|
|
ab |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
но |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
AB |
= |
AS |
= |
MS |
; |
|
|
|
|||||||||||||
|
|
|
|
|
ab |
|
|
|
ms |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
as |
|
|
|
|
|
|
|
|
||||||||
значит |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ABCDE |
|
|
|
MS |
|
|
|
MS2 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
= ( |
|
|
|
)2 = |
|
|
: |
|
||||||||
|
|
|
abcde |
|
|
|
ms |
|
ms2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
set2D(1; 9; 1; 14); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 = tablePlot( |
4 |
1 |
5 |
|
|
9 |
4 |
5 |
); |
|
|
|
|
||||||||||||
1 |
3 |
14 |
|
|
3 |
1 |
14 |
|
|
|
|
||||||||||||||
|
3:3 |
4:5 6:9 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
p2 = tablePlot( |
|
|
); |
|
|
|
|
|
|
|
|
|
|
||||||||||||
p3 = tablePlot( |
9 |
8 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
;0 dash0); |
|
||||||
9 |
7 |
3 |
1 |
6 |
|
|
5 |
|
7 |
3 |
|
5 |
|
||||||||||||
3 |
5 |
5 |
3 |
3 |
|
|
14 |
5 |
5 |
|
14 |
|
|||||||||||||
p4 = tablePlot( |
|
|
: |
: |
4:1 5:9 6:9 |
|
|
|
|
|
|||||||||||||||
595 |
393 |
10 |
|
|
10 |
|
|
|
9 ;0 dash0); |
|
|||||||||||||||
p5 = pointsPlot( |
1 4 9 7 3 3:3 4:5 7 6 6 5:5 5 |
; |
|||||||||||||||||||||||
3 |
1 3 |
|
|
5 |
5 |
9 |
|
|
|
8 |
|
9 |
10 3 9 14 |
||||||||||||
[’A’,’B’,’C’,’D’,’E’,’a’,’b’,’c’,’d’,’M’,’m’,’S’],[6,4,2,2,7,6,5,2,2,2,11,0]); showPlots([p1; p2; p3; p4; p5];0 noAxes0);
17
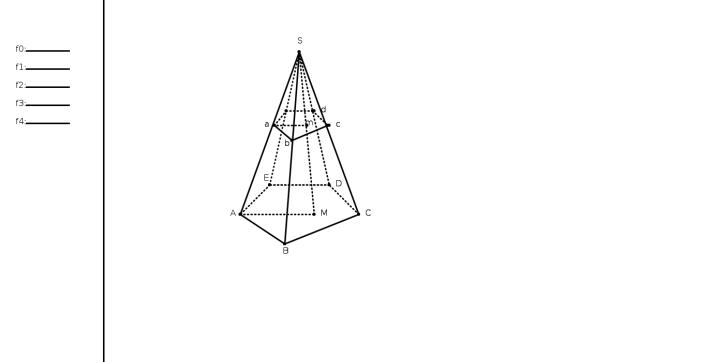
Рис. 1.11: Пирамида
1.3.2Следствие
У правильной усеченной пирамиды верхнее основание есть правильный многоугольник, подобный нижнему основанию, а боковые грани суть равные и равнобочные трапеции (рис. 1.11).
Высота любой из этих трапеций называется апофемой правильной усеченной пирамиды.
1.3.3Теорема
Если две пирамиды с равными высотами рассечены на одинаковом расстоянии от вершины плоскостями, параллельными основаниям, то площади сечений пропорциональны площадям оснований.
Пусть (рис. 1.12) B и B1 площади оснований двух пирамид, H высота каждой из них, b и b1 площади сечений плоскостями, параллельными основаниям и удаленными от вершин на одно и то же расстояние h.
Согласно предыдущей теореме мы будем иметь:
b |
h2 |
|
b1 |
|
|
h2 |
|
|
|
= |
|
|
|
= |
|
|
; |
|
H2 |
|
B1 |
H2 |
||||
B |
|
|
|
|||||
18
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
|
= |
b1 |
|
|
b |
|
= |
|
B |
: |
|
||||
|
|
|
|
B |
|
|
|
|
|
|
B |
|
|
||||||||
|
|
|
|
|
B b |
1 |
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
set2D( 2; 36; 2; 23); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 = tablePlot( |
0 |
7 |
|
10 |
|
0 |
10 |
|
|
13 |
|
|
7 |
); |
|||||||
0 |
23 |
0 |
|
0 |
|
0 |
|
|
5 |
|
|
23 |
|||||||||
p2 = tablePlot( |
25 |
22 |
27 |
|
25 |
34 |
27 |
); |
|||||||||||||
0 |
|
5 |
23 |
|
0 |
|
|
|
5 |
23 |
|||||||||||
|
11:9 |
23:1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p3 = tablePlot( |
|
); |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
12:3 |
22:6 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
p4 = tablePlot( |
|
); |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
7 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
9:3 |
25:2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
p5 = tablePlot( |
|
); |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
13 |
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3:8 |
8:4 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p6 = tablePlot( |
|
|
); |
|
|
|
|
|
|
|
|
|
|||||||||
12 |
|
12 |
|
14 |
|
|
|
|
|
|
|
|
|
|
|||||||
p7 = tablePlot( |
24:6 |
26 |
|
30:3 |
|
); |
|
|
|
|
|
|
|||||||||
14 |
12 |
|
|
14 |
|
|
|
|
|
||||||||||||
|
7 |
7 |
2 |
|
2 |
|
7 |
|
7 |
|
|||||||||||
p8 = tablePlot( |
2 |
1 |
2 |
|
33 |
|
36 |
33 |
|
|
); |
||||||||||
p9 = tablePlot( |
7 |
27 |
|
); |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
23 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
p10 = tablePlot( |
19 |
19 |
;0 arrow0); |
|
15 |
23 |
|
p11 = tablePlot( |
14 |
14 |
;0 arrow0); |
16:6 |
13 |
p12 = tablePlot( |
19 |
19 |
;0 arrow0); |
12:6 |
3 |
p13 = tablePlot( |
14 |
14 |
;0 arrow0); |
|
19 |
23 |
|
p14 = tablePlot( |
0 |
4 |
7 |
;0 dash0); |
|
0 |
5 |
23 |
|
p15 = tablePlot( |
24:5 |
30:3 |
;0 dash0); |
|
14 |
14 |
|
p16 = tablePlot( |
4 |
13 |
;0 dash0); |
|
5 |
5 |
|
p17 = tablePlot( |
4 |
5:6 |
10 |
;0 dash0); |
12 |
14 |
14 |
19
p18 = tablePlot( |
7 |
7 |
11:8 |
;0 dash0); |
23 |
3 |
3 |
p19 = tablePlot( 2:2 12:3 ;0 dash0);
77
|
|
|
|
|
|
|
|
|
|
p20 = tablePlot( |
23:1 |
27 |
27 |
|
;0 dash0); |
|
|||
|
|
3 |
|
3 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p21 = tablePlot( |
22:6 |
33:2 |
;0 dash0); |
|
|
||||
|
|
7 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p22 |
= tablePlot( |
22 |
34 |
;0 dash0); |
|
|
|||
|
|
5 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p23 |
= tablePlot( |
7 |
9:2 |
;0 dash0); |
|
|
|||
13 |
|
13 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
p24 |
= tablePlot( |
27 |
25:2 |
;0 dash0); |
|
|
|||
|
|
13 |
|
13 |
|
|
|
|
; |
|
|
7 |
|
27 |
7 |
27 |
14 |
19 |
|
p25 |
= pointsPlot( 3 |
|
3 |
13 |
13 |
16:6 |
12:6 |
||
[’B’,’B1’,’b’,’b1’,’h’,’H’],[5,2,5,1,0,0]);
showPlots([p1; p2; p3; p4; p5; p6; p7; p8; p9; p10; p11; p12; p13; p14; p15; p16; p17; p18
Рис. 1.12: Две пирамиды
20