
- •МНОГОГРАННИКИ
- •ПАРАЛЛЕЛЕПИПЕД И ПИРАМИДА
- •Многогранник
- •Призма
- •Параллелепипед
- •Пирамида
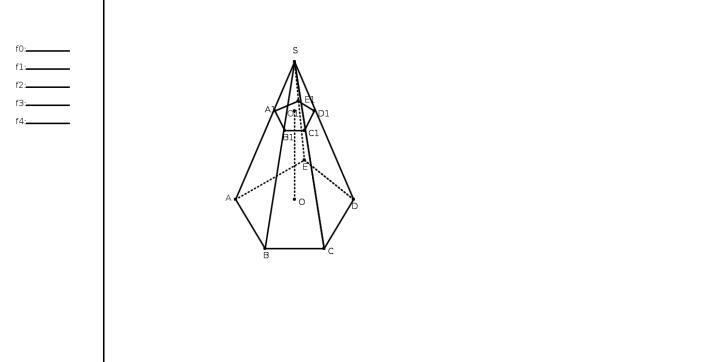
- •Усеченная Пирамида
- •Свойства граней и диагоналей параллелепипеда
- •Теорема
- •Теорема
- •Свойства параллельных сечений в пирамиде
- •Теоремы
- •Следствие
- •Теорема
- •Следствие
- •Боковая поверхность призмы и пирамиды
- •Теорема
- •Следствие
- •Теорема
- •Теорема
- •ОБЪЕМ ПРИЗМЫ И ПИРАМИДЫ
- •Основные допущения в объемах.
- •Единица объёма.
- •Объем параллелепипеда.
- •Теорема
- •Следствие.
- •Лемма
- •Теорема
p3 = tablePlot( |
1 |
8 |
13 |
8 |
7 |
;0 dash0); |
6 |
10 |
6 |
10 |
20 |
p4 |
= tablePlot( |
7 |
|
7 |
;0 dash0); |
|
|
|
|
|
6 |
|
15 |
|
|
|
|
p5 |
= pointsPlot( |
1 |
4 |
10 13 8 |
5 6 8 9 7:4 7 7 |
7 |
; |
|
6 |
1 |
1 6 10 |
15 13 13 15 16 20 6 |
15 |
||||
[’A’,’B’,’C’,’D’,’E’,’A1’,’B1’,’C1’,’D1’,’E1’,’S’,’O’,’O1’],[6,4,3,4,4,6,4,3,3,2.5,0,3,5]); showPlots([p1; p2; p3; p4; p5];0 noAxes0);
Рис. 1.7: Усеченная Пирамида
1.2Свойства граней и диагоналей параллелепипеда
1.2.1Теорема
Впараллелепипеде:
1)противоположные грани равны и параллельны;
2)все четыре диагонали пересекаются в одной точке и делятся в ней пополам.
1)Грани (рис. 1.8)BB1C1C и AA1D1D параллельны, потому что две пересекающиеся прямые BB1 и B1C1 одной грани параллельны двум пересекающимся прямым AA1 и AA1D1 другой; эти грани и равны, так как
12
B1C1 = A1D1,B1B = A1A (как противоположные стороны параллелограммов) и \BB1C1 = \AA1D1 2) Возьмем (рис. 1.9) какие-нибудь две диагонали, например AC1 и BD1, и проведем вспомогательные прямые AD1 и BC1 Так как ребра AB и D1C1 соответственно равны и параллельны ребру DC,то они равны и параллельны между собой; вследствие этого фигура AD1C1B есть параллелограмм, в котором прямые C1A и BD1 диагонали, а в параллелограмме диагонали делятся в точке пересечения пополам. Возьмем теперь одну из этих диагоналей, например AC1 , с третьей диагональю, положим, с B1D Совершенно так же мы можем доказать, что они делятся в точке пересечения пополам. Следовательно, диагонали B1D и AC1 и диагонали AC1 и BD1 (которые мы раньше брали) пересекаются в одной и той же точке, именно в середине диагонали AC1 . Наконец, взяв эту же диагональ AC1 с четвертой диагональю A1C , мы также докажем, что они делятся пополам. Значит, точка пересечения и этой пары диагоналей лежит в середине диагонали AC1. Таким образом, все четыре диагонали параллелепипеда пересекаются в одной и той же точке и делятся этой точкой пополам.
set2D(0; 10; 0; 14); |
|
|
|
|
|
|
|
|
|
|
|
|
|
p1 = tablePlot( |
1 |
1 |
7 |
10 |
4 |
1 |
1 |
4 |
4 |
4 |
10 |
10 |
); |
3 |
11 |
14 |
12 |
9 |
11 |
3 |
1 |
9 |
1 |
3 |
12 |
p2 = tablePlot( |
0:8 |
1:2 |
); |
|
6 |
6 |
|
0:8 1:2
p3 = tablePlot( 5:8 5:8 );
p4 = tablePlot( |
6 |
6 |
); |
9:8 |
10:2 |
3:8 4:2
p5 = tablePlot( 5:8 5:8 );
|
|
3:8 |
4:2 |
|
|
|
|
|
|
|
|
|
|
p6 |
= tablePlot( |
|
); |
|
|
|
|
|
|
||||
|
|
6 |
|
6 |
|
|
|
|
|
|
|
|
|
|
5 |
|
5 |
|
|
|
|
|
|
|
|||
p7 |
= tablePlot( |
|
|
); |
|
|
|
|
|
||||
12:8 |
13:2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p8 |
= tablePlot( |
4 |
4:8 4:7 |
); |
|
|
|
|
|
||||
8:2 |
8:5 |
9:3 |
|
|
|
|
|
||||||
p9 |
= tablePlot( |
1 |
|
1:8 |
|
1:7 |
); |
|
|
|
|||
10:2 |
10:5 |
|
11:3 |
|
|
|
|||||||
|
|
1 |
7 |
7 |
|
7 |
10 |
;0 dash0); |
|
||||
p10 = tablePlot( 3 |
5 |
14 |
|
5 |
3 |
; |
|||||||
|
|
1 |
|
4 |
10 |
7 |
1 |
4 |
10 |
7 |
|||
p11 = pointsPlot( 3 |
|
1 |
3 |
|
5 |
11 |
9 |
12 |
14 |
||||
[’A’,’B’,’C’,’D’,’A1’,’B1’,’C1’,’D1’],[6,4,3,4,0,0,1,0]); showPlots([p1; p2; p3; p4; p5; p6; p7; p8; p9; p10; p11];0 noAxes0);
13
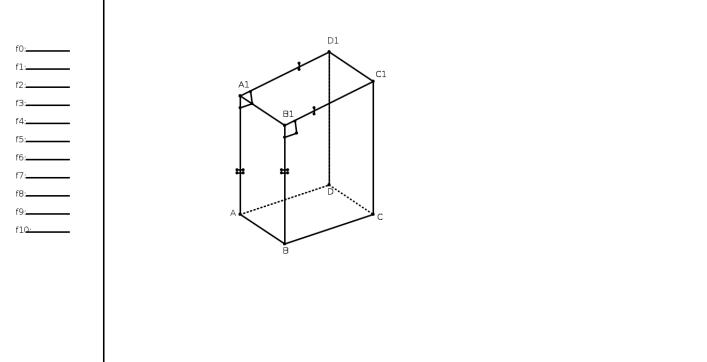
Рис. 1.8: Параллелепипед
set2D(1; 11; 1; 12); |
|
|
|
|
|
|
|
|
|
|
|
|
p1 = tablePlot( |
3 |
1 |
3 |
11 |
9 |
3 |
5 |
3 |
9 |
11 |
5 |
); |
12 |
4 |
1 |
9 |
1 |
1 |
9 |
12 |
12 |
9 |
9 |
p2 = tablePlot( |
3 |
9 |
1 |
11 |
;0 dash0); |
|
1 |
12 |
4 |
9 |
|
p3 = tablePlot( |
3 |
9 |
;0 dash0); |
12 |
1 |
p4 |
= tablePlot( |
1 |
|
7 |
9 |
7 |
9 |
;0 dash0); |
|
||
|
|
4 |
|
4 |
1 |
4 |
12 |
|
|
|
|
p5 |
= pointsPlot( |
1 |
3 |
9 |
7 |
3 |
5 |
11 |
9 |
; |
|
4 |
1 |
1 |
4 |
12 |
9 |
9 |
12 |
||||
[’A’,’B’,’C’,’D’,’A1’,’B1’,’C1’,’D1’],[6,4,3,4.5,0,0,1,0]); showPlots([p1; p2; p3; p4; p5];0 noAxes0);
1.2.2Теорема
В прямоугольном параллелепипеде квадрат любой диагонали(AC1 рис 1.10)равен сумме квадратов трех его измерений.
Проведя диагональ основания AC, получим треугольники AC1C и ACB.Оба они прямоугольные: первый потому, что параллелепипед прямой и, следовательно, ребро CC1 перпендикулярно к основанию; второй потому, что парал-
14
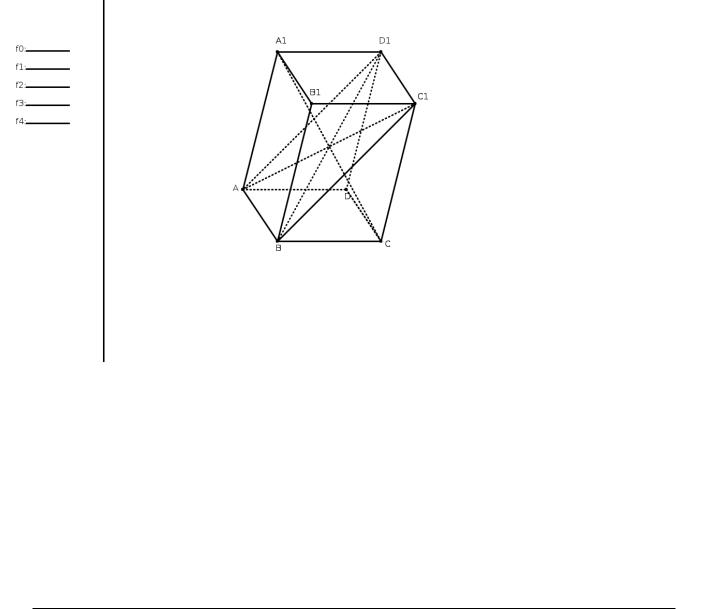
Рис. 1.9: Параллелепипед
лелепипед прямоугольный и, значит, в основании его лежит прямоугольник. Из этих треугольников находим:
AC12 = AC2 + CC12 и AC2 = AB2 + BC2. Следовательно,
AC12 = AB2 + BC2 + CC12 = AB2 + AD2 + AA21
Следствие. В прямоугольном параллелепипеде все диагонали равны.
set2D(0; 13; 0; 14);
p1 |
= tablePlot( |
11 |
11 |
|
8 |
8 |
|
11 |
8 |
2 |
|
2 |
8 |
11 |
5 |
2 |
); |
||
|
4 |
13 |
|
10 |
1 |
|
4 |
|
1 |
1 |
|
10 |
10 |
13 |
13 |
10 |
|||
p2 |
= tablePlot( |
|
5 |
5 |
2 |
11 |
5 |
11 |
2 |
;0 dash0); |
|
|
|
||||||
13 |
4 |
1 |
4 |
4 |
|
4 |
10 |
|
|
|
|||||||||
p3 |
= pointsPlot( |
11 |
8 |
|
2 |
5 |
11 |
|
8 |
2 |
|
5 |
; |
|
|
|
|
||
4 |
1 |
|
1 |
4 |
13 |
|
10 |
10 |
13 |
|
|
|
|
||||||
[’A’,’B’,’C’,’D’,’A1’,’B1’,’C1’,’D1’],[2,4,4,4,0,0,0,0]); showPlots([p1; p2; p3];0 noAxes0);
15
