с.1.31.38Прямой параллелепипедfigure.1.3 с.1.41.410Пирамидаfigure.1.4

с.2.72.737Прямой параллелепипедfigure.2.7 с.2.82.837Наклонный параллелепипедfigure.2.8

1

Министерство образования и науки Российской Федерации

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ТАМБОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ИМЕНИ Г.Р. ДЕРЖАВИНА»

Кафедра математического анализа

Пример курсовой

работы

Дёмина Станислава Александровича

Научный руководитель

Зав. кафедрой зав.каф., д.ф.м.н.

Тамбов 2015

Оглавление

1.1.1Многогранник . . . . . . . . . . . . . . . . . . . . . . . . . 4

1.1.4Пирамида . . . . . . . . . . . . . . . . . . . . . . . . . . . 8

1.1.5Усеченная Пирамида . . . . . . . . . . . . . . . . . . . . . 11

1.2Свойства граней и диагоналей параллелепипеда . . . . . . . . . 12

1.2.1Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 12

1.2.2Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14

1.3Свойства параллельных сечений в пирамиде . . . . . . . . . . . 16

1.3.1Теоремы . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16

1.3.2Следствие . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

1.3.3Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 18

1.3.4Следствие . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

1.4Боковая поверхность призмы и пирамиды . . . . . . . . . . . . . 21

1.4.1Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21

1.4.2Следствие . . . . . . . . . . . . . . . . . . . . . . . . . . . 22

1.4.3Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

1.4.4Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23

2.0.5Основные допущения в объемах. . . . . . . . . . . . . . . 25

2.0.6Единица объёма. . . . . . . . . . . . . . . . . . . . . . . . 26

2.1Объем параллелепипеда. . . . . . . . . . . . . . . . . . . . . . . . 26

2.1.1Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 26

2.1.2Следствие. . . . . . . . . . . . . . . . . . . . . . . . . . . . 31

2.1.3Лемма . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33

2.1.4Теорема . . . . . . . . . . . . . . . . . . . . . . . . . . . . 34

3

Глава 1

МНОГОГРАННИКИ

1.1ПАРАЛЛЕЛЕПИПЕД И ПИРАМИДА

1.1.1Многогранник

Многогранником называется тело, ограниченное плоскими многоугольниками. Общие стороны смежных многоугольников называются ребрами многогранника. Многоугольники, которые ограничивают многогранник, называются его гранями. Грани многогранника, сходящиеся в одной точке, образуют многогранный угол; вершины таких многогранных углов называются вершинами многогранника. Прямые, соединяющие две какие-нибудь вершины, не лежащие на одной грани, называются диагоналями многогранника. Мы будем рассматривать только выпуклые многогранники, т. е. такие, которые расположены по одну сторону от плоскости каждой из его граней. Наименьшее число граней в многограннике - четыре; такой многогранник получается от пересечения трехгранного угла какой-нибудь плоскостью.

1.1.2Призма

Призмой называется многогранник, у которого две грани - равные многоугольники с соответственно параллельными сторонами, а все остальные грани - параллелограммы. Чтобы показать возможность существования такого многогранника, возьмем (рис. 1.1) какой-нибудь многоугольник ABCDE и через его вершины проведем ряд параллельных прямых, не лежащих в его плоскости. Взяв затем на одной из этих прямых произвольную точку A1, проведем через нее плоскость, параллельную плоскости ABCDE через каждые две соседние параллельные прямые также проведем плоскости. Пересечение всех этих плоскостей определит многогранник ABCDEA1B1C1D1E1, удовлетворяющий определению призмы. Действительно, параллельные плоскости ABCDE и A1B1C1D1 пересекаются боковыми плоскостями по параллельным прямым; поэтому фигуры AA1E1E, EE1D1D и т.д. параллелограммы. С другой стороны, у многоугольников ABCDE и A1B1C1D1 равны соответ-

4

ственно стороны (как противоположные стороны параллелограммов) и углы (как углы с параллельными и одинаково направленными сторонами); следовательно, эти многоугольники равны. Многоугольники ABCDE и A1B1C1D1, лежащие в параллельных плоскостях, называются основаниями призмы, перпендикуляр OO1, опущенный из какой-нибудь точки одного основания на плоскость другого, называется высотой призмы. Параллелограммы AA1B1B и т. д. называются боковыми гранями призмы, а их стороны AA1; BB1 и т. д., соединяющие соответственные вершины оснований, боковыми ребрами. У призмы все боковые ребра равны как отрезки параллельных прямых, заключенные между параллельными плоскостями. Отрезок прямой, соединяющий какие-нибудь две вершины, не прилежащие к одной грани, называется диагональю призмы. Таков, например, отрезок AD1 (рис. 1.1). Плоскость, проведенная через какие-нибудь два боковых ребра, не прилежащих к одной боковой грани призмы (например, через ребра AA1 и CC1 рис. 1.1), называется диагональной плоскостью (на рисунке не показанной). Призма называется прямой или наклонной, смотря по тому, будут ли ее боковые ребра перпендикулярны или наклонны к основаниям. У прямой призмы боковые гранипрямоугольники. За высоту такой призмы можно принять боковое ребро. Прямая призма называется правильной, если ее основания - правильные многоугольники. У такой призмы все боковые грани - равные прямоугольники. Призмы бывают треугольные, четырехугольные и т.д., смотря по тому, что является основанием: треугольник, четырехугольники т. д.

3 3

p4 = tablePlot( 6 22 );

8 8

p5 = tablePlot( 2 4 );

5

showPlots([p1; p2; p3; p4; p5; p6; p7; p8; p9; p10; p11; p12; p13];0 noAxes0);

Рис. 1.1: Многоугольник

1.1.3Параллелепипед

Параллелеп ипе дом называют призму, у которой основаниями служат параллелограммыназывают призму, у которой основаниями служат параллелограммы (рис. 1.2). Параллелепипеды, как и всякие призмы, могут быть прямые и наклонные. Прямой параллелепипед называется прямоугольным, если его основание прямоугольник (рис.1.3). Из этих определений следует:

1) у параллелепипеда все шесть граней параллелограммы;

6

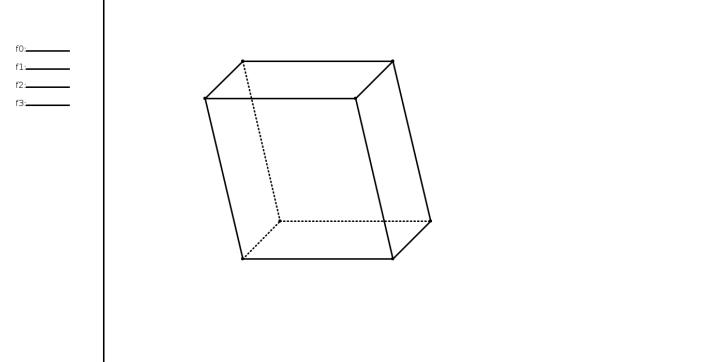
2)у прямого параллелепипеда четыре боковые грани прямоугольники,

адва основания параллелограммы;

3)у прямоугольного параллелепипеда все шесть граней прямоугольни-

ки.

Три ребра прямоугольного параллелепипеда, сходящиеся к одной вершине, называются его измерениями: одно из них можно рассматривать как длину, другое как ширину, а третье как высоту.

Прямоугольный параллелепипед, имеющий равные измерения, называет-

ся кубом. У куба все грани – квадраты.

showPlots([p1; p2; p3; p4];0 noAxes0);

Рис. 1.2: Наклонный параллелепипед

7