p1 = tablePlot( |
4 |
0 |
0 |
16 |
16 |
20 |
20 |
4 |
20 |
20 |
16 |
); |
25 |
21 |
0 |
0 |
21 |
25 |
25 |
25 |
25 |
4 |
0 |
||
p2 = tablePlot( |
0 |
16 |
20 |
); |
|
|
|
|
|
|
|
|
21 |
21 |
25 |
|
|
|
|
|
|
|
|
p3 = tablePlot( |
0 |
4 |
20 |
;0 dash0); |
|
0 |
4 |
4 |
|
p4 = tablePlot( |
4 |
4 |
;0 dash0); |
|
4 |
25 |
|
showPlots([p1; p2; p3; p4];0 noAxes0);
Рис. 1.3: Прямой параллелепипед
1.1.4Пирамида
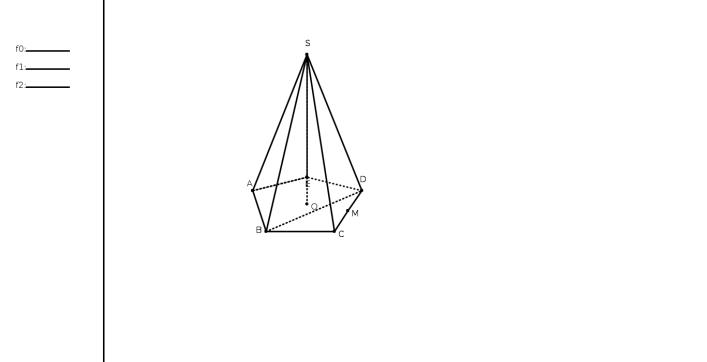
Пирамидой называется многогранник, у которого одна грань, называемая основанием, есть какой-нибудь многоугольник, а все остальные грани, называемые боковыми, треугольники, имеющие общую вершину.
Чтобы получить пирамиду, достаточно какой-нибудь многогранный угол S (1.4) пересечь произвольной плоскостью ABCD и взять отсеченную часть SABCD. Общая вершина S боковых треугольников называется вершиной пирамиды, а перпендикуляр SO, опущенный из вершины на плоскость основания, высотой.
Обыкновенно, обозначая пирамиду буквами, пишут сначала ту, которой обозначена вершина, например SABCD (1.4). Плоскость, проведенная через
9
вершину пирамиды и через какую-нибудь диагональ основания (например, через диагональ BD, 1.6), называется диагональной плоскостью. Пирамиды бывают треугольные, четырехугольные и т.д., смотря по тому, что является основанием треугольник, четырехугольник и т.д. Треугольная пирамида (1.5) называется иначе тетраэдром; все четыре грани у такой пирамиды треугольники. Пирамида называется правильной (1.6), если, во-первых, ее основание есть правильный многоугольник и, во-вторых, высота проходит через центр этого многоугольника. В правильной пирамиде все боковые ребра равны между собой (как наклонные с равными проекциями). Поэтому все боковые грани правильной пирамиды суть равные равнобедренные треугольники. Высота SM (1.6) каждого из этих треугольников называется апофемой. Все апофемы в правильной пирамиде равны.
set2D(0; 11; 0; 11); |
|
|
|
|
|
|
|
|
p1 = tablePlot( |
5 |
1 |
7 |
5 |
8 |
7 |
); |
|
11 |
2 |
2 |
11 |
4 |
2 |
|||
|
0:6 |
1 |
|
|
|
|
|
|
p2 = tablePlot( |
1 |
2 |
|
); |
|
|
|
|
|
8:4 |
8 |
|
|
|
|
||
p3 = tablePlot( |
3 |
4 |
|
); |
|
|
|
|
|
7:2 |
7 |
|
|
|
|
||
p4 = tablePlot( |
1 |
2 |
|
); |
|
|
|
|
|
|
|
|
|
|
|
|
|
p5 = tablePlot( |
1 |
4 |
|
5 |
4 |
8 |
;0 dash0); |
|
|
2 |
4 |
11 |
4 |
4 |
|
|
|
5 |
5 |
|
|
|
|
|
||
p6 = tablePlot( |
11 |
3 |
;0 dash0); |
|
||||
p7 = tablePlot( |
|
: |
4 |
;0 dash0); |
|
|||
338 |
4 |
|
||||||
p8 = pointsPlot( |
1 |
7 |
8 |
4 |
5 |
5 |
; |
|
2 |
2 |
4 |
4 |
11 |
3 |
|||
[0A0;0 B0;0 C0;0 D0;0 S0;0 O0]; [7; 3; 0; 7; 0; 6]); showPlots([p1; p2; p3; p4; p5; p6; p7; p8];0 noAxes0);
set2D(1; 7; 1; 10); |
|
|
|
|
|
|
|
p1 = tablePlot( |
5 |
1 |
2 |
5 |
7 |
2 |
); |
10 |
4 |
1 |
10 |
4 |
1 |
p2 = tablePlot( |
1 |
7 |
;0 dash0); |
|
4 |
4 |
|
p3 = pointsPlot( |
1 |
2 |
7 |
5 |
; [0A0;0 B0;0 C0;0 S0]; [7; 4; 3; 0]); |
|
4 |
1 |
4 |
10 |
|
showPlots([p1; p2; p3];0 noAxes0);
10
Рис. 1.4: Пирамида
Рис. 1.5: Треугольная Пирамида
set2D(2; 10; 1; 15); |
|
|
|
|
|
|
|
|
|
|
p1 = tablePlot( |
3 |
2 |
6 |
10 |
9 |
8 |
6 |
3 |
8 |
); |
2 |
5 |
15 |
5 |
3:5 |
2 |
15 |
2 |
2 |
11
p2 |
= tablePlot( |
3 |
|
10 |
6 |
2 |
6 |
6 |
6 |
;0 dash0); |
||
2 |
|
5 |
6 |
5 |
6 |
15 |
4 |
|||||
p3 |
= pointsPlot( |
2 |
3 |
8 |
9 |
|
10 |
6 |
6 |
6 |
; |
|
5 |
2 |
2 |
3:5 |
5 |
6 |
15 |
4 |
|||||
[0A0;0 B0;0 C0;0 M0;0 D0;0 E0;0 S0;0 O0];
[7; 6; 3; 3; 0; 4; 0; 3]); showPlots([p1; p2; p3];0 noAxes0);
Рис. 1.6: Правильная Пирамида
1.1.5Усеченная Пирамида
Усеченная пирамида. Часть пирамиды (1.7), заключенная между основанием (ABCDE)и секущей плоскостью (A1B1C1D1E1), параллельной основанию, называется усеченной пирамидой. Параллельные грани называются основаниями, а отрезок перпендикуляра OO1, опущенного из какой-нибудь точки O1 основания A1B1C1D1E1 на другое основание, высотой усеченной пирамиды. Усеченная пирамида называется правильной, если она составляет часть правильной пирамиды.
set2D(1; 13; 1; 20); |
|
|
|
|
|
|
|
|
|
|
|
p1 = tablePlot( |
7 |
1 |
4 |
7 |
10 |
4 |
10 |
13 |
7 |
10 |
); |
20 |
6 |
1 |
20 |
1 |
1 |
1 |
6 |
20 |
1 |
12