showPlots([p1; p2; p3; p4; p5; p6; p7];0 noAxes0);

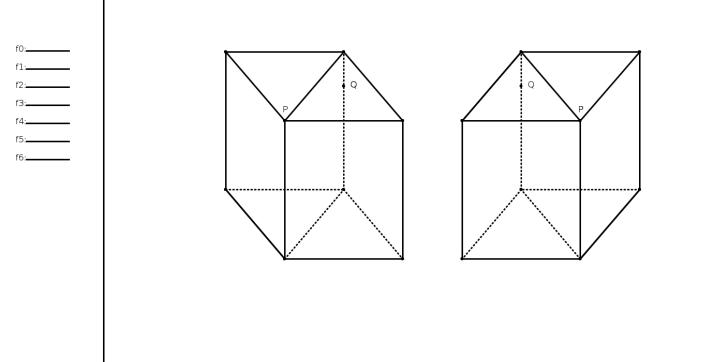
Рис. 2.1: Два параллелепипеда

2.0.6Единица объёма.

За единицу объемов при измерении их берут объем такого куба, у которого каждое ребро равно линейной единице. Так, употребительны кубические метры (m3), кубические сантиметры (cm3) и т.д.

2.1Объем параллелепипеда.

2.1.1Теорема об объеме правильного прямоугольного параллелепипеда

Объем прямоугольного параллелепипеда равен произведению трех его измерений.

В таком кратком выражении теорему эту надо понимать так: число, выражающее объем прямоугольного параллелепипеда в кубической единице, равно произведению чисел, выражающих три его измерения в соответствующей линейной единице, т.е. в единице, являющейся ребром куба, объем которого принят за кубическую единицу. Так, если x есть число, выражающее объем прямоугольного параллелепипеда в кубических сантиметрах, и a; b и c

31

числа, выражающие три его измерения в линейных сантиметрах, то теорема утверждает, что x = abc При доказательстве рассмотрим особо следующие три случая: 1) Измерения выражаются целыми числами. Пусть, например, измерения, будут (2.2) AB = a; BC = b и BD = c, где a; b и c какие-нибудь целые числа (например, как изображено у нас на рисунке: a = 4; b = 2 и c = 5). Тогда основание параллелепипеда содержит ab таких квадратов, из которых каждый представляет собой соответствующую квадратную единицу. На каждом из этих квадратов, очевидно, можно поместить по одной кубической единице. Тогда получится слой (изображенный на 2.2), состоящий из ab кубических единиц. Так как высота этого слоя равна одной линейной единице, а высота всего параллелепипеда содержит c таких единиц, то внутри параллелепипеда можно поместить c таких слоев. Следовательно, объем этого параллелепипеда равен abc кубических единиц. 2) Измерения выражаются дробными числами. Пусть измерения параллелепипеда будут:

mn ; pq ; rs

(некоторые из этих дробей могут равняться целому числу). Приведя дроби к одинаковому знаменателю, будем иметь:

mqsngs ; pnsqns; rnqsnq:

Примем nqs1 долю линейной единицы за новую (вспомогательную) едини-

цу длины. Тогда в этой новой единице измерения данного параллелепипеда выразятся целыми числами, а именно:

(mqs) (pns) (rnq);

и потому по доказанному (в случае 1) объем параллелепипеда равен произведению (mqs) (pns) (rnq), если измерять этот объем новой кубической единицей, соответствующей новой линейной единице. Таких кубических еди-

ниц в одной кубической единице, соответствующей прежней линейной едини- q

це, содержится (nqs)3; значит, новая кубическая единица составляет (nqs)3

прежней. Поэтому объем параллелепипеда, выраженный в прежних единицах, равен

3) Измерения выражаются иррациональными числами. Пусть у данного параллелепипеда (2.3), который для краткости мы обозначим одной буквой Q, измерения будут:

AB = ; AC = ; AD = ;

32

где все числа ; и или только некоторые из них иррациональные. Каждое из чисел ; и может быть представлено в виде бесконечной десятичной дроби. Возьмем приближенные значения этих дробей с n десятичными знаками сначала с недостатком, а затем с избытком. Значения с недостатком обозначим n; n; n значения с избытком n0 ; n0 ; n0 . Отложим на ребре AB, начиная от точки A, два отрезка AB1 = n и AB2 = n0 . На ребре AC от той же точки A отложим отрезки AC1 = n и AC2 = n0 и на ребре AD от той же точки отрезки AD1 = n и n0 . При этом мы будем иметь

AB1 < AB < AB2; AC1 < AC < AC2; AD1 < AD < AD2:

Построим теперь два вспомогательных параллелепипеда: один (обозначим его Q1) с измерениями AB1; AC1 и AD1 и другой (обозначим его Q2) с измерениями AB2; AC2 и AD2. Параллелепипед Q1 будет весь помещаться внутри параллелепипеда Q, а параллелепипед Q2 будет содержать внутри себя параллелепипед Q. По доказанному (в случае 2) будем иметь:

Q1 = n n n; (1)

Q2 = n0 n0 n0 ; (2)

причем объем Q1 < объема Q2.

Начнем теперь увеличивать число n. Это значит, что мы берем приближенные значения чисел ; ; gamma все с большей и большей степенью точности. Посмотрим, как при этом изменяются объемы параллелепипедов Q1

иQ2 При неограниченном возрастании n объём Q1, очевидно, увеличивается

ив силу равенства (1) при беспредельном увеличении n имеет своим пре-

делом предел произведения( n; n; n). Объем Q2, очевидно уменьшается и

в силу равенства (2) имеет пределом предел произведения n0 ; n0 ; n0 . Но из алгебры известно, что оба произведения n; n; n и n0 ; n0 ; n0 при неограниченном увеличении п имеют общий предел, который является произведением иррациональных чисел Этот предел мы и принимаем за меру объема параллелепипеда Q: объём Q = . Можно доказать, что определенный таким образом объем удовлетворяет тем условиям, которые установлены для объема. В самом деле, при таком определении объема равные параллелепипеды, очевидно, имеют равные объемы. Следовательно, первое условие выполняется. Разобьем теперь данный параллелепипед Q плоскостью, параллельной его основанию, надвое: Q1 и Q2 (2.4). Тогда будем иметь:

Q1 = AB AC AD;

Q2 = AB AA1 AD;

Q3 = A1B1 A1C A1D1:

33

Складывая почленно два последних равенства и замечая, что A1B1 = AB и A1D1 = AD, получим объем Q1 + объем Q2 = AB AA1 AD + AB A1C AD = AB AD(AA1 + A1C) = AB AD AC, отсюда получаем:

Q1 + Q2 = Q:

Следовательно, и второе условие тоже выполняется, если параллелепипед складывать из двух частей, полученных разрезанием его плоскостью, параллельной одной из граней.

34

Рис. 2.2: Параллелепипед

35